,
где 
- оптическая толща как вклад молекулярного поглощения;
- оптическая толща как вклад аэрозольного поглощения;
n(h) - концентрация газа;
- коэффициент поглощения;
- оптическая толща.
Нейронная сеть строится таким образом, что в качестве входа служат значения оптической толщи на каждой высоте, а выходом служат значения концентрации. При этом удобно использовать сеть типа многослойный персептрон.
В данной работе предлагается алгоритм настройки многослойной нейронной сети, основанный на матрично-векторных преобразованиях, для решения задачи лидарного зондирования. Если вход и выход нейронной сети представить в виде векторов, а весовые коэффициенты в виде матрицы, то связь входа нейронной сети с ее выходом можно представить в виде следующего выражения:
,
где, Y - матрица выходных обучающих примеров;
FK - вектор активационных функций K- го слоя;
WK - матрица весовых коэффициентов K- го слоя;
X - матрица входных обучающих примеров.
Во входных и выходных матрицах обучающие примеры расположены в столбцах матрицы, каждая строка матрицы весовых коэффициентов принадлежит одному нейрону. Алгоритм заключается в выражении матриц коэффициентов через входную, выходную матрицы и активационные функции. Для однослойной сети данные выражения можно получить следующим образом:
, 
,
где F-1 - функция обратная к активационной функции.
Например, для активационной функции 
активационная функция это 
, а для 
это 
.
Далее умножаем справа на транспонированную матрицу входных примеров,
,
.
Алгоритм вычисления весовых матриц для многослойных сетей можно определить следующим образом:
,
,
где 
;
;
;
;
.
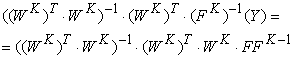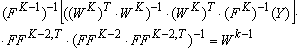Обозначим псевдо-обратные матрицы в виде:
,
.
Используя эти псевдо-обратные матрицы, получаем итерационные формулы (1). Элементы матрицы весовых коэффициентов сначала задаются случайным образом. Затем на основе входной, выходной матриц, а также на основе 1,..., K-1 весовых матриц вычисляется матрица WK. Затем, используя новую матрицу WK, вычисляется матрица WK-1 и т.д. для остальных слоев нейронной сети:
,
, (1)
.
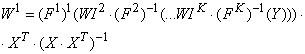Уточняя последовательно весовые матрицы, можно получить исходное решение. Было проведено тестирование метода, для двухслойной и однослойной нейронных сетей. Точность восстановления параметров для однослойной нейронной сети составляет 2-3 %, для двухслойной 1-2 %.
Достоинство алгоритма в том, что он обладает большей по сравнению с другими алгоритмами скоростью, но при этом возможны сложности с вычислением псевдо-обратных матриц, в этом случае необходимо прибегнуть к различным методам регуляризации. Также можно в обучающие матрицы ввести слабый шум. Для обучения сети данным методом рекомендуется выбирать линейно-независимые обучающие примеры во входных и выходных выборках. Также для нейронных сетей с большим числом слоев необходимо увеличивать регуляризирующий параметр. Начальные значения матриц весовых коэффициентов рекомендуется задать случайным образом с распределением, соответствующим обратной активационной функции.