Система координат выбрана так, что невозмущённая поверхность жидкости совпадает с плоскостью z* = 0, а жидкость занимает область z* < 0. Ось z* направлена против вектора g→*, ось x* совпадает с направлением распространения волны.
Система уравнений движения жидкости и электрического поля вне проводящей жидкости имеет вид [1,2]:
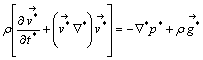(1)
div* v→ * = 0, rot* E→ *= 0, div* D→* =0,
где ρ - плотность, v→ *- скорость, р*- давление, g→* - ускорение силы тяжести,
, 
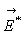- напряжённость электрического поля, ε = const - диэлектрическая проницаемость газа.
Из (1) следует 
где φ* - электрический потенциал. При наличии волны можно записать
, 
, 
где 
Граничные условия на твёрдых поверхностях (обкладках конденсатора) и на свободной поверхности жидкости z*=ξ*(x*,t*):
1) vz * = 0 при z*=-h1* ; 2) 
= 
,
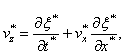
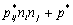где 
при z*=ξ*(x*,t*);
3) φw* при z*= h2*. Здесь pa* - давление в атмосфере; n→ - вектор нормали к поверхности жидкости, направленный из области 1 в - 2.
Поверхностная плотность электрического заряда находится из равенства 
.
Примем, что все величины зависят от x* , t* через x* -с t*, где с - фазовая скорость. В качестве малого параметра примем 
, где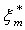 
- максимальное смещение поверхности, 
- волновое число, λ - заданная длина волны.
Вводя безразмерные величины:
х = k(x* - ct*), z = kz*,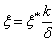 
, 
,
, 
, 
, 
, 
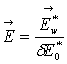, запишем уравнение движения (1) в безразмерном виде:
,
;
,
,
где 
- векторы осей x, z.
Граничные условия в безразмерном виде:
1) vz = 0 (z = -h1);
2) 
, 
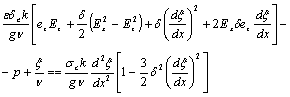
(z = δξ(x)); (2)
3) E→ = 0, φ = 0, (z=h2); где 
,
, 
, 
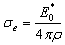Следует добавить также условия периодичности и симметрии волны относительно вертикали, проходящей через вершину волны.
Таким образом, имеем нелинейную краевую задачу для нахождения величин 
, решение которой ищем в виде рядов по малому параметру: 
;
;
;
;
;
;
, (3)
где n - натуральное число.
В граничных условиях (2) все величины следует разложить в ряд Тейлора в окрестности невозмущённой поверхности z = 0. Подставляя ряды (3) в уравнения и граничные условия (2) и приравнивая коэффициенты при одинаковых степенях δ, получим систему уравнений для нахождения первого, второго и третьего приближений. Для нахождения последовательных приближений запишем величины vzj , Exj , Ezj (j = 0;1;2) во всех приближениях в виде рядов по нормированным собственным функциям линейной задачи, соответствующей параметру δ = 0:
, 
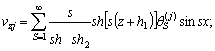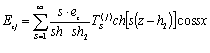
где j=0, 1, 2, 3, ...
Здесь 
- неизвестные коэффициенты.
В первом (линейном) приближении получим:
;
;
;
;
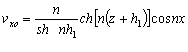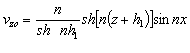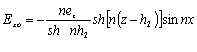ξo=cos nx;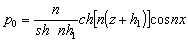 
.
Аналогично находятся второе и третье приближения. Собирая вместе все три приближения окончательно запишем решение задачи с точностью до третьего приближения включительно:
;
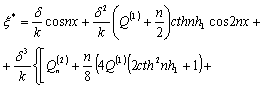
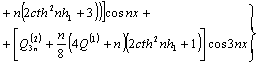
; (4)
;
;
,
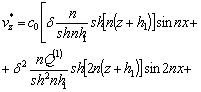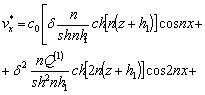
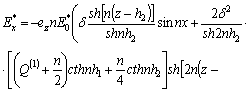
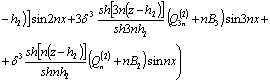
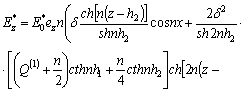
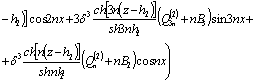где 
= 
, 
,
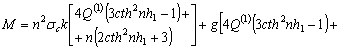
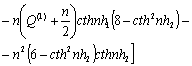
N = g+σckn2 - εσekn 
; Q(1) =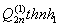
;
;
;
;
K1=3g(cth2nh1 - 1) + 3n2kσc(3cth2nh1 - 1) + nεσek{(3 - cth2nh1) (cthnh1 + cthnh2) - 2(cthnh2 + 2)cth2nh2·cth2nh1};
L1 = g + kn2σc(1 - 3cth2nh1) + nεσek(cth2nh1 - 1)cthnh2;
, 
,
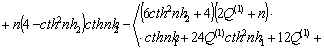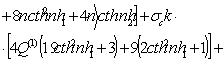
L2= 4(3σckn2cth2nh1 - g).
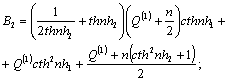
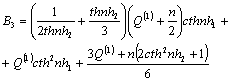
На рис.1 приведён график зависимости частоты ω от E0* при δ=0,1, g=981 см/с2 ; h1*=5 см, h2*=5 см и различных значениях λ для жидкого натрия при температуре С, имеющего следующие значения параметров: ρ = 0,9 г/см3, α = 200 дин/см . При увеличении λ графики «сжимаются» вдоль оси ω и «вытягиваются» вдоль оси E0*. Для каждого значения λ существует значение E0*, при котором ω = 0. Чем меньше λ, тем круче «опускается» график с ростом E0*. Для всех длин волн величина ω достигает максимума при E0*= 0. Таким образом, электрическое поле уменьшает частоту волны.
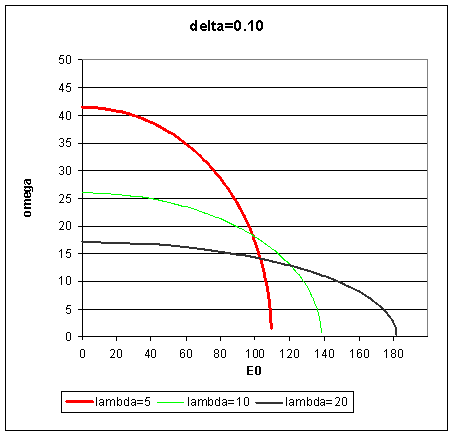
Рисунок 2. Зависимость частоты ω от E0*
На рис.2 изображён график зависимости 
на интервале 
(по оси абсцисс отложены значения x, а по оси ординат значения ξ) при k = 2 см -1, E0*= 40 единиц СГС, h1*= 3см, h2*=5см, δ =0,1. Амплитуда ξ (x) при x = ± 1,486. Единица измерения E* в системе CГС равна 300 В/см. Отметим, что электрический пробой воздуха наступает примерно при E*0 = 30 кВ/см.
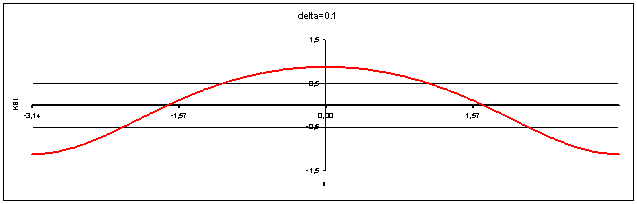
Рисунок 2. График зависимости ξ(x) на интервале
Рассмотрим частный случай, когда толщина слоя жидкости мала 
, т. е. длина волны велика, а область 2, занятая газом, имеет большую толщину 
. Выражение для фазовой скорости имеет вид: 
, где
А - некоторый параметр, зависящий от величин k,h1 ,h2 , α, g,E0* , ρ.
При отсутствии электрического поля и поверхностного натяжения выражение для фазовой скорости совпадает с известным выражением в обычной гидродинамике [3]. В линейном приближении δ = 0 фазовая скорость равна 
. При 
, когда 
получим выражение для высоты волны [3]:
, где 
.
Если 
, , то 
.
Для исследования полученных результатов введём два безразмерных параметра взаимодействия, характеризующих относительную величину капиллярных и электрических сил по сравнению с гравитационными 
, 
Смещение точек свободной поверхности жидкости (4) запишем в виде (n=1):
,(5)
, 
, 
,
,
,
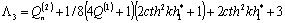
Отметим, что выражение (5) неприменимо при 
, 
При 
(гравитационная волна) выражение (5) совпадает с полученным в [3] 
.
Выражение для высоты волны (расстояние по вертикали от впадины при х = π до уровня вершины) при х = 0 имеет вид:
, (6)
Рассмотрим далее частный случай: 
Коэффициенты в выражение (5) в этом случае примут вид:
,
,
Отметим, что выражение (5) неприменимо при ПЕ - Пс = 1, ПЕ = =3Пс. При отсутствие поверхностного натяжения Пс = 0 (0 < ПЕ < <1), получим 
. Откуда видно, что амплитуда волны зависит линейно от величины ПЕ.
СПИСОК ЛИТЕРАТУРЫ
- Ландау Л.Д., Лифшиц Е.М. Гидродинамика. - М.: Наука, 1986. - 735 с.
- Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. - М.: Наука, 1982. - 624 с.
- Алешков Ю.З. Теория волн на поверхности тяжёлой жидкости. - Л.: Изд-во Ленингр. ун-та, 1981. - 196 с.