Низкоамплитудные электрические сигналы являющиеся ответом головного мозга на какое-либо внешнее раздражение принято называть вызванными потенциалами (ВП). В качестве раздражителя могут выступать световые вспышки, звуковые сигналы, а также стимулирование нервных окончаний электрическим током. На основе анализа формы низкоамплитудных электрических сигналов, амплитудных и временных параметров возможна диагностика тяжёлых патологий и заболеваний головного мозга человека.
Согласно исследованиям реализации ВП являются нестационарным случайным процессом с гауссовской плотностью распределения. Помехами, на фоне которых осуществляется регистрация ВП, являются шумы измерения и сигналы спонтанной активности головного мозга - электроэнцефалограмма. Помехи также можно представить в виде случайного стационарного процесса с гауссовской плотностью распределения.
При построении модели принимается допущение, что характер воздействия помехи на сигнал является аддитивным. Исходя из этого ВП можно представить односвязным марковским случайным процессом с гауссовской плотностью распределения. Так как современные медицинские системы осуществляют регистрацию и обработку сигналов по многим отведениям одновременно, выделяемый сигнал целесообразно представить векторной моделью. В этом случае модель выделяемого сигнала в матричном виде можно представить двумя уравнениями: уравнением сообщения:
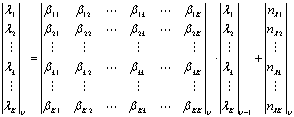 (1)
(1)
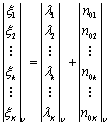
и уравнением наблюдения:
 ,
, ![]() , (2)
, (2)
где β ij - коэффициенты матрицы , имеющей размерность (К x К) (К - количество каналов измерения), определяющие взаимосвязи между каналами;λ kv - элементы вектора столбца, определяющего значения реализации ВП; n0kv - элементы вектора столбца, задающего последовательность аддитивного независимого гауссовского шума возникающего при регистрации ВП; nλkv - элементы вектора столбца, задающего последовательность формирующего независимого гауссовского шума, V - количество отсчётов в реализации. При этом, функциональные связи задаются с помощью матрицы B v-1, а вариабельность сигналов вектором формирующего шума. Диагональные элементы матрицы B v-1 определяют взаимосвязи между отсчётами реализации одного канала, а недиагональные элементы определяют взаимосвязи между отсчётами разных каналов.
Основной проблемой при разработке векторной модели является определение неизвестных коэффициентов βij . Решение системы уравнений (1) с целью нахождения коэффициентов невозможно из-за недостаточного количества уравнений. Поэтому была разработана методика определения коэффициентов матрицы B v-1, основанная на положении о том, что для множества пациентов матрица коэффициентов взаимосвязей является постоянной, а индивидуальную особенность реализаций ВП отдельного человека задаётся вектором формирующего шума nλv. В этом случае, в системе (1), количество уравнений увеличивается, а количество неизвестных остаётся прежним.
Был разработан алгоритм вычисления коэффициентов взаимосвязей векторной модели ВП. На основе алгоритма разработан программный продукт. В ходе исследования были вычислены коэффициенты матрицы B v-1. Также были вычислены и оптимизированы по критерию минимума среднего квадрата ошибки значения вектора столбца формирующего шума n λv. Адекватность модели определялась путём формирования реализаций на основе систем (1) и (2) с использованием вычисленных значений коэффициентов матрицы B v-1 и вектора n λv. Анализ показал, что ошибка аппроксимации реального ВП не превышала 10%.
Решение задачи идентификации модели низкоамплитудных электрических сигналов головного мозга позволит разработать эффективные методы выделения ВП из шумов, что повысит качество обработки и достоверность диагностики


