Трибологические свойства поверхности композиционных покрытий (КП) существенно зависят от конфигурации межфазных границ [1-4]. Интерпретация этого влияния в рамках синергической модели [5] основана на предположении о квазифрактальном характере этих конфигураций. Анализ возможности поиска поверхностных фрактальных структур с необходимыми характеристиками как вероятных аппроксимантов конфигураций межфазных границ является задачей данной работы. При формировании подобных фрактальных структур методами модулярного дизайна использовали теоретические положения, изложенные в работах [6-19].
Фрактальная кривая n-го поколения, сформированная итерацией генератора G = LK(1/l) на отрезке – стороне многоугольника {Pg} = {N}, может быть представлена как F{Pg},n = FK(1/l){Pg}n(G22){1+} [13-16]. Здесь: K – коэффициент самоподобия, n – количество итераций (значение n = 0 соответствует исходному многоугольнику, n =1 – генератору), G22 – симметрия фигуры, образованной замкнутой фрактальной кривой, 1+ означает, что ее размерность превышает топологическую размерность 1 инициального отрезка прямой.
Множества замкнутых фрактальных кривых МFK(4/3){Pg}(G22), построенные на периметре {N}-тел (темных {Pg} – ячеек некоторых сеток Кеплера-Шубникова), образуют совокупности фигур, представляющие собой упаковки определенных снежинок Коха в 2D-пространстве [16]. Множества замкнутых фрактальных кривых MF-K (4/3) Σ{Pg}(G22), построенные на периметре {N}-лакун (светлых {Pg}), образуют совокупность лакунарных фигур, дополняющие соответствующие множества МFK(4/3){Pg}(G22) до 2D-пространства [16]. В случае треугольных лакун генерируемое множество лакунарных кривых представляет собой результат его расслоения на мультимножество кривых МFK(4/3) Σ{3}(G22), каждая из которых состоит из определенного множества самоподобных с К(2/9) замкнутых кривых в виде двух сросшихся с частичным наложением снежинок Коха FK(4/3){3}(p6mm) [16].
Для формирования фрактальных кривых можно использовать треугольные генераторы Коха гомологических рядов К(2(n+1)/(n+2)) (а) и К(2(3n-1)/3n) (б) (рис. 1, слева) [20]. В результате итерации данных генераторов на периметрах {n}-тел сеток Кеплера-Шубникова образуется множество разнообразных снежинок Коха, упорядоченных в 2D-пространстве [16].
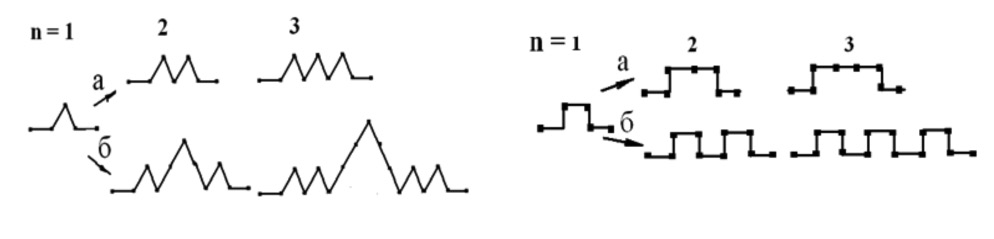
Рис. 1. Изображения первых трех членов гомологических рядов треугольных генераторов Коха К(2(n+1)/(n+2)) (а) и К(2(3n-1)/3n) (б) и прямоугольных генераторов Коха К((n+4)/(n+2)) (а) и К((4n+1)/(2n+1)) (б)
По мере увеличения порядкового номера генератора в каждом гомологическом ряду при итерации наблюдается закономерное увеличение длины квазифрактальной кривой и изменение ее размерности в соответствии с зависимостями D = ln2(n+1)/ln(n+2) и D = ln2(3n–1)/ln3n [20].
Рассмотрим и некоторые другие виды генераторов. Бесконечная итерация прямоугольных генераторов G, в том числе и видоизмененной кривой Коха K(5/3)), на отрезке конечной длины приводит к формированию бесконечной фрактальной линии. Для моделирования могут быть использованы некоторые из сеток Кеплера-Шубникова, которые включают в себя тетрагоны {4} – ячейки сеток и являются производными от сеток Кеплера 4444, 488 или 46.12. Прямоугольный генератор К(5/3) является первым членом двух гомологических рядов прямоугольных генераторов К((n+4)/(n+2)) и К((4n+1)/(2n+1)), где n = 1,2,3…∞ (см. рис. 1, справа) [21]. Размерности фрактальных кривых, образованных с помощью генераторов К((n+4)/(n+2)) и К((4n+1)/(2n+1)), могут быть представлены как D = ln(n+4)/ln(n+2) и D = ln(4n+1)/ln(2n+1) [21]. При n→∞ величины D закономерно уменьшаются от 1,465 до значения 1,001.
Прямоугольный генератор-меандр К(8/4) является первым членом двух гомологических рядов меандров вида ((6n+2)/(2n+2)) и К((10n-2)/(2n+2)), где n = 1,2,3…∞ (рис. 2, слева) [22]. При многократном действии генераторов K((6n+2)/(2n+2)) на периметр ячейки квадратной сетки Кеплера 4444 формируется упорядоченное множество предфрактальных кривых. Для каждой замкнутой фрактальной кривой в ряду K((6n+2)/(2n+2)) размерность D = ln(6n+2)/ln(2n+2) при n→∞ закономерно уменьшается от 1,500 до 1,001 (рис. 3) [22]. При действии генераторов К((10n–2)/(2n+2)) на периметр ячейки квадратной сетки Кеплера 4444 формируется упорядоченное множество предфрактальных кривых. В гомологическом ряду генераторов К((10n–2)/(2n+2)) размерность каждой фрактальной кривой D = ln(10n–2)/ln(2n+2) принимает максимальное значение 1,613 при n = 2, а затем при n→∞ закономерно уменьшается также до значения 1,001 (рис. 3) [22].
Генератор К(6/2) является первым членом как минимум двух разновидностей гомологических рядов меандроподобных генераторов К(6n/2n) (см. рис. 2, справа) [23]. По мере увеличения порядкового номера генератора в каждом гомологическом ряду при итерации наблюдается закономерное изменение ее хаусдорфовой размерности D в соответствии с зависимостью D = ln6n/ln2n [23]. Фрактальная размерность кривой максимальна для первого члена данного ряда, а начиная со вторых членов ряда в представлениях (а) и (б) (рис. 2) размерности кривых D < 2 и при n→∞ закономерно уменьшаются от 1,792 до 1,001 (рис. 3) [23].
Таким образом, в 2D-пространстве могут быть сформированы фрактальные структуры вида МFK(1/l){Pg}{1+}. Данные фрактальные структуры характеризуются размерностями практически во всем диапазоне значений в интервале от 1 до 2 и могут быть использованы для интерпретации результатов исследований трибологических свойств поверхности композиционных материалов и покрытий [1-4, 24-27].
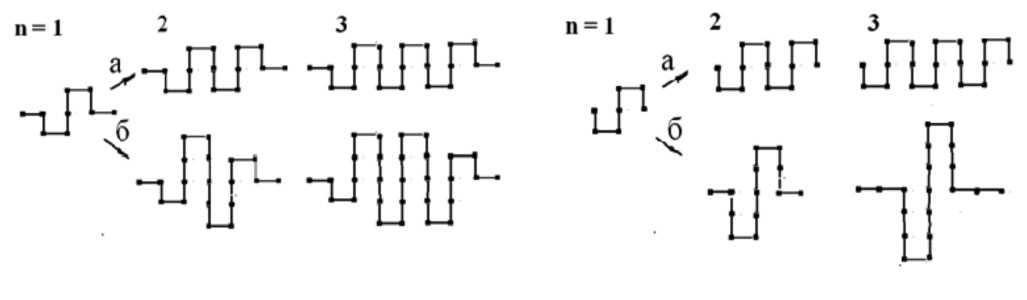
Рис. 2. Изображения первых трех членов гомологических рядов меандров K((6n+2)/(2n+2)) (а) и К((10n-2)/(2n+2)) (б) и гомологического ряда меандроподобных генераторов Коха К(6n/2n) (а и б)
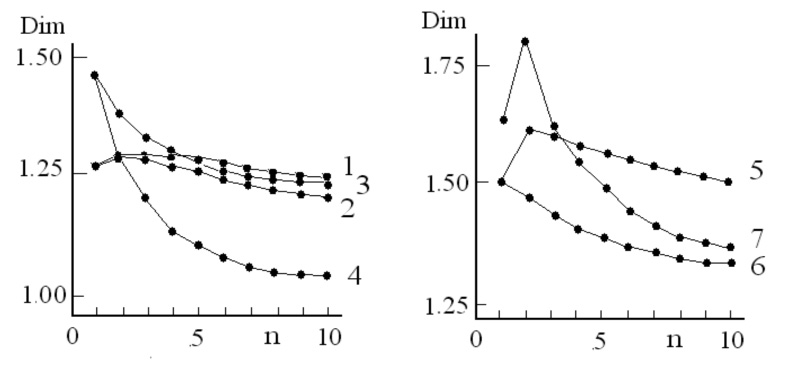
Рис. 3. Изменение размерности фрактальных структур вида FK(1/l){Pg}n(G22){1+} от порядкового номера n в гомологических рядах инициирующих генераторов К(2(n+1)/(n+2)) (1), К(2(3n-1)/3n) (2), К((4n+1)/(2n+1)) (3), К((n+4)/(n+2)) (4), К((10n-2)/(2n+2)) (5), K((6n+2)/(2n+2)) (6), и К(6n/2n (7)
Работа выполнена при финансовой поддержке Министерства образования и науки РФ, соглашение № 14.U01.21.1078.
Библиографическая ссылка
Дерлугян П.Д., Иванов В.В., Иванова И.В., Шишка В.Г., Дерлугян Ф.П., Бережной Ю.М. ФОРМИРОВАНИЕ ЛИНЕЙЧАТЫХ ФРАКТАЛЬНЫХ СТРУКТУР С НЕОБХОДИМЫМИ ХАРАКТЕРИСТИКАМИ В 2D-ПРОСТРАНСТВЕ // Современные наукоемкие технологии. 2013. № 10-1. С. 158-160;URL: https://top-technologies.ru/ru/article/view?id=33401 (дата обращения: 11.07.2025).



