Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Еременко Ю.И. Уварова Л.В.

Статья в формате PDF

183 KB

Методы построения автоматических систем управления, как правило, основаны на использовании строгих математических моделей объекта. Однако, для определенной части объектов управления, построение точных математических моделей практически невозможно ввиду плохой формализуемости, к тому же, эти объекты могут функционировать в среде, свойства которых изменяются или вообще не могут быть определены заранее. К таким объектам можно отнести станции систем водоотведения, так как процессы водоотведения являются производными, как от процессов водопотребления, так и от процессов образования атмосферных осадков и аварийных подтоплений. В этих условиях зачастую неприемлемы традиционные детерминированные и статистические подходы к построению и идентификации математических моделей. Один из перспективных путей преодоления отмеченных трудностей заключается в привлечении качественной информации в виде словесного описания при сборе и оценке измеряемых параметров, анализе связей и принятия решений. При построении математической модели качественную информацию, заданную набором терминов, необходимо формализовать, т.е. представить в виде математических объектов.

В условиях нашего применения сосредоточим основное внимание на нечеткой разностной модели, построенной на базе нечетких моделей Такаги (Takagi), Сугено (Sugeno), Канга (Kang) и именуемой TSK  моделью [4].

При построении нечеткой разностной TSK-модели необходимо учитывать следующие условия работы насосной станции водоотведения [3]:

Запишем продукционные правила нечеткой динамической модели с обратной связью, для которой не требуется знание выхода y(t - 1),..., y(t - r) на .

R^q: если (t - 1) есть Y₁^θ,..., (t - r) есть Y_r^θ, u(t) есть U₁^θ,..., u(t -s) есть U_s^θ, то

,                                      (1)

где ŷ(t - 1), ..., ŷ(t - r) - рассчитанные по нечёткой модели значения выхода в моменты времени t - 1, ..., t - r.

Введем новые обозначения переменных  , образующих входной вектор

,

нечетких множеств и коэффициентов линейных уравнений , позволяющие переписать (1) в более компактном виде

R^q: если x₁(t) есть X₁^θ(t),..., x_m(t) есть X_m^θ, то

                                                             (2)

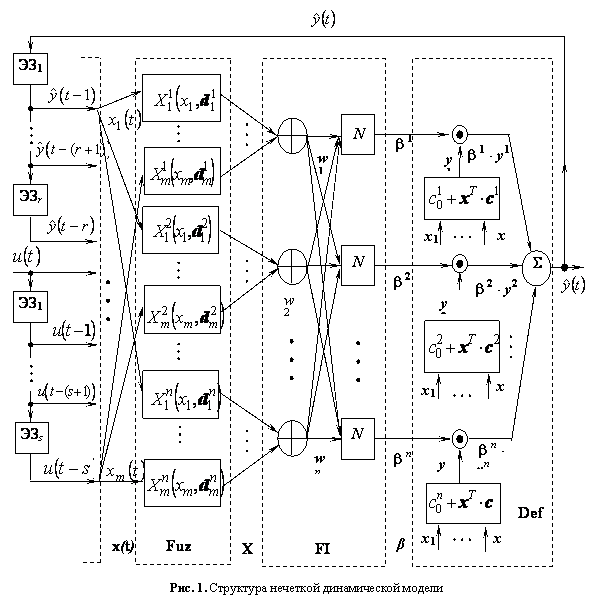
Нечёткие множества в правилах (2) имеют соответствующие функции принадлежности . На рис. 1 показана структура нечеткой модели с обратной связью, оснащенная элементами запаздывания ЭЗ_l на l тактов l =1,2,... и процедурами фазификации, нечеткого вывода и дефазификации [1,2].

В блоке фазификации Fuz (Fuzzyfication) значения переменных x₁(t),..., x_m(t) преобразуются в матрицу 

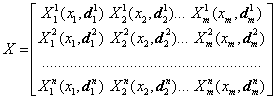
с элементами , представляющими результаты расчета соответствующих функций принадлежности при задании переменных x_i и параметров d_i^θ .

В блоке нечеткого вывода FI (Fuzzy Inference) вычисляется величина истинности q - го правила

и нечеткая функция

,

где операция алгебраического умножения (×), определения максимума (max) или минимума (min) и др.

В блоке дефазификации Def (Defuzzyfication) определяется конкретное значение выхода по формуле

,                                                                   (3)

где - разностное уравнение; - вектор коэффициентов.

В качестве выражения, реализующего нечеткий вывод, целесообразно использовать произведение Ларсена

,                                             (4)

сохраняющее непрерывность нечеткой TSK - модели относительно параметров функций принадлежности.

Продолжая преобразования, заменим y^θ(t) на

,                                                              (5)

где - вектор коэффициентов линейного уравнения q - го правила; - расширенный входной вектор q - го правила, содержащий нелинейную нечеткую функцию b^q(t, d ^q).

Таким образом, формула (3) - является аналитическим выражением TSK - модели со структурой учитывающей условия работы насосной станции водоотведения, изображенной на рис. 1.

По аналогии с (1) нечеткую разностную TSK - модель динамики гидравлических процессов насосной станции водоотведения запишем в виде продукционных правил, которые определяют выход(t): 

              (6)

Нечеткие множества Y_i^θ характеризуются колоколообразными функциями принадлежности , зависящими от шести компонентов вектора d_i^θ. Входные управляющие переменные u_i(t-l) принимают два значения 0 или 1 и действуют с запаздыванием Величина порядка r, должна быть ограниченной, в противном случае резко возрастает размер правил и, соответственно, объем, и громоздкость вычислений.

СПИСОК ЛИТЕРАТУРЫ

1. Кудинов Ю.И., Венков А.Г., Келина А.Ю. Моделирование технологических и экологических процессов (монография). - Липецк: ЛЭГИ, 2001. - 131 с.

2. Кудинов Ю.И., Венков А.Г., Тянуто-
ва С.А., Кудинова Л.И. Построение нечеткой динамической модели // Сборник научных трудов Международного научно-практического семинара «Интегрированные модели и мягкие вычисления в искусственном интеллекте». - М.: Наука, 2001. - С. 293 - 298.

3. Лезнов Б.С. Энергосбережение и регулируемый привод в насосных и воздуходувных установках. - М.: Энергоатомиздат,2006. 360 с. ил.

4. Takagi T., Sugeno M. Fuzzy identification of systems and its applications to modeling and control // IEEE Transactions on Systems Man and Cybernetics, 1985. - V. SMC - 15. - P. 116-132.

Библиографическая ссылка