Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы

Курамшина А.Е. Бочкор С.А. Кузнецов В.В.

Результаты исследования маршрутов конформационной изомеризации 1,3-диоксана и тетрагидро-1,3-оксазина в присутствии молекулы гексапептида с помощью расчетного метода АМ1 свидетельствуют о заметном влиянии биомолекулы на конформационную изомеризацию, проявляющемся в снижении различий в энергии между конформерами кресла и 1,4-твист-, а также в стабилизации отдельных форм, соответствующих локальным максимумам на поверхности потенциальной энергии молекул исследованных 1,3-гетероциклов.

Статья в формате PDF

183 KB

  Введение

Интерес к кислород- и азотсодержащим гетероаналогам циклогексана обусловлен все более возрастающим значением этих соединений в тонком органическом синтезе (получение энантиомерных спиртов и полиенов, аминоспиртов, эффективных катализаторов), а также комплексом практически полезных свойств (биологически активные вещества, ингибиторы коррозии, компоненты полимерных и горюче-смазочных материалов [1,2]) и особенностями строения (электронные и стерические внутримолекулярные взаимодействия). В частности, замещенные 1,3-диоксаны и тетрагидро-1,3-оксазины используются в качестве гербицидов, стимуляторов роста, инсектицидов, репеллентов, зооцидов, фунгицидов и бактерицидов. Наличие антимикробной и противовоспалительной активности позволяет применять их в косметических препаратах и медицине. Последняя область представляет особый интерес из-за разнообразия обнаруженных фармакологических свойств: нейролептических, антигистаминных и спазмолитических, расширяющих коронарные сосуды, гипогликемических, анестезирующих и антихолинергических. Обсуждаемые соединения оказывают также анальгетическое, бронхорасширяющее и противоязвенное, антиконвульсивное и противоопухолевое, противозачаточное действия, могут использоваться также для лечения сердечной недостаточности, гипертонии, ожирения, при грибных отравлениях [1].

Однако надежное конформационное отнесение молекул рассматриваемых соединений, невзирая на большое число публикаций, в ряде случаев остается проблематичным, а порой и вовсе невозможным из-за неоднозначного понимания результатов эксперимента и противоречивых концепций, описывающих их конформационную динамику. Совершенно не исследовано и влияние на конформационные свойства обсуждаемых гетероциклов достаточно большой биомолекулы в системе "биологически активный субстрат - рецептор". Между тем знание основных принципов построения поверхности потенциальной энергии таких систем может объективно помочь в понимании тонких особенностей механизма действия лекарственных препаратов на их основе. В этой связи выявление основных закономерностей конформационной динамики 1,3 - диоксанов и тетрагидро-1,3 - оксазинов, а также моделирование взаимодействия молекул этих веществ с рецепторами остается очень важной и актуальной проблемой.

1. Моделирование поверхности потенциальной энергии изолированных молекул 1,3-диоксанов и тетрагидро-1,3-оксазинов

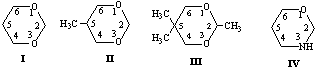
Нами с помощью эмпирического (ММ+), а также полуэмпирических и неэмпирических методов в рамках программного обеспечения HyperChem [3] исследована поверхность потенциальной энергии (ППЭ) молекул 1,3-диоксанов (I-III) и тетрагидро-1,3-оксазина (IV). Известно, что главному минимуму на ППЭ 1,3-диоксанов и тетрагидро-1,3-оксазинов отвечает конформер кресла, К (в случае соединения II - c преимущественно аксиальной ориентацией N-H протона, NHa)[4-7].

Методом ММ+ при использовании в качестве реакционной координаты отдельных внутрициклических торсионных углов показано, что при расчете изолированной молекулы 1,3-диоксана I в вакууме наиболее оптимальный маршрут инверсии цикла этого соединения: К ↔ К*- проходит через переходное состояние (ПС), отвечающее форме софы, С₁ (табл.1).

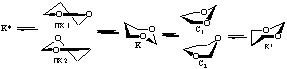
Таблица 1. Расчетные барьеры инверсии К↔К* (∆Е^≠) диоксана I, ккал/моль

Менее вероятны пути инверсии, идущие через ПС С₂, ПК1 и ПК2 (формы полукресла). Экспериментальная величина ∆G^≠ по данным [4] составляет 9.0-10.1 ккал/моль. Промежуточный минимум (ПМ) на ППЭ соответствует формам 1,4- либо 2,5-твист.

Исследование ППЭ соединения I с помощью полуэмпирических (АМ1 и РМ3) и неэмпирических (STO-3G и 6-31G) методов выявило более общую картину возможных конформационных превращений, а также характер промежуточных минимумов (ПМ) и переходных состояний (ПС) (табл.2).

Таблица 2. Энергетические параметры инверсии КÛК* (ккал/моль)

Полученные данные свидетельствуют о двух вероятных путях конформационной изомеризации К↔К*, из которых в рамках полуэмпирических методов несколько более предпочтителен маршрут, идущий через промежуточный минимум 1,4-Т, а в неэмпирическом приближении - через 2,5-Т. Отмеченные гибкие формы способны превращаться друг в друга через переходное состояние ПС-2. Основному максимуму на ППЭ (ПС-1) отвечает форма софы.

В случае соединений II и III исследованы только два основных минимума, отвечающих конформерам кресла с аксиально и экваториально ориентированными заместителями (Ка и Ке соответственно).

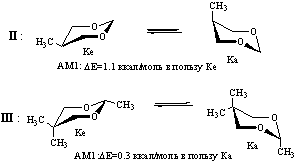
По данным литературы форма Ке более устойчива, чем Ка (величина ∆G⁰ С⁵-СН₃ составляет 0.8-0.9 ккал/моль, а ∆G⁰ С²-СН₃ - 3.6-4.1 ккал/моль [4]. Результаты расчетов показывают, что метод АМ1 достаточно корректно воспроизводит различия в энергии конформеров диоксана II, однако весьма неточен при оценке относительной стабильности форм Ка и Ке диоксана III, существенно завышая энергию экваториального конформера.

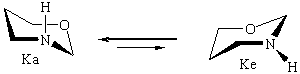
Исследование характера ППЭ молекул незамещенного тетрагидро-1,3-оксазина IV с помощью пакета HyperChem также выявило два вероятных маршрута конформационной изомеризации между невырожденными по энергии конформерами кресла Ка и Ке (форма Ка в согласии с данными ЯМР эксперимента более устойчива [5,6]). Полученные данные представлены в табл.3.

Таблица 3. Энергетические параметры инверсии Ка↔Ке (ккал/моль)

В этом случае на ППЭ присутствует три максимума; главному из них отвечает форма софы ПС-2. Кроме того, гибкие формы 1,4-Т и 2,5-Т способны превращаться друг в друга через переходное состояние ПС-3 [8].

2. Моделирование поверхности потенциальной энергии 1,3-диоксанов и тетрагидро-1,3-оксазина в присутствии гексапептидов

Известно, что существующие биорецепторы относятся к белкам; при этом молекула активного (в частности, лекарственного) субстрата связывается определенным участком белковой молекулы. Однако природа, структура и конкретный характер рецепторов, принимающих участие в связывании молекул 1,3-диоксанов и тетрагидро-1,3-оксазинов, неизвестны. Очевидно лишь, что биомолекула оказывает большое влияние на лекарственный субстрат, существенно перестраивая энергетику конформационных превращений последнего. В этой связи с целью моделирования взаимодействия в системе "рецептор - субстрат" на начальном этапе связывания, нами исследовано конформационное поведение молекул соединений I-IV в присутствии произвольных ациклического (П₁) и циклического (П₂) гексапептидов, построенных из остатков L-аминокислот, связанных по β-типу.

П₁: ALA-GLY-SER-ASN-LEU-ASP

Сконструированные с помощью программного обеспечения HyperChem молекулы отмеченных гексапептидов с цвиттер-ионными концевыми группами, были оптимизированы в рамках эмпирической программы c силовым полем Amber, а затем - с помощью полуэмпирического метода АМ1. Далее в различных положениях вблизи молекулы гексапептида размещались 1,3-диоксаны I-III либо оксазин IV, предварительно оптимизированные в рамках АМ1, и система "гетероцикл - пептид" оптимизировалась с помощью приближения АМ1. Полученные результаты представлены в табл.4-7 и на рис.1-3.

Е (АМ1), ккал/моль

Гексапептид:    -7476.45; ∑Е пепт. и Е цикл.

1,3-диоксан (кресло): -1321.55;∑= -8798.0

1,3-диоксан (1,4-Т):     -1319.21;∑= -8795.66

1,3-диоксан (НВ):        -1318.56; ∑=-8795.01

Таблица 4. Система: гексапептид П₁- 1,3-диоксан

Тетрагидро-1,3-оксазин (кресло, NH a): -1376.97; ∑=-8853.42;

Тетрагидро-1,3-оксазин (кресло, NH e): -1372.07;∑= -8848.52;

Тетрагидро-1,3-оксазин (1,4-твист, NHa): -1374.03;∑= -8850.48;

Таблица 5. Система: гексапептид П₁ - тетрагидро-1,3-оксазин

Нетрудно видеть, что для системы "П₁ - 1,3-диоксан" наблюдается ряд важных закономерностей:

1. Выигрыш в энергии ∆Е (по сравнению с суммой энергий изолированных молекул гексапептида и 1,3-диоксана) существенно зависит от взаимного расположения молекул и уменьшается в случае расположения диоксана со стороны цвиттер-ионных концевых групп.
2. Нивелируются различия в энергии между креслом и гибкой формой 1,4-Т (последняя обуславливает максимальное значение ∆Е, табл.4); в то же время конформер, отвечающий другому промежуточному минимуму - 2,5-Т - не реализуется вовсе, а в ходе оптимизации превращается в 1,4-Т.
3. За счет межмолекулярных водородных связей становится возможной стабилизация формы, соответствующей переходному состоянию между 1,4-Т и 2,5-Т конформерами (несимметричная ванна НВ, рис.2).

Несколько иные закономерности наблюдаются в системе "П₁ - тетрагидро-1,3-оксазин": уменьшение различий в энергии между аксиальным и экваториальным конформерами кресла и увеличение ∆Е между формами Ка и 1,4-Т (данные получены для соответственно одинаковых взаимных позиций оксазина и гексапептида (табл.5).

В вакууме: ∆E(NHa-NHe) = 4.9 ккал/моль

В прис. гексапептида: ∆E(NHa-NHe) = 3.4 ккал/моль

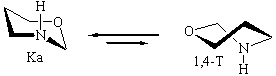
В вакууме: ∆E(К NHa-1,4-Т NHа) = 2.9 ккал/моль

В прис. гексапептида: ∆E(К NHa-1,4-Т NHа) = 3.9 ккал/моль

Общая картина взаимного расположения молекул насыщенного гетероцикла (на примере 1,3-диоксана) и гексапептида иллюстрируется рис.1:

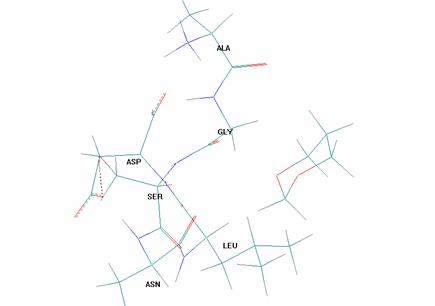
Рисунок 1. Общая картина взаимного расположения молекул насыщенного гетероцикла

На рис. 2 представлен пример стабилизации ПС - конформации НВ - за счет межмолекулярной водородной связи (показана пунктиром):

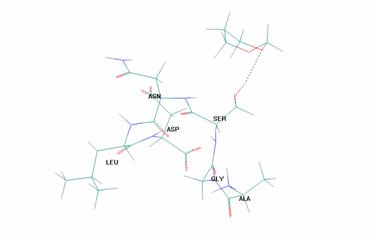
Рисунок 2. Пример стабилизации ПС - конформации НВ - за счет межмолекулярной водородной связи (показана пунктиром)

Для случая координации двух молекул 1,3-диоксана с пептидом П₁ выигрыш в энергии составляет 17.1 ккал/моль (рис.3):

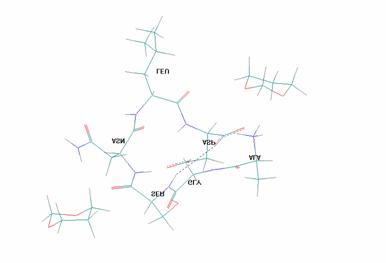
Рисунок 3. Координации двух молекул 1,3-диоксана с пептидом П₁ выигрыш в энергии

В случае системы "П₂ - 1,3-гетероцикл" с циклическим гексапептидом выигрыш в энергии для 1,3-диоксанов I-III сравним с наблюдаемым для системы с пептидом П₁; в то же время различие в энергии аксиальных и экваториальных конформеров соединений II и III (∆Е´) по сравнению с рассчитанным для изолированных молекул заметно возросло (табл.6).

Таблица 6. Система: гексапептид П₂ - 1,3-диоксаны I (№ 1-3), II (№ 4,5) и III (№ 6,7)

* В пользу Ке для диоксана II и Ка для диоксана III.

Для оксазина IV система с пептидом в ряде случае менее выгодна по сравнению с суммой энергий изолированных молекул (отрицательные значения ∆Е, табл.7).

Таблица 7. Система: гексапептид П₂ - 1,3-тетрагидрооксазин

Наименьшее расстояние между молекулой гетероцикла и ближайшим фрагментом гексапептида во всех случаях составляет 2.2-2.3 Å, что является типичным для длины межмолекулярной водородной связи в большинстве органических молекул.

Полученные данные свидетельствуют о существенном влиянии молекулы пептида на характер конформационной изомеризации исследованных 1,3-гетероциклов и показывают, что в процесс связывания модельных соединений с биомолекулой вовлечены не только стабильные конформеры, но и формы, соответствующие локальным максимумам на ППЭ.

СПИСОК ЛИТЕРАТУРЫ

1. Итоги науки и техники. Технология органических веществ. Т.5. Химия и технология 1,3-диоксациклоалканов /Д.Л. Рахманкулов, Р.А. Караханов, С.С. Злотский и др. //М.: ВИНИТИ, 1979. - 288 с.
2. Романов И.А., Талипова Г.Р., Ханченко М.В. и др. //Основной органический синтез и нефтехимия. Сб. научн. трудов. Вып. 26. Ярославль, 1990. - С.118-130.
3. HyperChem 5.02. Trial version. http://www.hyper.com/.
4. Внутреннее вращение молекул /под ред. В.Дж. Орвилл-Томаса. М.: Мир, 1975. - С.355.
5. Cook M.J., Jones R.A.Y., Katritzky A.R. et al. //J. Chem. Soc. Perkin Trans. - 1973. - N 4. - P.325-331.
6. Ferguson I.J., Katritzky A.R., Read D.M. //J. Chem. Soc. Chem. Comm. - 1975. - N 7. - P.255-256.
7. Файзуллин А.А. Материалы XXXVIII международной научной студенческой конференции "Студент и научно-технический прогресс". Химия. Новосибирск, 2000. - С.141.
8. Файзуллин А.А., Бочкор С.А., Кузнецов В.В. Четвертая Всероссийская научная internet-конференция "Компьютерное и математическое моделирование в естественных и технических науках". Тамбов, 2002. - Вып.18. - С.55.

Библиографическая ссылка