Введение
Управление теплогенерирующими установками (ТГУ), особенно на основе органического цикла Ренкина (ORC – Organic Rankine Cycle) [1, 2] с применением разных подходов [3], сталкивается с проблемой параметрической неопределенности, вызванной изменением тепловых нагрузок, колебаниями расхода теплоносителя, старением оборудования и неточностями в термодинамических свойствах рабочего тела. Традиционные системы управления с фиксированными параметрами, такие как ПИД-регуляторы, не обеспечивают устойчивую и эффективную работу в таких условиях. Следует отметить, что традиционные теплогенерирующие установки, такие как широко распространенные котлы типа Е(ДЕ), имеют специфические динамические характеристики, обусловленные их конструкцией и принципом работы [4], что также накладывает дополнительные требования к системам управления.
Однако, несмотря на значительный теоретический прогресс, практическое применение сложных адаптивных алгоритмов в теплоэнергетике часто сталкивается с проблемами, такими как вычислительная сложность, необходимость точной идентификации параметров в условиях сильных внешних возмущений и обеспечение робастной устойчивости замкнутой системы.
Цель исследования – разработка и апробация вычислительно эффективного способа адаптивного управления, сочетающего метод прогнозирующего управления на основе модели (MPC – Model Predictive Control) с упрощенными процедурами онлайн-идентификации, специально предназначенного для задач управления нестационарными процессами теплопередачи в теплогенерирующих установках. Научная новизна заключается в комбинации метод прогнозирующего управления на основе модели с алгоритмом рекуррентного метода наименьших квадратов (РМНК – Recursive Least Squares) для онлайн-коррекции параметров модели испарителя органического цикла Ренкина в условиях параметрического дрейфа.
Материалы и методы исследования
В качестве объекта исследования использована нестационарная математическая модель испарителя теплогенерирующей установки, функционирующей на основе органического цикла Ренкина (ORC) [5]. Модель построена в среде MATLAB/Simulink и основана на уравнениях баланса массы и энергии, описывающих одномерное течение рабочего тела и теплоносителя. В качестве рабочего тела принято условное органическое вещество со свойствами, близкими к R245fa.
Для имитации реальных условий эксплуатации в модель введены следующие источники параметрической неопределенности, характерные для промышленных ORC-установок:
‒ колебания температуры и расхода первичного теплоносителя (±25 % от номинального значения);
‒ постепенное снижение коэффициента теплопередачи на 20 % в течение эксперимента, моделирующее загрязнение поверхностей теплообмена [6].
Аппаратно-программная платформа исследования включает:
‒ программный комплекс MATLAB R2023b с пакетами Simulink, Control System Toolbox, System Identification Toolbox;
‒ персональный компьютер с процессором Intel Core i7 и ОЗУ 32 ГБ, обеспечивающий выполнение всех вычислений в режиме, приближенном к реальному времени.
1. Постановка задачи
Для обеспечения максимальной эффективности системы ORC необходимо управлять ключевыми термодинамическими параметрами. Основные задачи включают:
1. Поддержание стабильного и безопасного функционирования системы.
2. Оптимизацию выработки чистой электроэнергии.
3. Точное регулирование перегрева пара на входе в расширитель для предотвращения повреждения и максимизации эффективности.
4. Поддержание оптимального давления испарения для максимизации выходной мощности [7].
Надежная эксплуатация системы ORC является ключевым фактором для продления срока службы всех основных компонентов. В связи с этим точное регулирование перегрева испарителя на входе в расширительный механизм является приоритетной задачей для контроллера. Важно минимизировать перегрев для достижения максимальной термодинамической эффективности и предотвращения образования жидкостных капель на входе в расширитель, что может привести к повреждению расширительного механизма.
Динамика системы ORC может быть описана в общем виде нелинейной моделью «вход – состояние – выход»:
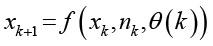 . (1)
. (1)
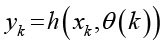 , (2)
, (2)
где xk – вектор состояния (энтальпия, давление) системы в момент времени k, xk+1 – вектор состояния на следующем временном шаге, f – нелинейная функция динамики, nk – вектор возмущений (шумов, внешних воздействий) в момент k, θ(k) – вектор параметров системы, зависящих от времени, yk – вектор измеряемых выходов (наблюдений) в момент k, h – нелинейная функция наблюдения.
Задача управления заключается в синтезе такого закона управления nk, который минимизирует отклонения выходных параметров от заданных значений и поддерживает оптимальный режим работы системы, несмотря на изменения параметров θ(k).
2. Предлагаемый метод адаптивного управления
В качестве решения предложен комбинированный алгоритм, состоящий из двух контуров: прогнозирующего контроллера (MPC) и контура онлайн-идентификации параметров.
Контур прогнозирующего управления
В основе лежит метод прогнозирующего управления на основе модели (MPC). На каждом шаге управления k решается задача оптимизации на горизонте прогнозирования N:
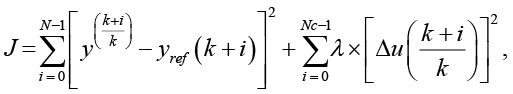 (3)
(3)
где J – целевая функция, k – текущий дискретный момент времени, N – количество шагов вперед, на которое модель предсказывает поведение схемы, 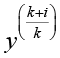 – прогнозируемое значение входа системы в момент k+i, сделанное в момент k, yref(k+i) – заданное (желанное) значение выхода в момент времени k+i. Nc – количество шагов, на которых оптимизируются управляющее воздействие,
– прогнозируемое значение входа системы в момент k+i, сделанное в момент k, yref(k+i) – заданное (желанное) значение выхода в момент времени k+i. Nc – количество шагов, на которых оптимизируются управляющее воздействие, 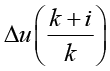 – изменение управляющего воздействия на шаге k+i, спрогнозированное в момент k, λ – весовой коэффициент, регулирующий компромисс между точностью отслеживания желаемой траектории и энергией/плавностью управления.
– изменение управляющего воздействия на шаге k+i, спрогнозированное в момент k, λ – весовой коэффициент, регулирующий компромисс между точностью отслеживания желаемой траектории и энергией/плавностью управления.
Оптимизация проводится при наличии ограничений на управляющие воздействия и состояния системы. Ключевая модификация по сравнению со стандартным MPC заключается в том, что для прогнозирования используется модель, параметры которой не фиксированы, а адаптивно настраиваются в контуре идентификации [8].
Контур онлайн-идентификации параметров. Для снижения вычислительной сложности применяется рекуррентный метод наименьших квадратов (РМНК) с экспоненциальным забыванием. Алгоритм РМНК позволяет в реальном времени уточнять оценки параметров θ(k) на основе последних измерений входов u(k) и выходов y(k) системы:
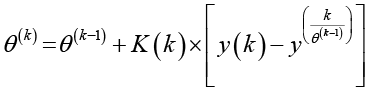 . (4)
. (4)
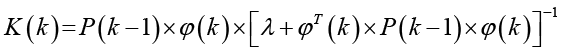 . (5)
. (5)
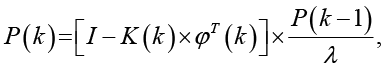 (6)
(6)
где θ(k) – текущая оценка вектора параметров,
K(k) – коэффициент усиления,
P(k) – ковариационная матрица,
φ(k) – вектор регрессии, содержащий прошлые значения входов и выходов,
λ = 0,95 – коэффициент забывания (0<λ≤1), позволяющий алгоритму адаптироваться к изменяющимся параметрам.
Упрощение, делающее метод применимым на практике, заключается в идентификации параметров линеаризованной модели «вход – выход» в окрестности текущей рабочей точки, что значительно снижает вычислительную нагрузку по сравнению с идентификацией параметров полной нелинейной модели.
Взаимодействие контуров. На каждом шаге:
Контур идентификации на основе последних данных уточняет θ(k).
Обновленная модель с параметрами θ(k) передается в MPC.
MPC решает задачу оптимизации и вычисляет оптимальное управляющее воздействие u(k).
Воздействие применяется к объекту, процесс повторяется.
3. Математическая модель объекта управления
Для исследования эффективности предложенного механизма рассмотрена нестационарная модель теплообмена в испарителе ORC. Установка, работающая на органическом цикле Ренкина [9], должна обеспечивать надежное производство электрической энергии, контролировать основные параметры, иметь запас рабочего тела на пуск и останов установки [10]. Модель основана на уравнениях энергии и массы, записанных в предположении одномерного течения. Параметрическая неопределенность вводится в виде изменяющихся во времени коэффициентов теплоотдачи и гидравлического сопротивления, что моделирует такие эффекты, как загрязнение поверхностей теплообмена и изменение свойств теплоносителя. Также возможно совмещение методики с различными средствами автоматизации, например концепцией BIM-проектирования, это позволит усилить ее достоинства. Это согласуется с общим трендом на внедрение цифровых технологий в тепловые расчеты и проектирование теплогенерирующих установок, что позволяет создавать более точные цифровые двойники и оптимизировать процессы на ранних этапах [11].
Следовательно, упрощение приведения к однослойной модели требует оценки дискретных физических свойств и моделируется с помощью асимметричных единичных функций Хевисайда. Известны применения этого метода для моделирования первой стадии неустойчивой теплопроводности. В частности, его применяют к процессу горения [12, 13].
Модель основана на уравнениях энергии и массы, записанных в предположении одномерного течения. Параметрическая неопределенность вводится в виде изменяющихся во времени коэффициентов теплоотдачи и гидравлического сопротивления, что моделирует такие эффекты, как загрязнение поверхностей теплообмена и изменение свойств теплоносителя.
Динамика системы описывается системой дифференциальных уравнений в форме Коши, которая затем дискретизуется для целей управления и идентификации. Именно параметры этой дискретной модели (коэффициенты передаточной функции) подлежат онлайн-идентификации с помощью РМНК.
Результаты исследования и их обсуждение
Количественные результаты моделирования представлены в таблице ниже. В качестве метрик использовались среднеквадратичное отклонение (RMSE – Root Mean Square Error) и максимальное отклонение по ключевым переменным: перегрев пара и давление испарения (табл. 1).
Анализ результатов:
1. ПИД-регулятор демонстрировал значительное перерегулирование и длительное время возврата к заданному режиму, а его производительность резко ухудшалась при изменении динамики системы (загрязнение).
2. Стандартный MPC показал лучшие результаты по подавлению возмущений в номинальном режиме, однако при параметрическом дрейфе (загрязнение) его производительность деградировала, возникали устойчивые отклонения, так как модель переставала соответствовать объекту.
Таблица 1
Сравнительный результат моделирования
|
Критерий / Метод управления |
Традиционный ПИД-регулятор |
Стандартный MPC |
Предлагаемый адаптивный MPC |
|
RMSE: Перегрев пара, [°C] |
4,5 |
2,1 |
0,9 |
|
Макс. отклонение: Перегрев пара, [%] |
18 % |
9 % |
4 % |
|
RMSE: Давление испарения, [кПа] |
35 |
18 |
7 |
|
Время переходного процесса (после скачка нагрузки), [с] |
> 150 |
~90 |
< 50 |
|
Средняя генерируемая мощность (относительно номинала) |
100 % |
101,5 % |
103 % |
Примечание: составлена авторами на основе полученных данных в ходе исследования.
Таблица 2
Сравнительный результат переходных процессов
|
Время (с) |
Заданное/ необходимое значение (°С) |
Пропорционально- интегрально- дифференцированное управление (°С) |
Модельно- прогнозирующее управление (°С) |
Адаптивное управление (°С) |
|
0 |
25 |
25 |
25 |
25 |
|
1 |
25 |
25 |
25 |
25 |
|
2 |
25 |
25 |
25 |
25 |
|
3 |
25 |
25 |
25 |
25 |
|
4 |
25 |
35 |
28 |
26 |
|
5 |
25 |
32 |
26 |
25,5 |
|
6 |
25 |
28 |
25,5 |
25,2 |
|
7 |
25 |
26 |
25,2 |
25,1 |
|
8 |
25 |
25,5 |
25,1 |
25 |
|
9 |
25 |
25,2 |
25 |
25 |
|
10 |
25 |
25 |
25 |
25 |
|
11 |
25 |
22 |
23 |
24 |
|
12 |
25 |
23 |
24 |
24,5 |
|
13 |
25 |
24 |
24,5 |
24,8 |
|
14 |
25 |
24,5 |
24,8 |
24,9 |
|
15 |
25 |
24,8 |
24,9 |
25 |
Примечание: составлена авторами на основе полученных данных в ходе исследования.
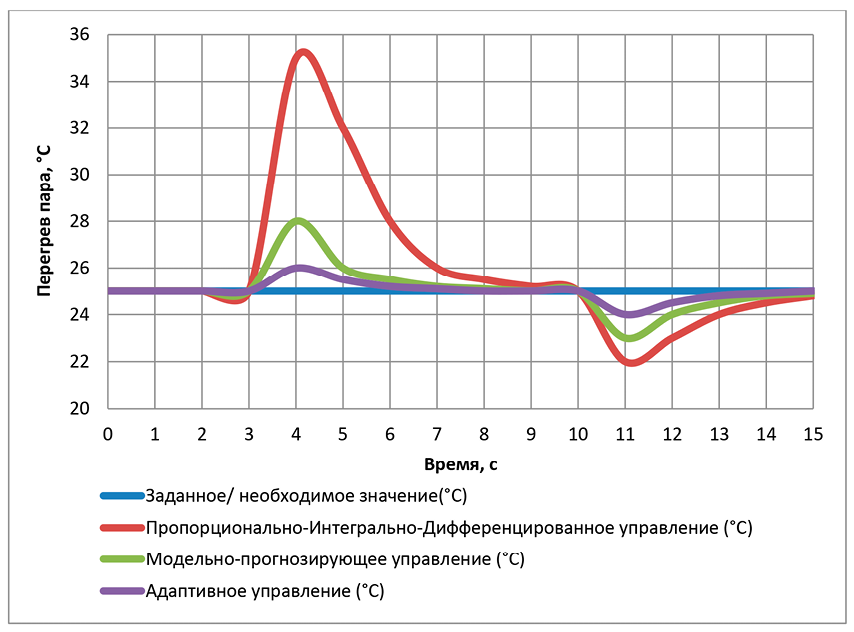
Рис. 1. Сравнение переходных процессов Примечание: составлен авторами по результатам данного исследования
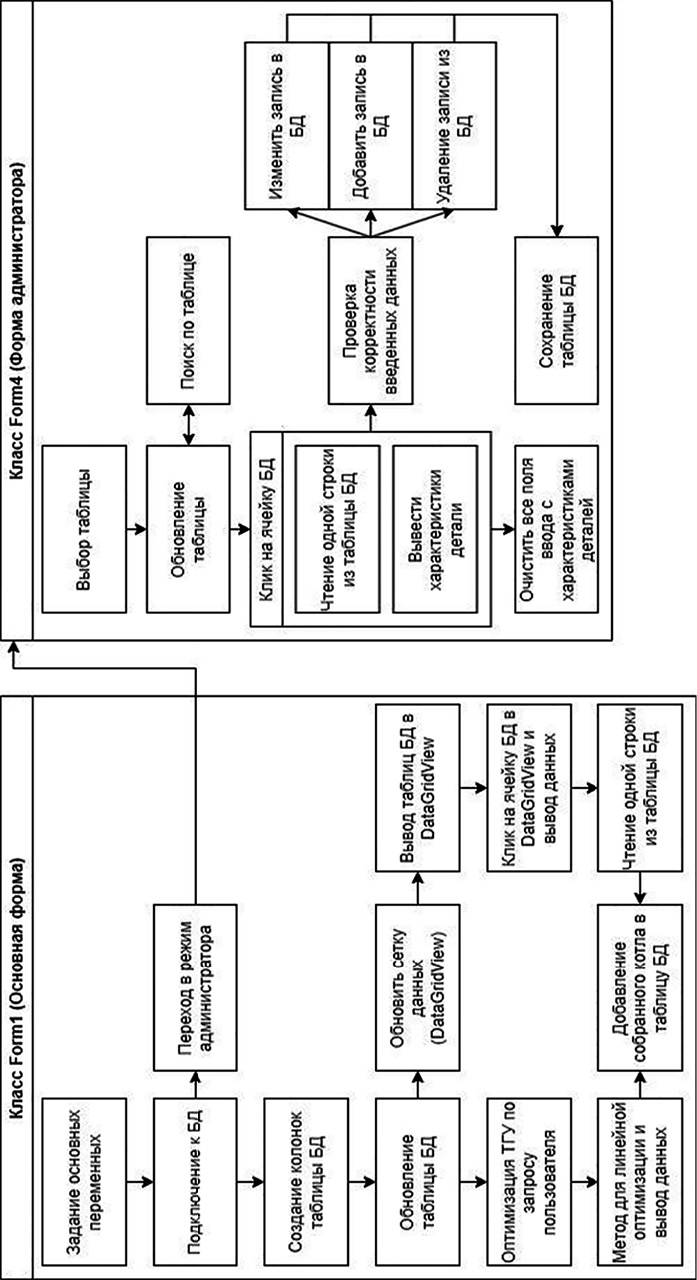
Рис. 2. Архитектура и механизм работы системы адаптивного проектирования ТГУ Примечание: составлена авторами по результатам данного исследования
3. Адаптивный MPC обеспечил наилучшее качество управления. Алгоритм успешно компенсировал изменения параметров модели в реальном времени, поддерживая близкий к оптимальному режим работы. Максимальные отклонения параметров были минимальными, а время переходного процесса – самым коротким. Более точное поддержание оптимального давления испарения позволило увеличить среднюю генерируемую мощность установки.
На основании результатов исследования составлена таблица со сравнительными результатами переходных процессов (табл. 2).
Исходя из табличных данных, построена диаграмма, иллюстрирующая сравнение переходных процессов (рис. 1).
Результаты моделирования подтвердили, что предложенный адаптивный механизм эффективно решает проблему параметрической неопределенности. Упрощенная процедура идентификации на основе РМНК не привела к значительным вычислительным затратам, что делает алгоритм применимым в системах реального времени.
Для практической реализации алгоритма была разработана концептуальная архитектура программного комплекса, предназначенного для сквозного проектирования ТГУ (рис. 2).
Эффективность подобных комбинированных подходов, интегрирующих прогнозирующее и адаптивное управление для сложных энергетических систем, также подтверждается исследованиями в смежных областях, например в управлении интегрированными энергосистемами зданий [14]. Использование современных методов, таких как компьютерное моделирование, алгоритмы оптимизации и системный анализ, позволяет снизить влияние человеческого фактора, минимизировать ошибки на этапе проектирования и улучшить адаптивность к изменяющимся условиям эксплуатации [15].
Заключение
В работе предложен вычислительно эффективный способ адаптивного управления для теплогенерирующих установок, основанный на интеграции прогнозирующего управления на основе модели (MPC) и онлайн-идентификации параметров с использованием рекуррентного метода наименьших квадратов. Проведенное имитационное моделирование показало, что разработанный подход обеспечивает существенное повышение точности регулирования ключевых параметров – перегрева пара и давления испарения – по сравнению с традиционным ПИД-регулированием и стандартным MPC.
Адаптивный алгоритм демонстрирует устойчивость к параметрическим возмущениям, таким как изменение тепловой нагрузки и снижение эффективности теплообмена, сокращая время переходного процесса более чем в 3 раза и повышая среднюю генерируемую мощность установки на 2–3 %.
Полученные результаты подтверждают, что предложенный механизм позволяет обеспечить надежную и энергоэффективную работу теплогенерирующих установок в условиях динамически меняющихся параметров, что делает его перспективным для практического внедрения в системы автоматизированного управления технологическими процессами (АСУ ТП). В дальнейшем планируется тестирование алгоритма на физических стендах и его интеграция в промышленные АСУ ТП.
В работе была исследована проблема параметрической неопределенности в системах управления ТГУ и предложен способ адаптивного управления для ее решения. Разработан и апробирован комбинированный механизм, интегрирующий MPC с упрощенными процедурами онлайн-идентификации на основе РМНК.
Проведенное имитационное моделирование показало, что предложенный механизм способен в реальном времени адаптироваться к изменяющейся динамике нестационарных процессов теплопередачи, поддерживая близкий к оптимальному режим работы системы.
Таким образом, реализация предложенного механизма позволяет существенно повысить энергетическую эффективность, надежность и робастность теплогенерирующих установок. Дальнейшие исследования планируется сосредоточить на тестировании механизма в условиях еще более широкого диапазона возмущений, а также на разработке специализированного программного обеспечения для встраивания данного механизма в автоматизированные системы управления технологическими процессами реальных промышленных объектов.
Конфликт интересов
Библиографическая ссылка
Коломыченко А.А., Коськин А.В. РЕАЛИЗАЦИЯ СПОСОБА АДАПТИВНОГО УПРАВЛЕНИЯ ПРОЦЕССОМ ПРОЕКТИРОВАНИЯ ТЕПЛОГЕНЕРИРУЮЩИХ УСТАНОВОК НА ОСНОВЕ ОРГАНИЧЕСКОГО ЦИКЛА РЕНКИНА // Современные наукоемкие технологии. 2026. № 1. С. 51-58;URL: https://top-technologies.ru/ru/article/view?id=40648 (дата обращения: 13.02.2026).
DOI: https://doi.org/10.17513/snt.40648



