Введение
Бурное развитие и внедрение технологии Wi-Fi Sensing, превращающей стандартную инфраструктуру беспроводных сетей IEEE 802.11 в инструмент пассивного мониторинга окружающего пространства, открывает беспрецедентные возможности в сферах умных помещений, телемедицины, промышленной автоматизации и систем безопасности. Фундаментальная возможность пассивного мониторинга окружающего пространства через анализ искажений радиосигнала – параметров его мощности (RSSI), состояния канала (CSI) и времени пролета (ToF/TDoA) – одновременно является источником уязвимостей этой технологии. Пассивный характер сбора высокодетализированных поведенческих данных, отсутствие явных индикаторов наблюдения и физическая природа атак формируют уникальные уязвимости, систематизированные в рамках предшествующих патентных и аналитических исследований. Как показывают работы [1, 2], данные CSI позволяют дистанционно восстанавливать широкий спектр действий. Включая ввод текста и паролей, что создает прямую угрозу конфиденциальности [3–5]. При этом патенты [6, 7] прямо указывают на уязвимость систем к атакам типа adversarial, приводящим к созданию «фантомных» объектов. Дальнейшие исследования углубляют анализ, рассматривая уязвимости систем, основанных на времени пролета сигнала (ToF) [8, 9]. Отдельно рассматриваются угрозы доступности, реализуемые через атаки на уровне RSSI [10–12]. Современная практика инженерии безопасности зачастую опирается на качественные или полуколичественные методологии управления рисками, такие как модель ФСТЕК, OCTAVE или NIST Cybersecurity Framework (CSF) [13]. Эти подходы, будучи ценными для формирования общей стратегии, демонстрируют существенные ограничения применительно к сложным, технологически специфичным системам, подобным Wi-Fi Sensing. Они плохо масштабируются для анализа десятков взаимосвязанных угроз и контрмер, не обеспечивают количественного обоснования выбора конкретных средств защиты и, что наиболее важно, практически не учитывают эффекты синергии и антагонизма между различными контрмерами при их совместном применении. В то же время продвинутые математические методы, включая многокритериальный анализ (MCDM) [14] и целочисленное линейное программирование (ILP) [15], хотя и предлагают формальный оптимизационный аппарат, обычно применяются в отрыве от глубокой специфики предметной области. Как следствие, они не позволяют корректно учесть такие особенности Wi-Fi Sensing, как различная критичность угроз для разных физических параметров сигнала (CSI, RSSI, ToF) или комплексное воздействие гибридных атак.
Особую актуальность приобретает задача учета синергетических эффектов. Современные исследования, включая систематические обзоры [16], указывают на доминирование в литературе анализа антагонизмов между мерами безопасности, в то время как потенциальные синергии, способные привести к сверхаддитивному повышению уровня защиты при рациональной комбинации контрмер, изучены недостаточно. Игнорирование этого фактора на практике может приводить к двум негативным сценариям: перерасходу бюджета на внедрение избыточных или конфликтующих мер и, наоборот, к недооценке эффективности правильно скомбинированного, но на первый взгляд скромного набора решений. Таким образом, формируется четко выраженный научно-практический пробел: между детальным качественным описанием уникальных угроз Wi-Fi Sensing и существующими общими методами оптимизации отсутствует связующее звено – специализированный количественный аппарат.
Цель исследования – разработка математического аппарата и алгоритмического инструментария для выбора и оптимизации контрмер, обеспечивающих максимальную безопасность систем мониторинга и распознавания объектов на основе беспроводных сетей стандарта IEEE 802.11 при заданных бюджетных ограничениях и требованиях к производительности.
Материалы и методы исследования
В работе применялся комплекс теоретико-прикладных методов, включающий математическое моделирование для формализации угроз и контрмер, количественную оценку рисков на основе интегральных показателей, методы оптимизации с бюджетными и эксплуатационными ограничениями, а также алгоритмический подход, реализующий жадную стратегию выбора контрмер. Для анализа компромиссов использованы методы визуализации данных, в частности построение трехмерной поверхности решений. Исследование опирается на разработанный математический аппарат (система расчетных формул, матрица эффективности), структурированные экспертные оценки угроз Wi-Fi Sensing, а также специализированное программное обеспечение, реализующее предложенные модели и алгоритмы.
Результаты исследования и их обсуждение
Модель оценки угроз
Пусть у нас есть множество угроз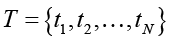 
и множество контрмер 
.
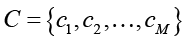Для каждой угрозы ti оценивается ее критичность по трем критериям: нарушение конфиденциальности (У₁); нарушение целостности (У₂); нарушение доступности (У₃).
Цель: найти подмножество контрмер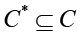 
, максимизирующее общий уровень безопасности при ограничениях на бюджет и производительность.
Для каждой угрозы ti ∈ T необходимо определить: потенциальный ущерб Уi, вероятность реализации Bi и радиус воздействия Pi.
Потенциальный ущерб оценивается по трем аспектам: конфиденциальность, целостность и доступность.
Уi =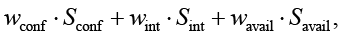
где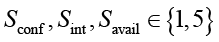 
– оценки нарушения конфиденциальности, целостности и доступности соответственно; 
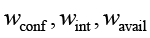– весовые коэффициенты, причем 
.
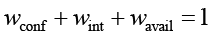Вероятность реализации угрозы определяется как
Bi = (Tc + Oc + Дс ) / 3,
где Tc ∈ {1,5} – техническая сложность реализации атаки; Oc ∈ {1,5} – доступность необходимого оборудования; Дc ∈{1,5} – требуемый уровень знаний атакующего.
Интегральный показатель угрозы (риск) при этом будет
Рискi = Уi ∙ Bi ∙ Pi ,
где Pi ∈ {0,1} – доля системы, подверженная угрозе.
Далее разрабатывается модель оценки контрмер.
Для каждой контрмеры cj ∈ C необходимо определить: вектор эффективности Эj ; вектор стоимости Сj ; вектор совместимости Кj ; сложность интеграции Пj.
Вектор эффективности:
Эj =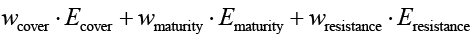 
,
где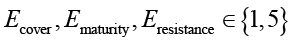 
– оценки покрытия угроз, технологической зрелости и сложности обхода соответственно; 
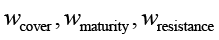– весовые коэффициенты, в сумме равные 1.
Вектор стоимости:
,
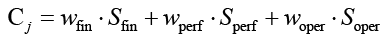где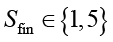 
– финансовые затраты (1 – высокие, 5 – низкие); 
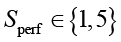– влияние на производительность (1 – сильное, 5 – отсутствует); 
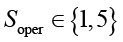– сложность эксплуатации (1 – сложная, 5 – простая); весовые коэффициенты 
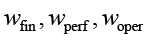в сумме равны 1. Обратная шкала применяется для того, чтобы более низкая стоимость напрямую увеличивала итоговую ценность контрмеры. Количественная оценка того, насколько легко и эффективно контрмера может быть интегрирована в существующую инфраструктуру Wi-Fi Sensing без необходимости кардинальной перестройки системы, выражается вектором совместимости:
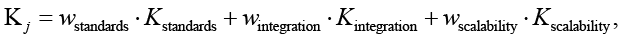
где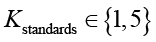 
– оценка соответствия контрмеры отраслевым стандартам и протоколам; 
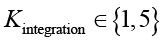– оценка сложности интеграции контрмеры в существующую инфраструктуру; 
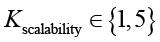– оценка способности контрмеры масштабироваться в системах разного размера; 
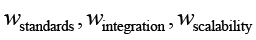– весовые коэффициенты, причем 
.
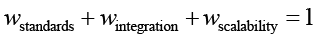Соответствие контрмеры отраслевым стандартам и протоколам оценивает, насколько контрмера соответствует общепринятым стандартам (например, IEEE 802.11bf, WPA3). Оценка близкая к 5 означает, что контрмера использует стандартные протоколы и легко встраивается в стандартную инфраструктуру. Оценка близкая к 1 указывает на использование уникальных решений, которые могут вызвать проблемы совместимости.
Сложность интеграции отражает трудоемкость внедрения контрмеры. Оценка 5 означает, что контрмера легко внедряется (например, путем обновления программного обеспечения), а оценка 1 – что требуется значительная перестройка инфраструктуры или замена оборудования.
Масштабируемость показывает, насколько хорошо контрмера работает в системах разного масштаба. Оценка 5 означает, что контрмера эффективно масштабируется без потери эффективности, 1, что она применима только в ограниченных условиях.
Весовые коэффициенты определяют важность каждого аспекта для конкретной системы. Матрица эффективности при этом будет иметь вид
,
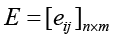где eij – эффективность контрмеры cj против угрозы ti вычисляется следующим образом:
eij = α∙Эj + β∙СпецЭij.
Специализированная эффективность (СпецЭij ∈ {0,1}) – это точечная мера того, насколько конкретная контрмера cⱼ целенаправленно защищает от конкретной угрозы tᵢ. СпецЭᵢⱼ = 1 – контрмера cⱼ идеально и целенаправленно блокирует угрозу tᵢ. Например, аппаратное шифрование CSI-данных (cⱼ) против перехвата CSI-паттернов (tᵢ). СпецЭᵢⱼ = 0 – контрмера не оказывает никакого специфического воздействия на данную угрозу. Например, система фильтрации сетевых пакетов (cⱼ) против атак на алгоритмы машинного обучения (tᵢ). 0 < СпецЭᵢⱼ < 1 – частичная эффективность, когда контрмера косвенно или ограниченно влияет на угрозу. Таким образом, параметр специализированной эффективности дает возможность учесть ситуацию, когда контрмера, демонстрируя среднюю общую эффективность, может быть максимально результативной против конкретной угрозы.
Весовые коэффициенты α и β определяют баланс между: универсальностью контрмеры (α), ее общей эффективностью Эⱼ против широкого спектра угроз и β – специализацией контрмеры (ее точечным воздействием СпецЭᵢⱼ на конкретную угрозу). При этом α + β = 1.
Типичные сценарии балансировки: α = 0.7, β = 0.3, приоритет универсальным решениям (например, при ограниченном бюджете); α = 0.3, β = 0.7, приоритет специализированной защите (например, для критических угроз); α = 0.5, β = 0.5, сбалансированный подход.
Функция целевой эффективности
Показатель ценности для пары угроза – контрмера отражает, насколько эффективно контрмера нейтрализует конкретную угрозу с учетом степени ее совместимости и совокупных затрат на внедрение, позволяя сравнивать различные средства защиты между собой и выбирать решения с максимальной отдачей на единицу вложенных ресурсов:
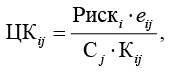
где Kij ∈ {0,1} – коэффициент совместимости контрмеры cj с существующей инфраструктурой при противодействии угрозе ti .
Общий показатель ценности контрмеры при этом
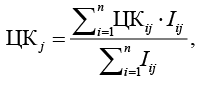
где Iij – индикатор применимости контрмеры cj к угрозе ti :
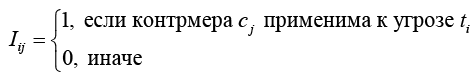
Для учета взаимодействия контрмер при их совместном применении вводится матрица синергии:
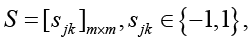
где sjk – коэффициент синергии между контрмерами cj и ck.
Общая формула коэффициента синергии:
,
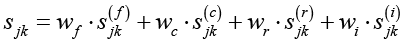где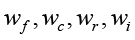 
– весовые коэффициенты компонентов синергии; 
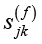– компонент функциональной синергии; 
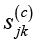– компонент синергии покрытия; 
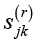– компонент ресурсной синергии; 
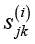– компонент информационной синергии. При этом условие нормировки весовых коэффициентов: 
.
Функциональная синергия отражает взаимное усиление функциональных возможностей контрмер:
,
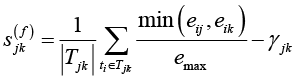где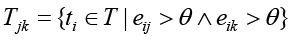 
– множество угроз, против которых эффективны обе контрмеры; eij, eik – эффективности контрмер cj и ck против угрозы ti; emax = 5 – максимальное значение эффективности; 
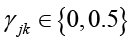– корректирующий коэффициент за функциональные конфликты между контрмерами; θ = 0,3 – порог значимой эффективности.
Синергия покрытия:
,
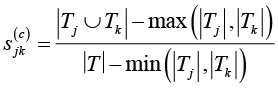где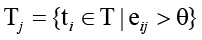 
– множество угроз, эффективно покрываемых контрмерой cj;
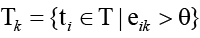– множество угроз, эффективно покрываемых контрмерой ck;
|T|=n – общее количество угроз;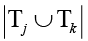 
– мощность объединения множеств.
Ресурсная синергия:
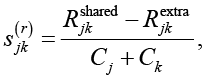
где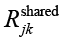 
– экономия ресурсов за счет совместного использования инфраструктуры; 
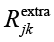– дополнительные затраты на интеграцию контрмер; Cj и Ck – стоимости внедрения контрмер cj и ck.
Информационная синергия:
,
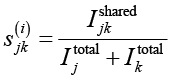где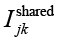 
– объем полезной информации, которую контрмера cj может предоставить ck; 
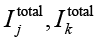– общий объем информации, обрабатываемой контрмерами.
Синергетическая эффективность контрмеры:
,
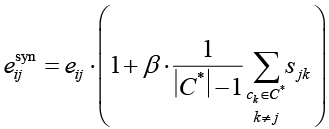где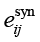 
– эффективность контрмеры cj против угрозы ti с учетом синергии; eij – базовая эффективность контрмеры; β ∈ {0,0,3} – коэффициент влияния синергии на эффективность; C* – выбранное подмножество контрмер; |C*| – количество контрмер в выбранном подмножестве.
После количественной оценки угроз и анализа эффективности контрмер необходимо определить такое подмножество контрмер, которое обеспечивает максимальное снижение совокупного риска при соблюдении бюджетных ограничений, требований к производительности системы и гарантированном покрытии критических угроз. Формализация этой задачи в виде целевой функции с системой ограничений и разработка эффективного алгоритма решения позволят произвести рациональное распределение ресурсов безопасности.
Формулировка задачи оптимизации
Максимизировать целевую функцию для выбираемого подмножества контрмер:
,
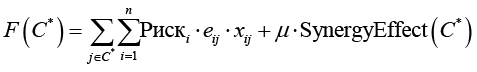где Рискi – интегральный риск i-й угрозы; eij – эффективность контрмеры cj против угрозы ti; xij ∈ {0,1} – индикатор применения контрмеры cj к угрозе ti; μ ≥ 0 – коэффициент значимости синергии.
При бюджетном ограничении:
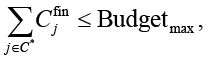
где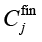 
– финансовый компонент стоимости контрмеры cj.; Bmax – максимально допустимый бюджет
Ограничение на производительность:
,
где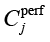 
– компонент производительности контрмеры cj; Perfmin – минимально допустимый уровень производительности системы.
Ограничение на покрытие критических угроз:
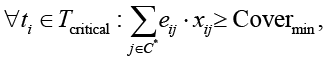
где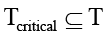 
– множество критических угроз; Covermin – минимальный требуемый уровень снижения риска для критических угроз; xij ∈ {0,1} – индикатор применения контрмеры cj к угрозе ti.
Ограничение на совместимость контрмер (синергия):
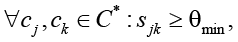
где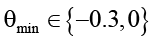 
– минимально допустимый уровень синергии.
Ограничение на обязательные контрмеры:
,
где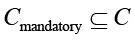 
– множество обязательных контрмер (например, по требованиям регуляторов).
Логические ограничения:
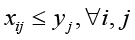
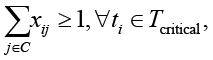
где yj ∈ {0,1} – бинарная переменная выбора контрмеры cj в набор C*; xij ∈ {0,1} – бинарная переменная применения контрмеры cj к угрозе ti.
Ограничение на максимальное количество контрмер:
,
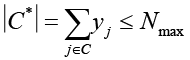где Nmax – максимальное количество контрмер (ограничение сложности системы).
Синергетический эффект:
,
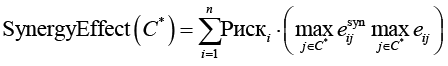где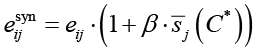 
– эффективность с учетом синергии; 
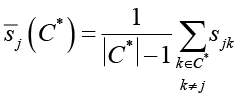– средняя синергия контрмеры cj с другими выбранными контрмерами; 
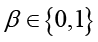– коэффициент влияния синергии на эффективность.
Остаточный риск после внедрения контрмер:
.
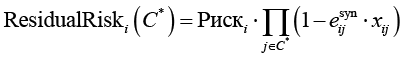Алгоритм оптимизации набора контрмер с учетом ограничений на бюджет, производительность и покрытие критических угроз представлен на рис. 1.
На первом шаге для каждой контрмеры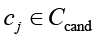 
производится расчет модифицированного прироста целевой функции на единицу затрат:
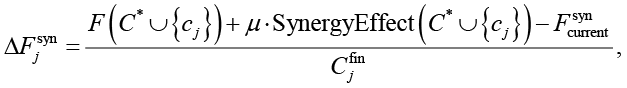
где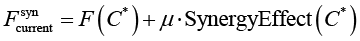 
– текущее значение целевой функции с учетом синергии, SynergyEffect(C*) вычисляется в соответствии с представленной моделью.
На втором шаге осуществляется выбор контрмеры с максимальным приростом. Из множества кандидатов выбирается контрмера:
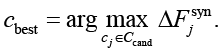
Если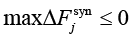 
, алгоритм переходит к Шагу 5 (Завершение).
На третьем шаге происходит проверка ограничений для контрмеры cbest. Перед добавлением контрмеры в оптимальный набор выполняется комплексная проверка выполнения бюджетного ограничения, ограничений производительности, покрытия критических угроз и совместимости (синергии) для временного множества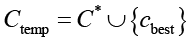 
. Если все ограничения выполняются, алгоритм переходит к Шагу 4. В противном случае контрмера cbest исключается из множества кандидатов (
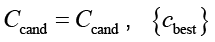) и осуществляется возврат к Шагу 2 для выбора следующего наилучшего кандидата.
На четвертом шаге контрмера cbest добавляется в оптимальный набор, а все связанные переменные и множества обновляются:
C* = C*⋃{cbest}, Costcurrent = Costcurrent+Cbestfin,
Perfcurrent = Perfcurrent ∙ Pbest, Fcurrentsyn = F(C*) + μ ∙ SynergyEffect(C*).
Из Ccand исключается выбранная контрмера, а также все контрмеры, имеющие с ней недопустимый антагонизм:
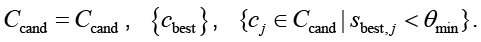
После обновления данных осуществляется возврат к Шагу 1 для следующей итерации основного цикла.
На пятом шаге алгоритм завершает работу, когда множество кандидатов пусто (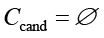
) или не осталось контрмер, дающих положительный прирост эффективности (
). На выходе алгоритма возвращается найденное оптимальное (субоптимальное) множество контрмер C* и рассчитываются итоговые показатели: общая стоимость внедрения, остаточный риск, интегральный коэффициент синергии, эффективность использования бюджета.
Общая стоимость внедрения:
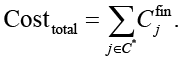
Остаточный риск с учетом синергетического повышения эффективности контрмер:
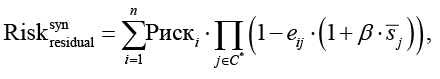
где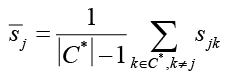
– средняя синергия контрмеры cj с другими выбранными средствами защиты.
Интегральный коэффициент синергии для выбранного набора:
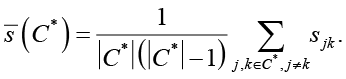
Эффективность использования бюджета:
Рис. 1. Алгоритм оптимизации набора контрмер с учетом ограничений на бюджет, производительность и покрытие критических угроз Примечание: составлен авторами по результатам данного исследования
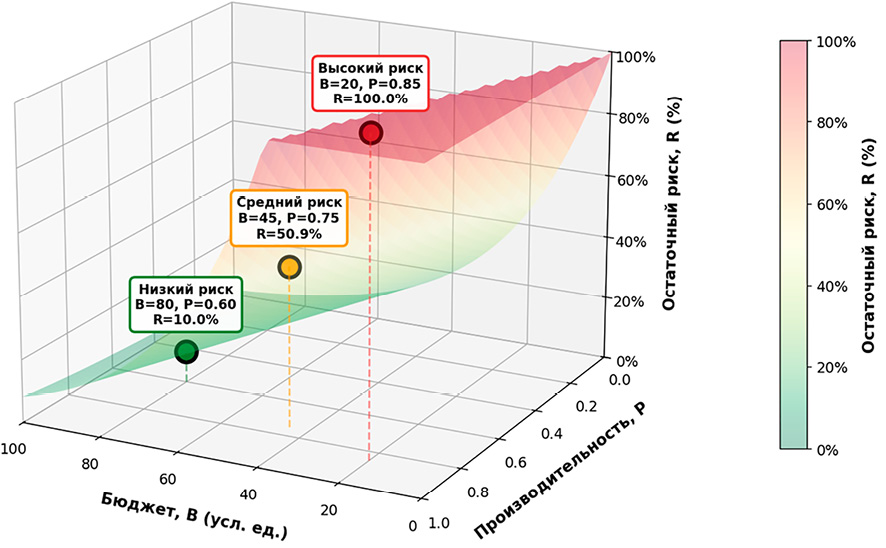
Рис. 2. Трехмерная модель зависимости остаточного риска от бюджета и требований к производительности Примечание: составлен авторами по результатам данного исследования
Для получения более сбалансированного решения опционально можно произвести постоптимизационную корректировку, в ходе которой из набора C* последовательно удаляются наименее эффективные с точки зрения отношения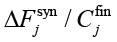 
контрмеры до тех пор, пока не будут выполнены все ограничения. Это позволяет освободить бюджет для потенциально более выгодных комбинаций контрмер на последующих итерациях модифицированного алгоритма.
Разработанный математический аппарат позволяет не только рассчитывать оптимальный набор средств защиты, но и наглядно анализировать фундаментальный компромисс между тремя ключевыми параметрами системы: бюджетом, минимальной производительностью и остаточным риском. Для визуальной наглядности была построена трехмерная модель зависимости остаточного риска от бюджета и требований к производительности (рис. 2).
Представленная трехмерная модель отражает общие закономерности поведения системы, однако для получения точных, пригодных для реализации результатов необходимо применять разработанный оптимизационный алгоритм. Это связано с тем, что алгоритм учитывает дискретную природу выбора контрмер, что может приводить к ступенчатому характеру зависимостей. Таким образом, визуализация служит эффективным инструментом для выявления трендов и поддержки стратегических решений на этапе предпроектного анализа, в то время как алгоритм обеспечивает точное количественное обоснование для итогового проектирования.
Заключение
В ходе исследования разработан комплексный математический аппарат для оптимизации выбора средств защиты в системах Wi-Fi Sensing. Аппарат включает формальные модели угроз и контрмер, метод расчета интегрального риска, механизм оценки эффективности контрмер, целевую функцию с системой ограничений, а также алгоритм последовательного выбора оптимального набора защитных мер. Данный инструментарий позволяет перейти от качественного описания уязвимостей к количественному обоснованию решений по кибербезопасности и предоставляет архитекторам систем формальную основу для принятия взвешенных решений. Однако эффективное применение этого аппарата требует понимания фундаментального компромисса, лежащего в основе любого проектирования системы безопасности.
Этот компромисс заключается в треугольнике взаимоисключающих требований: стремление обеспечить высокую производительность системы при минимальном финансировании мер безопасности закономерно ведет к существенному остаточному риску. Подобный подход может быть допустим лишь для систем, работающих с некритичными данными, где последствия реализации угроз являются приемлемыми. Для ответственных применений Wi-Fi Sensing оптимальная стратегия защиты должна формироваться не интуитивно, а на основе комплексного анализа всей поверхности решений, рассматривающей взаимосвязь бюджета, производительности и уровня риска, а не фокусироваться на отдельных изолированных сценариях. Разработанный математический аппарат, таким образом, служит основой для построения и анализа такой многомерной поверхности компромиссов, позволяя найти рациональный баланс между противоречивыми целями проектирования.
Практическая значимость работы заключается в предоставлении специалистам методической основы для обоснованного выбора контрмер, позволяющей избежать как недостаточного, так и избыточного инвестирования в безопасность.
Конфликт интересов
Библиографическая ссылка
Сарайкин А.И., Парфёнов Д.И. МАТЕМАТИЧЕСКИЙ АППАРАТ И АЛГОРИТМ ОПТИМИЗАЦИОННОГО ВЫБОРА КОНТРМЕР ПРОТИВ УГРОЗ БЕЗОПАСНОСТИ В СИСТЕМАХ WI-FI SENSING // Современные наукоемкие технологии. 2025. № 12. С. 174-183;URL: https://top-technologies.ru/ru/article/view?id=40619 (дата обращения: 21.01.2026).
DOI: https://doi.org/10.17513/snt.40619