Введение
Исследование конвективного теплообмена в каналах, заполненных пористыми средами, имеет фундаментальное и прикладное значение для множества передовых технологий, таких как системы аварийного охлаждения активных зон ядерных реакторов, высокоэффективные компактные теплообменники, каталитические реакторы, системы рекуперации тепла и терморегулирования электронной аппаратуры [1]. Особый интерес для создания таких устройств представляют современные структурированные пористые материалы на основе трижды периодических минимальных поверхностей (ТПМП), обладающие оптимальным сочетанием прочности, проницаемости и развитой площади поверхности теплообмена [2]. Классическая задача Гретца о развитии температурного поля в канале при заданной температуре стенки служит краеугольным камнем в теории конвективного теплообмена и многократно обобщалась для учета специфики течений в насыщенных пористых средах [3, 4].
В ранних исследованиях, опиравшихся на модель однотемпературной среды, обычно предполагалось состояние локального термического равновесия (ЛТР), при котором температуры твердого каркаса и жидкости в каждой точке пространства совпадают [5]. Однако в реальных условиях, например при высоких скоростях течения, низкой теплопроводности каркаса или малом коэффициенте межфазного теплообмена, это допущение часто не выполняется. В таких режимах возникает существенная разность температур между фазами, что требует перехода к двухтемпературным моделям или моделям локального термического неравновесия (ЛТН) [6]. Игнорирование этого эффекта может привести к значительным погрешностям в расчете тепловых потоков.
Важным физическим эффектом, сопровождающим фильтрацию жидкости в пористой матрице, является также вязкая диссипация механической энергии, превращающая работу сил трения в тепло. Ее вклад становится определяющим в высокоскоростных течениях, в высоковязких жидкостях или в средах с малой проницаемостью. Влияние диссипации на теплообмен в условиях локального неравновесия изучено недостаточно полно, особенно для трехмерных течений в каналах некруглого сечения, где геометрия поперечного сечения существенно усложняет картину теплопереноса [7].
Аналитические решения подобных сопряженных задач представляют особую ценность, так как позволяют не только получить точные зависимости для ключевых параметров, но и выявить фундаментальные физические закономерности, служа надежным эталоном для верификации и тестирования численных методов [8, 9]. Теоретические основы теплопроводности, заложенные в классических и обобщенных моделях [10, 11], остаются актуальным инструментом для таких исследований. При моделировании сложных пористых структур, подобных поверхности Фишера – Коха S, особое значение приобретают современные методы численного анализа, разработанные в работах [12–14]. Подробное исследование топологии и свойств ТПМП представлено в [15].
Несмотря на значительное количество работ по каждому из указанных аспектов в отдельности, в литературе отсутствует комплексное трехмерное аналитическое решение, которое одновременно и строго учитывало бы как локально-неравновесные условия теплопереноса между фазами, так и вклад вязкой диссипации энергии, с последующим детальным анализом динамики локального числа Нуссельта. Восполнение этого пробела позволит более адекватно описывать теплообмен в широком классе практических устройств с пористыми вставками.
Цель исследования – получение полного аналитического решения трехмерной задачи Гретца для пористого прямоугольного канала в локально-неравновесных условиях с учетом диссипации и анализ влияния определяющих безразмерных критериев на тепловые характеристики.
Материал и методы исследования
Рассматривается стационарная вынужденная конвекция в пористом прямоугольном канале с поперечными размерами −H ≤ y ≤ H, −H ≤ z ≤ H и продольной координатой 0 ≤ x < ∞ (рис. 1). Параметр H представляет собой половину ширины и половину высоты канала (м). Среда состоит из твердого каркаса и жидкой фазы, заполняющей поровое пространство. Физическая модель предполагает, что пористая среда является однородной, изотропной, жесткой и неподвижной, а течение – ламинарным и гидродинамически стабилизированным.
Принята ключевая гипотеза локально-неравновесных условий теплообмена, поэтому температуры жидкой Tf и твердой Ts фаз различны и описываются независимыми уравнениями энергии. Стенки канала поддерживаются при постоянной температуре Tw, на входе (x = 0) температура жидкости постоянна и равна Tin ≠ Tw.
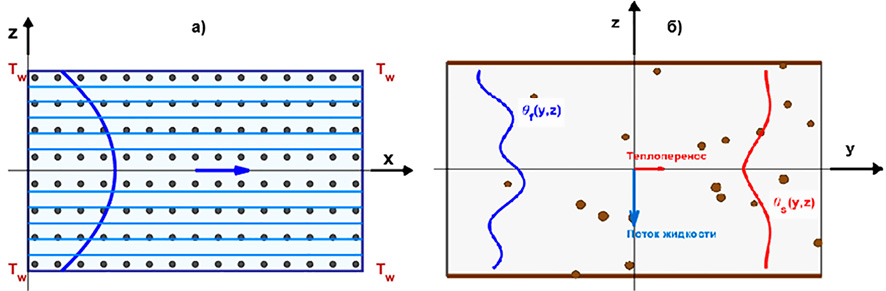
Рис. 1. Схема теплообмена в пористом прямоугольном канале: а) вид сверху, б) поперечный разрез Примечание: составлен авторами по результатам данного исследования
Гидродинамически развитое течение описывается моделью Бринкмана. Поле скорости имеет одну продольную компоненту u = u(y,z), определяемую уравнением [1]:
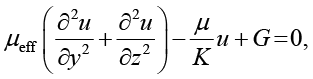(1)
где μ – динамическая вязкость жидкости (Па·с), μeff – эффективная вязкость (Па·с), K – проницаемость (м²), G = –dp / dx = const – постоянный градиент давления (Па/м). Граничные условия u = 0 при y = ±H, z = ±H соответствуют условию прилипания, а условия симметрии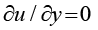 
при y = 0, 
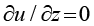при z = 0 отражают геометрическую симметрию задачи.
Решение уравнения (1) дает профиль скорости в виде произведения функций [1]:
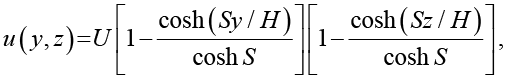(2)
где U – средняя скорость (м/с), а параметр S определяется как
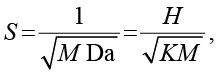
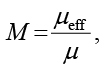
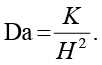
Здесь Da – число Дарси, а параметр S характеризует соотношение между сопротивлением пористой матрицы и вязкими силами; при S → 0 течение описывается моделью Дарси с плоским профилем, а при больших S профиль приближается к параболическому.
Теплообмен описывается системой уравнений энергии для каждой фазы с учетом вязкой диссипации по модели Дарси, где источник тепла пропорционален квадрату скорости. Для жидкости:
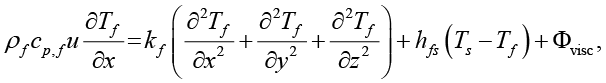(3)
для твердого каркаса, который считается неподвижным:
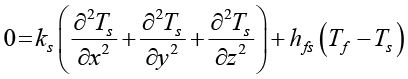, (4)
где ρf – плотность жидкости (кг/м³), cp,f – удельная теплоемкость жидкости (Дж/(кг·К)), kf – теплопроводность жидкости (Вт/(м·К)); ks – теплопроводность каркаса (Вт/(м·К)); hfs – объемный коэффициент межфазного теплообмена (Вт/(м³·К)). Источник диссипации задается моделью Дарси: Фvisc = μu2 / K (Вт/м³), что адекватно при малых числах Дарси (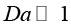
), когда доминирует сопротивление пористой среды.
Граничные и начальные условия формулируются следующим образом:
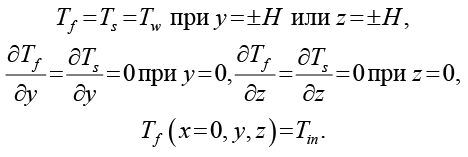(5)
Для перехода к безразмерному виду вводятся следующие переменные и параметры подобия:
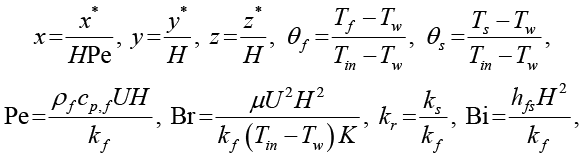(6)
где x*, y*, z* – размерные координаты (м), Pe – число Пекле, Br – число Бринкмана, kr – отношение теплопроводностей, Bi – число Био (параметр межфазного теплообмена).
Безразмерная система уравнений принимает вид
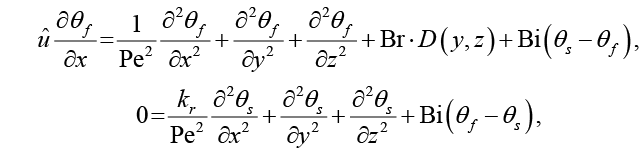(7)
где û = u / U, D(y,z) = û2. Граничные условия: θf = θs = 0 при y = ±1 или z = ±1; условия симметрии аналогичны (5); начальное условие: θf = 1 при x = 0.
Метод решения основан на разложении безразмерных температур в двойные ряды Фурье по полной системе собственных функций, удовлетворяющих граничным условиям на стенках:
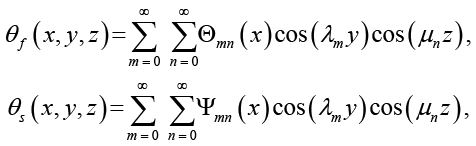(8)
где собственные значения λm = (2m + 1)π/2, μn = (2n + 1)π/2 обеспечивают выполнение граничных условий.
Подстановка (8) в (7) и применение процедуры разложения приводят к системе обыкновенных дифференциальных уравнений для амплитуд Θmn(x) и Ψmn(x). Для случая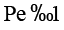 
продольной теплопроводностью в твердой фазе можно пренебречь, что дает алгебраическую связь:
(9)
Тогда уравнение для Θmn(x) принимает вид
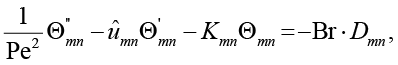(10)
где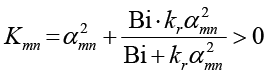 
, а коэффициенты Фурье ûmn и Dmn вычисляются через интегралы от профиля скорости (2).
Решение (10), ограниченное при x → ∞, имеет вид
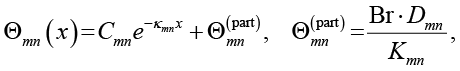(11)
где κmn > 0 – корень характеристического уравнения, а постоянная Cmn находится из начального условия.
На основе полученного решения определяется локальное число Нуссельта, характеризующее интенсивность теплообмена на стенке канала. С учетом вклада обеих фаз:
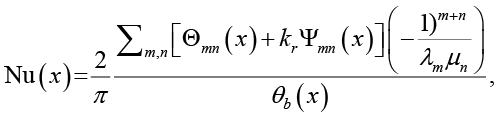(12)
где θb(x) – средняя объемная температура жидкости.
Результаты исследования и их обсуждение
На основе аналитического решения (8), (9), (11) и (12) выполнены расчеты тепловых и гидродинамических характеристик течения. Приняты следующие базовые параметры, если не указано иное: пористость ε = 0,5, kᵣ = 10, Br = 0,1, Bi = 1.
На рис. 2 представлены профили скорости. Как видно на рис. 2, а, с уменьшением числа Дарси (Da) профиль скорости приближается к параболическому (профилю Пуазейля в непористом канале). Для Da = 10-⁴ течение практически полностью описывается законом Дарси, профиль скорости выравнивается. Трехмерная структура поля скорости (рис. 2, б) и распределение его модуля в поперечном сечении (рис. 2, в) демонстрируют симметрию, характерную для геометрии прямоугольного канала.
Рис. 2. Профили скорости течения: а) влияние числа Дарси (Da) на безразмерный профиль u/U (сечение z = 0); б) трехмерное распределение скорости; в) контуры скорости в поперечном сечении (вид сверху) Примечание: составлен авторами по результатам данного исследования
Рис. 3. Результаты решения трехмерной задачи Гретца в локально-неравновесных условиях (Bi = 1, Br = 0,1): а) профили безразмерной температуры жидкости θf в сечении x = 0,1 при различных числах Пекле; б) изменение температуры θf(0,0) вдоль канала; в) изменение локального числа Nu(x) Примечание: составлен авторами по результатам данного исследования
Профили безразмерной температуры жидкости θf в сечении x = 0,1 (рис. 3, а) показывают классическую для задачи Гретца картину: с ростом числа Pe тепловой пограничный слой у стенок становится тоньше. Это связано с усилением роли конвективного переноса вдоль канала по сравнению с поперечным кондуктивным переносом. При малых Pe (Pe = 1) температура успевает выравниваться по сечению уже на небольшом расстоянии от входа.
Изменение температуры на оси канала θf(0,0,x) (рис. 3, б) подтверждает вывод: для Pe = 100 температура в центре падает очень медленно, что свидетельствует о большом расстоянии, необходимом для полного прогрева. При Pe = 1 температура быстро стремится к нулю.
В начальной точке (x → 0) число Nu стремится к бесконечности, что соответствует условию I рода на стенке при скачке температуры (рис. 3, в). Далее наблюдается монотонное уменьшение Nu по мере прогрева потока и выхода на термически развитый режим. Анализ показывает, что величина числа Pe существенно влияет на динамику числа Nu в начальной области, но слабо сказывается на его асимптотическом значении вдали от входа.
Заключение
В работе разработан аналитический метод решения, основанный на применении двойных рядов Фурье. Данный метод позволил получить в замкнутой форме решение для трехмерных полей температур жидкой и твердой фаз в пористом прямоугольном канале в рамках локально-неравновесной модели переноса тепла с учетом вязкой диссипации механической энергии.
Проведенный параметрический анализ на основе полученного аналитического решения позволил количественно оценить влияние ключевых безразмерных критериев, в первую очередь интенсивности межфазного теплообмена. Установлено, что переход от условий локального термического равновесия (Bi → ∞) к выраженному неравновесию (малые числа Био) приводит к значительному снижению – на 20–25 % – расчетного коэффициента теплоотдачи (числа Нуссельта) по сравнению с равновесным режимом. Показано также, что вклад вязкой диссипации в энергетический баланс становится сравнимым с конвективным переносом и определяет неадиабатический рост температуры жидкости вдоль канала при числах Бринкмана Br > 0,5.
Полученное решение обладает экспоненциальной сходимостью рядов и формирует строгий аналитический эталон. Эта работа вносит вклад в теорию сопряженного теплообмена и может служить для тестирования и верификации вычислительных алгоритмов, моделирующих сложные процессы теплопереноса в насыщенных пористых средах.
Конфликт интересов
Финансирование
Библиографическая ссылка
Губарева К.В., Еремин А.В. АНАЛИТИЧЕСКОЕ РЕШЕНИЕ ТРЕХМЕРНОЙ ЗАДАЧИ ГРЕТЦА В ПОРИСТОМ ПРЯМОУГОЛЬНОМ КАНАЛЕ В ЛОКАЛЬНО-НЕРАВНОВЕСНЫХ УСЛОВИЯХ С УЧЕТОМ ДИССИПАЦИИ // Современные наукоемкие технологии. 2025. № 12. С. 33-39;URL: https://top-technologies.ru/ru/article/view?id=40602 (дата обращения: 21.01.2026).
DOI: https://doi.org/10.17513/snt.40602