Введение
За последнее десятилетие беспилотные системы достигли значительных успехов, в основном благодаря растущему спросу на интеллектуальную автономность, устойчивую адаптивность и контекстно-зависимое принятие решений. Сегодня эти системы находят свое применение в самых различных областях и сферах деятельности, например таких, как автономное вождение, промышленная логистика, космические миссии и точное земледелие. Ключевым требованием для обеспечения производительности, надежности и безопасности беспилотных систем является точная характеристика их базовой динамики. В свою очередь, следует отметить, что достижение этой цели зависит от сочетания различных технологий, в том числе от решения особенно сложной задачи по разработке высоконадежных и безопасных систем искусственного интеллекта [1].
Эти системы должны быть способны ориентироваться в сложных условиях реального мира – будь то автомобиль, движущийся по загруженному городу, или самолет, совершающий посадку в неблагоприятных погодных условиях. Сложность заключается в том, чтобы обеспечить безупречную работу систем автономного вождения в любых условиях, что требует тщательного их тестирования на всех этапах производства с использованием наборов данных, точно отражающих критические сценарии. Именно поэтому в последние годы научно-исследовательские центры, лаборатории и ведущие производители все чаще обращают внимание на квантовые вычисления и, в частности, на квантовый генеративный искусственный интеллект как на технологию, которая имеет все необходимые характеристики для решения этой проблемы. Уже сегодня эксперты считают, что преимущества квантовых подходов могут идеально соответствовать потребностям создания систем автономного вождения и навигации. В отличие от классических, квантовые компьютеры способны обрабатывать огромные объемы данных и генерировать изображения с беспрецедентной детализацией и сложностью [2]. Эта способность открывает новые возможности создания точных симуляций критических тестовых сценариев, что необходимо для развития автономных технологий.
На рис. 1 показаны экспертные прогнозы относительно того, в каких сферах моделирования и производства беспилотных систем нейросетевые и квантовые технологии способны оказать наибольший эффект.
Несмотря на то, что более широкое применение и распространение квантовых компьютеров и интеллектуальных вычислительных методов в производстве может занять еще как минимум десятилетие, научно-экспертному сообществу уже сегодня целесообразно предпринимать шаги для лучшего понимания этих технологий и их потенциальных применений в технологических процессах выпуска беспилотных систем.
Таким образом, отмеченные обстоятельства подтверждают актуальность, теоретическую и практическую значимость темы данной статьи.
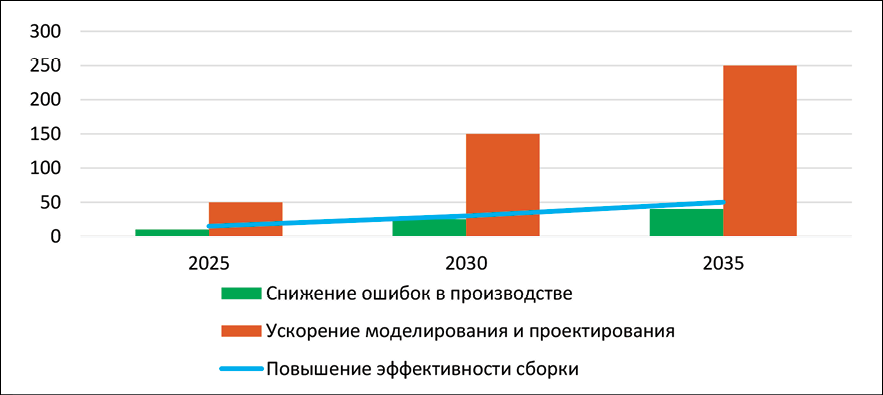
Рис. 1. Прогнозная динамика увеличения эффективности производства беспилотных систем с использованием нейросетевых и квантовых технологий (по сравнению с 2024 г., %) Примечание: составлено автором с использованием отчетов McKinsey & Company, Boston Consulting Group, DARPA, NVIDIA (The state of AI, Quantum computing’s P&L, AI in the Factory, Air Combat Evolution, DARPA, NVIDIA Omniverse, AI in Manufacturing)
Перспективы применения различных архитектур нейронных сетей для повышения точности и эффективности решения кинематических уравнений и управления роботами-манипуляторами в процессе производства сложных технологических систем рассматривают в своих трудах П.А. Замятин, Р.М. Ростовцев, С.А. Солохин, П.Е. Хрусталев [3], Zhang Youchun, Zhang Gongyong [4], Vandana Dabass, S. Sangwan [5].
Возможности квантового генеративного искусственного интеллекта для решения задачи разработки физической модели беспилотника, который позволит оптимизировать входные данные LiDAR и обрабатывать расстояния до препятствий, предупреждая тем самым столкновения и общую адаптивность, изучают М.Ф. Савельев, А.В. Обухов, Н.С. Малахова, Е.Г. Воробьев [6], М.Е. Иванов, Д. Решетников [7], Qifu Wang, Yuteng Guan [8].
Над усовершенствованием алгоритма на основе рекуррентной нейронной сети, который необходим для снижения вычислительных требований, обычно связанных с моделированием динамики беспилотных систем, трудятся Д.А. Сергеев [9], Nihar Patel, Nakul Vasani [10], Chunbo Zhao, Huaran Yan [11]. Особое внимание уделено требованиям к видеопотоку при FPV-управлении беспилотными системами [12].
В то же время в существующих на сегодняшний день публикациях освещены отнюдь не все аспекты интеграции квантовых вычислений и нейросетевых технологий в производственные процессы роботизированных платформ. Так, например, нерешенной остается проблема перевода дневных изображений дорог в ночные с сохранением контента, например, положения автомобилей. Эта задача особенно сложна из-за ресурсоемкости классических решений, которые часто дают нестабильные результаты. Отдельного внимания заслуживает вопрос преодоления трудностей, присущих квантовому машинному обучению, таких как проблема «плато Баррена», решение которого, по мнению ученых, будет крайне полезно для более точного проектирования объектов автономной мобильности.
Цель исследования – рассмотреть возможности и особенности применения нейросетевых и квантовых технологий в технологических процессах производства беспилотных систем.
Материалы и методы исследования
Включены анализ и синтез научных публикаций за 2022–2025 гг. в области применения нейросетевых и квантовых технологий в производстве беспилотных систем, систематизация данных международных отчетов (McKinsey & Company, BCG, DARPA, NVIDIA) о динамике внедрения инновационных технологий. Методы исследования: анализ и синтез, систематизация данных по сферам применения, моделирование с использованием физически информированных нейронных сетей, применение квантовых алгоритмов для оптимизации проектирования и производства, оценка эффективности и надежности автономных систем.
Результаты исследования и их обсуждение
Интеграция квантовых вычислений, технологий искусственного интеллекта в сферу беспилотных систем продвигается стремительными темпами. Эти передовые инновации стали трансформирующей силой в автономных платформах, предоставляя более действенные методы моделирования и испытаний, управления и оптимизации, с которыми классические приемы вычислений часто не справлялись. Междисциплинарные исследования изучают, каким образом квантовые технологии и нейронные сети могут улучшить автономные системы, решая сложные задачи, такие как планирование траектории, координация нескольких агентов, объединение датчиков и оптимизация. Сочетание квантовых вычислений с нейронными сетями улучшает производительность моделей за счет использования свойств квантовой механики, таких как суперпозиция, связанность и квантовый параллелизм [13].
На основе анализа имеющихся на сегодняшний день публикаций и результатов исследований автором в табл. 1 систематизирована информация относительно сфер приложений и возможностей использования рассматриваемых технологий.
Рассмотрим некоторые примеры приложения квантовых технологий и нейронных сетей в технологических процессах производства беспилотных систем.
Инжиниринг и проектирование
Инженерные симуляции имеют существенное значение для производства беспилотных систем. Они необходимы для сокращения затрат на проектирование и тестирование за счет уменьшения необходимости в физических прототипах и лабораториях, например, аэродинамических трубах в автомобильной и аэрокосмической отраслях. Численные моделирования, особенно основанные на методе конечных элементов, имеют решающее значение для симуляции сложных процессов, таких как аэродинамика, рабочая прочность, динамика конструкций, аварийная безопасность и производственные вопросы [14].
Таблица 1
Сферы и возможности применения нейросетевых и квантовых технологий в процессах производства беспилотных систем
|
Этап производства |
Нейросетевые технологии |
Квантовые технологии |
|
Проектирование и моделирование |
− оптимизация конструкции: нейросети могут анализировать тысячи вариантов дизайна для повышения аэродинамической эффективности и снижения веса; − прогнозирование поведения: симуляция поведения систем в различных условиях (ветер, осадки) для выявления и устранения уязвимостей |
− создание новых материалов: квантовое моделирование позволяет исследовать новые материалы с улучшенными свойствами (прочность, легкость); − оптимизация компоновки: квантовые алгоритмы могут находить наиболее эффективную комплектацию элементов на микроуровне, что улучшает производительность |
|
Разработка систем навигации и управления |
− автономная навигация: нейросети обрабатывают данные с сенсоров (камер, лидаров) для точного распознавания объектов и принятия решений в реальном времени; − адаптивное управление: система может самостоятельно подстраивать траекторию полета под меняющиеся условия (например, сильный ветер) |
− квантовые сенсоры: использование квантовых гироскопов и магнитометров для сверхточной навигации, не зависящей от GPS-сигналов; − оптимизация маршрута: квантовые алгоритмы могут мгновенно рассчитывать оптимальные маршруты, учитывая огромное количество переменных (препятствия, погодные условия) |
|
Распознавание и анализ данных |
− компьютерное зрение: мгновенное распознавание объектов, людей, животных, а также анализ местности для картографирования; − прогнозирование: анализ данных с датчиков для прогнозирования потенциальных угроз или неисправностей |
− улучшенная обработка сигналов: квантовые технологии могут обеспечить повышенную чувствительность сенсоров для обнаружения скрытых объектов или сигналов; − защита информации: использование квантовой криптографии для защиты каналов связи и предотвращения перехвата данных с беспилотника |
|
Контроль качества и безопасность |
− прогнозирование поломок: нейросети анализируют данные телеметрии и определяют вероятность отказа компонента; − автоматизированное тестирование: моделирование тысяч сценариев в виртуальной среде для проверки надежности системы |
− квантовые генераторы случайных чисел: обеспечение высокого уровня безопасности связи, что критически важно для защиты от взлома; − улучшенный контроль качества: использование квантовых сенсоров для обнаружения микроскопических дефектов в материалах, что повышает надежность аппарата |
Примечание: составлена автором.
Например, компания Bosch исследует подходы к моделированию электрических приводов беспилотных аппаратов на основе квантовых вычислений. AIRBUS изучает использование квантовых или гибридных квантово-классических подходов для вычислительной гидродинамики с целью сокращения затрат, необходимых для анализа поведения воздушного потока вокруг беспилотника.
Особое значение в данной сфере имеют физически информированные нейронные сети, которые вводятся для интеграции физических законов, обычно описываемых обыкновенными дифференциальными уравнениями (ОДУ), в глубокие нейронные сети (ГНС). Этот подход обучает ГНС в режиме контролируемого обучения для отслеживания и контроля заданных физических закономерностей, что позволяет автоматически находить решения ОДУ на основе данных. Основная идея физически информированной нейронной сети заключается в интеграции дифференциального уравнения в функцию потерь, как показано на рис. 2, что повышает надежность сети и облегчает точные аппроксимации даже в сценариях с недостатком данных, что очень часто встречается в технологических процессах производства беспилотных систем.
На рис. 2 условные обозначения:
− сплошные линии → это прямые причинно-следственные зависимости: данные, предсказания или вычисленные величины передаются от одного блока к другому;
− пунктирные линии → это обратные связи или адаптивные корректировки, другими словами, информация идет «назад» в сеть или в модуль коррекции, чтобы обновить веса, параметры или динамику;
− точечные линии → это слабые или вспомогательные связи, которые не участвуют напрямую в вычислительном процессе, но обеспечивают дополнительную проверку или учет информации (например, сравнение предсказаний с измерениями или влияние доверия на функцию потерь).
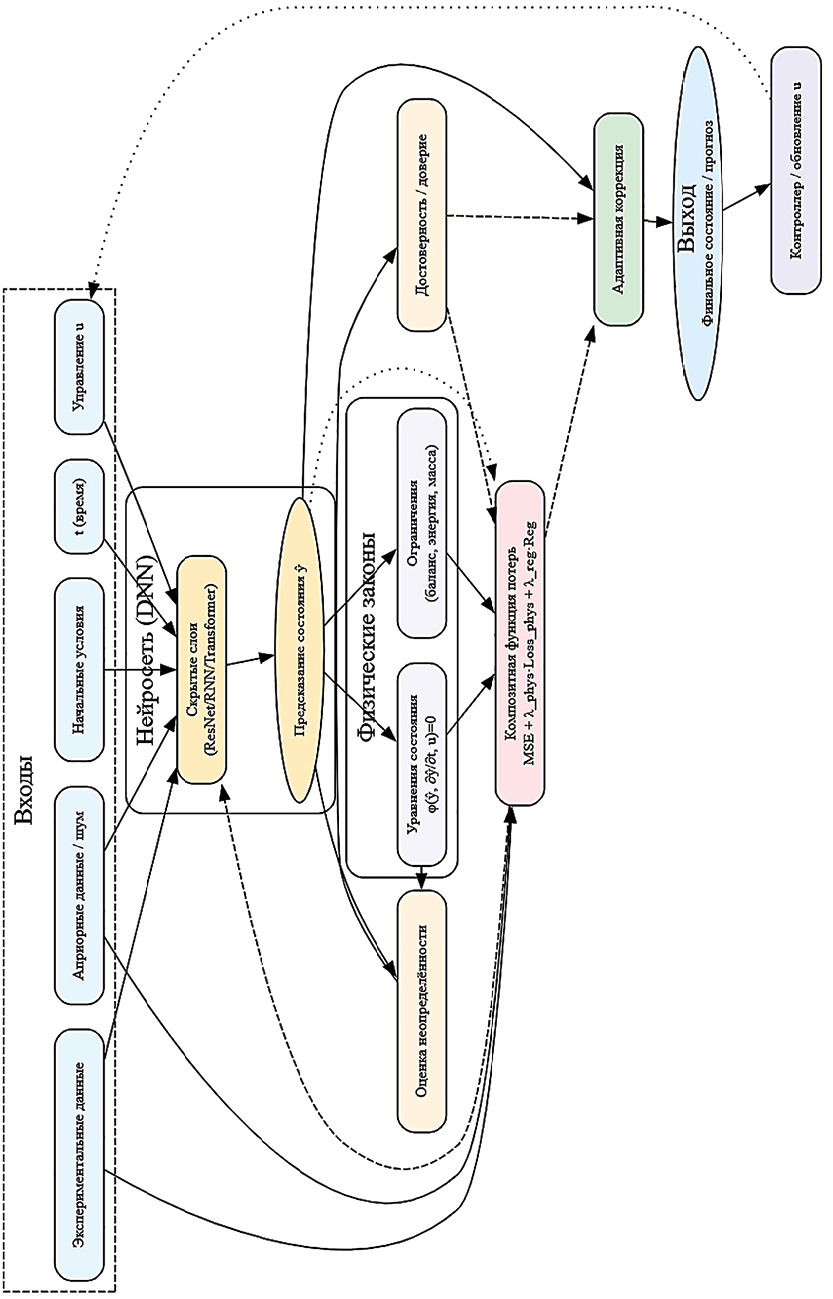
Рис. 2. Архитектура физически информированной нейронной сети Примечание: составлен автором по результатам данного исследования
Параметризованные и нелинейные уравнения в частных производных имеют следующий общий вид:
,
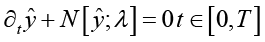где ŷ(t,x) представляет собой скрытое (неявное) решение или состояние динамической системы, а N[∙] обозначает нелинейный дифференциальный оператор, параметризованный λ. Определим l(t, x) как выражение в левой части уравнения, то есть:
.
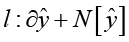После этого продолжается моделирование ŷ(t,x) с помощью глубокой нейронной сети. В данном контексте ŷ служит выходом многослойной нейронной сети, обозначенной lw(t), где ŷ = lw(t), пусть lw является функцией отображения, обученной глубокой сетью с адаптивными весами w. Таким образом, ожидается, что нейронная сеть обучится решению заданного ОДУ как функции непрерывного времени t.
Используя автоматическое дифференцирование и правило цепочки, можно вывести нейронную сеть, представляющую ŷ(t,x). Предполагая автономную систему, нейронная сеть ŷ(t) обучается, тем самым оптимизируются ее общие параметры с параметрами ŷ(t,x) и l(t,x). Цель – минимизировать функцию затрат среднеквадратичной ошибки (MSE).
,
,
,
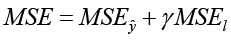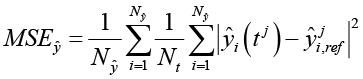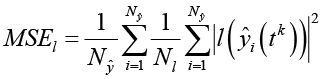где 0 ≤ γ ≤ 1 – гиперпараметр, который должен отражать степень уверенности в физических ограничениях системы, Nt – общее количество выборок обучающих данных, Nl – количество точек коллокации, а Nŷ – количество выходов, генерируемых нейронной сетью. Для каждого выхода i обозначаем прогноз сети как ŷi(∙). Имея пару данных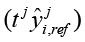 
, где j индексирует пару, а 
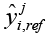является желаемым выходом, можно сравнить ее с прогнозом сети ŷi(∙).
Рассмотрим на конкретном примере преимущества использования архитектуры физически информированной нейронной сети для проектирования и производства БПЛА. Для этого проведем сравнительный анализ трех подходов: прямое численное моделирование, суррогатное моделирование на основе данных (Data-Driven Surrogate), физически информированная нейронная сеть (PINN).
Итак, задача заключается в параметрической оптимизации лонжерона крыла БПЛА.
Объект: лонжерон крыла БПЛА.
Параметр: толщина стенки лонжерона h.
Цель: минимизация массы m(h) при соблюдении ограничений по рабочей прочности.
Ограничение: максимальные эквивалентные напряжения (по Мизесу) σmax при расчетной аэродинамической нагрузке Fload не должны превышать допустимого значения [σ] = 250 МПа.
Сценарий: для построения функции отклика σmax(h) и нахождения оптимального h* требуется выполнить 100 оценочных расчетов (итераций) в диапазоне h ∈ [2,0 мм, 12,0 мм].
Подход 1: прямое численное моделирование (МКЭ)
Данный подход является традиционным и базовым для верификации. Он заключается в решении уравнений теории упругости методом конечных элементов (МКЭ) для каждой итерации hi(i = 1…100).
Методология: для каждого значения hi выполняется полный цикл: регенерация геометрии, дискретизация (построение сетки), решение системы линейных алгебраических уравнений (СЛАУ) KU=F и постобработка для нахождения σmax.
Вычислительная оценка:
− средняя вычислительная трудоемкость одного полного расчета (включая регенерацию сетки и решение) на доступном вычислительном кластере:
Tfem = 45 мин;
− суммарные вычислительные затраты на оптимизационный цикл:
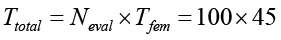мин = = 4500 мин = 75 ч.
Ограничение: подход вычислительно затратен и плохо масштабируется при увеличении числа параметров.
Подход 2: Суррогатное моделирование на основе данных (Data-Driven Surrogate)
Этот подход предполагает использование «чистой» нейронной сети (например, MLP – многослойный перцептрон) для аппроксимации функции отклика σmax ≈ f(h;w), где w – веса сети.
Методология: требуется двухэтапный процесс.
1. Этап «Offline» (генерация данных): создание репрезентативной обучающей выборки. Для адекватной аппроксимации нелинейной физики требуется Ndata точек, сгенерированных Подходом 1. Для обеспечения робастности предположим Ndata = 2000.
2. Этап «Online» (обучение и предсказание): обучение сети на выборке
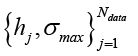
и последующее (предсказание) для 100 искомых вариантов hj.
Вычислительная оценка:
− затраты на генерацию данных:
Tdata = Ndata × Tfem = 2000×45 мин = 1500 ч;
− затраты на обучение сети:
Tdata ≈ 1 ч (на GPU);
− затраты на предсказание:
Tinfer < 1с.
Ограничение:
суммарные затраты Ttotal ≈ 1501 ч. Подход неэффективен для новых R&D задач, где отсутствует априорная база данных (data-scarce scenarios).
Подход 3: Физически информированная нейронная сеть (PINN)
Данный подход, описанный в статье, решает проблему дефицита данных, интегрируя физические законы (УЧП) непосредственно в функцию потерь.
Методология: сеть uNN(x,y,z,h,w) аппроксимирует само поле перемещений u в зависимости не только от координат (x,y,z), но и от параметра h.
Функция потерь Loss = Lossdata + Lossphys:
Lossdata: минимизирует ошибку на крайне малом наборе Nu «якорных» точек (результатов МКЭ-симуляций),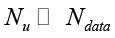 
.
Lossphys: минимизирует остаток УЧП теории упругости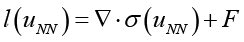 
на Nl точках коллокации, распределенных по области Ω и ее границам. УЧП выступает в роли регуляризатора.
Вычислительная оценка:
− затраты на генерацию данных: пусть Nu = 10 опорных симуляций (на 10 % меньше данных, чем в Подходе 1, и на 99,5 % меньше, чем в Подходе 2). Tdata = 10×45 мин = 7,5 ч;
− затраты на обучение сети: Ttrain_pinn. Обучение PINN – это нетривиальная задача оптимизации невыпуклой функции потерь, требующая тонкой настройки гиперпараметров (включая γ). Оценим ее в 5 ч;
− затраты на предсказание: Tinfer < 1 с.
Ограничение:
суммарные затраты Ttotal ≈ 12,5 ч. Сложность процесса обучения и чувствительность к гиперпараметрам (спектральное смещение, балансировка Loss).
Сравнительная характеристика полученных результатов представлена в табл. 2.
Сравнительный анализ показывает, что в задачах параметрической оптимизации, характеризующихся дефицитом данных, физически информированные нейронные сети (PINN) демонстрируют значительное (в представленном примере – в 6 раз) преимущество в вычислительных затратах по сравнению с традиционными методами прямого численного моделирования (75 ч vs 12,5 ч). В отличие от «чистых» суррогатных моделей, требующих для обучения очень больших объемов априорных данных (1501 ч), PINN эффективно используют информацию, заложенную в самих дифференциальных уравнениях (УЧП), которые выступают в роли мощного физического регуляризатора. Это позволяет находить достоверные решения даже при минимальном объеме эмпирических или численных данных (Nu), что полностью соответствует целям сокращения затрат на проектирование и производство БПЛА.
Таблица 2
Сводная таблица сравнительного анализа
|
Параметр |
Подход 1: прямой МКЭ |
Подход 2: суррогат (Data-Driven) |
Подход 3: PINN |
|
Основной принцип |
Численное решение УЧП |
Аппроксимация данных |
Гибрид: аппроксимация + регуляризация УЧП |
|
Потребность в данных (Ndata) |
0 (для предсказания) |
Ndata ~ 2000 + (для обучения) |
Nu ~ 10 (для калибровки) |
|
«Знание» физики |
Явное (встроен в решатель) |
Неявное (только из данных) |
Явное (встроено в Lossphys) |
|
Время «Offline» (подготовка) |
0 |
1500 ч (сбор данных) + 1 ч (обучение) |
7,5 ч (сбор данных) + 5 ч (обучение) |
|
Время «Online» (расчет 100 вариантов) |
75 ч |
< 1 с |
< 1 с |
|
Общее время выполнения |
75 ч |
~1501 ч |
12,5 ч |
Таблица 3
Применение квантовых алгоритмов для решения задач оптимизации технических процессов в ходе производства беспилотных систем
|
Алгоритм |
Математическая задача |
Техническое применение в производстве беспилотных систем |
|
Квантовый отжиг |
Комбинаторная оптимизация |
Оптимизация роботизированных сборочных линий: расчет идеальной последовательности операций для минимизации времени сборки. Проектирование печатных плат: размещение компонентов для максимальной эффективности и минимизации наводок |
|
Алгоритм Гровера |
Неструктурированный поиск данных |
Базы данных материалов: мгновенный поиск компонентов, соответствующих заданным техническим требованиям (прочность, вес, электропроводимость). Тестирование программного обеспечения: быстрый поиск уязвимостей или ошибок в коде полетного контроллера |
|
Квантовое моделирование |
Моделирование многочастичных систем |
Материаловедение: моделирование новых сплавов и композитов для корпусов с целью предсказания их прочности, усталости и теплопроводности на атомном уровне. Моделирование батарей: расчет химических реакций для разработки более эффективных и легких аккумуляторов |
|
Гибридные квантово-классические алгоритмы |
Оптимизация с ограничениями |
Оптимизация маршрутов и логистики: расчет идеальных маршрутов поставок с учетом тысяч переменных, таких как пробки, вес груза и срочность. Управление производством: оптимизация графика смен и использования оборудования для максимизации выпуска продукции |
|
Квантовые сенсоры (на основе кубитов) |
Сверхточное измерение |
Неразрушающий контроль: выявление микроскопических дефектов в материалах, сварных швах и электронике путем измерения магнитных и гравитационных аномалий. Калибровка: сверхточная калибровка гироскопов и акселерометров перед установкой. |
Примечание: составлена автором на основе полученных данных в ходе исследования
Производство и масштабирование
Технологические процессы производства беспилотных систем часто включают большое количество переменных и ограничений, которые необходимо учитывать. Классические алгоритмы, такие как имитационный отжиг, позволяют найти только локальные оптимумы и предоставить неоптимальное решение [15]. Квантовые подходы к оптимизации, такие как квантовый отжиг, адиабатические или гибридные алгоритмы (например, квантовый алгоритм приближенной оптимизации), обещают решить проблемы с большими пространствами параметров, предоставить более качественные решения и сократить время их поиска (табл. 3) [16].
Заключение
Активно развиваемые на сегодняшний день технологии искусственного интеллекта и квантовые вычисления заключают в себе большой потенциал повышения эффективности и точности технологических процессов производства беспилотных систем.
В рамках статьи описаны возможности использования метода машинного обучения на основе физических знаний, а именно нейронных сетей на основе физических знаний, для идентификации нелинейных моделей систем в процессе проектирования автономных платформ, особенно в случаях, когда реальные данные ввода-вывода ограничены. Показан потенциал физически информированных нейронных сетей в замене сложной нелинейной динамики более простыми и вычислительно эффективными аппроксимациями.
Проведенный сравнительный анализ вычислительной эффективности для задачи параметрической оптимизации лонжерона крыла БПЛА продемонстрировал значительное преимущество физически информированных нейронных сетей. Общие временные затраты на решение задачи (включая подготовку и расчет 100 вариантов) для PINN составили 12,5 ч, в то время как для традиционного прямого моделирования методом конечных элементов (МКЭ) потребовалось ~75 ч. Это 6-кратное ускорение достигается за счет замены многократных полных расчетов однократным обучением быстрой суррогатной модели.
Также в ходе исследования акцентировано внимание на повышенной сходимости, устойчивости к переобучению и стабильных результатах прогнозирования, которые могут быть достигнуты с помощью квантовых алгоритмов в процессе производства беспилотных систем и его масштабирования. Это представляет собой ценный шаг вперед в области высокоточной оценки и оптимизации динамических параметров в сложных системах, требующих точного моделирования в реальном времени.
Конфликт интересов
Благодарности
Библиографическая ссылка
Тырышкин С.Ю. ПРИМЕНЕНИЕ НЕЙРОСЕТЕВЫХ И КВАНТОВЫХ ТЕХНОЛОГИЙ В ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССАХ ПРОЕКТИРОВАНИЯ И ПРОИЗВОДСТВА БЕСПИЛОТНЫХ СИСТЕМ // Современные наукоемкие технологии. 2025. № 11. С. 143-151;URL: https://top-technologies.ru/ru/article/view?id=40578 (дата обращения: 12.12.2025).
DOI: https://doi.org/10.17513/snt.40578