Введение
Модели авторегрессии и интегрированного скользящего среднего (ARIMA) зарекомендовали себя как один из наиболее мощных и широко используемых инструментов для анализа и прогнозирования временных рядов в различных областях, включая экономику, финансы, инженерное дело и многие другие [1]. Их способность улавливать сложные зависимости и стохастические структуры в данных позволяет строить прогнозы с высокой степенью точности, что подтверждается многочисленными прикладными исследованиями [2-4].
Однако само по себе определение структуры модели ARIMA (порядков p, d, q) не гарантирует достижения оптимального прогностического результата [5]. Фундаментальную роль в эффективности модели играет корректный расчет ее коэффициентов – параметров авторегрессии (AR) и скользящего среднего (MA). Именно от точности этих оценок напрямую зависит, насколько адекватно модель будет описывать исследуемый стохастический процесс и, как следствие, насколько достоверными и надежными будут ее прогнозы.
В литературе представлено множество подходов к оценке параметров ARIMA, начиная от классического метода максимального правдоподобия (MLE) и заканчивая различными процедурами, такими как метод Ханнана – Риссанена (HR) [6] или методы, основанные на уравнениях Юла – Уокера (YW) [7]. Каждый из этих методов обладает своими особенностями, теоретическими свойствами, преимуществами и недостатками. Выбор конкретного алгоритма оценки может существенно повлиять не только на статистическую эффективность получаемых оценок и, соответственно, точность прогноза, но и на вычислительную сложность, а также на время, затрачиваемое на обучение модели.
Последний аспект – вычислительная эффективность – приобретает особую актуальность в современных условиях. С одной стороны, рост объемов данных требует масштабируемых алгоритмов и новый мощностей [8]. С другой стороны, существуют практические сценарии, где модели ARIMA необходимо реализовывать и эксплуатировать в средах с ограниченными вычислительными ресурсами или на платформах, где использование сложных итерационных процедур численной оптимизации, требующих специализированных математических библиотек, может быть затруднительным, неэффективным или даже невозможным. Примерами могут служить встраиваемые системы, некоторые корпоративные платформы или интерпретируемые языки программирования, где производительность итеративных вычислений существенно ниже, чем у компилируемого кода или нативных библиотечных функций. В таких условиях поиск и выбор оптимального, с точки зрения компромисса между прогностической точностью и вычислительной эффективностью, способа расчета коэффициентов ARIMA остается важной и не до конца решенной задачей.
Цель исследования – сравнительный анализ различных методов оценки параметров моделей ARIMA для прогноза продаж с акцентом на их прогностическую точность и вычислительную производительность, особенно в контексте возможной реализации на платформах с ограниченными возможностями для сложных численных расчетов. В частности, рассматривается возможность использования методов, сводящихся к решению систем линейных алгебраических уравнений (СЛАУ), что позволяет задействовать оптимизированные встроенные решатели, если таковые имеются на целевой платформе. В качестве тестовой целевой платформы рассматривается 1С, которая имеет в себе встроенный оптимизированный решатель СЛАУ.
Сравнение проводится на наборе синтетических временных рядов, а также на данных из международного конкурса прогнозирования M4, что позволяет оценить надежность выводов. Были взяты месячные данные из оригинального датасета M4 competition [9]. Серия открытых M-соревнований, инициированная С. Макридaкисом, служит крупнейшим эмпирическим полигоном для сравнения методов прогнозирования временных рядов. За период с 1982 по 2024 год проведено шесть раундов. Для сравнения были взяты четвертые соревнования, как последние, которые проводились в основном без нейросетевых методов [10]. В контексте M-соревнований стандартными бенчмарками считаются автоматизированные ARIMA (auto.arima), ETS и Theta, современное изложение которых представлено в [11]. Однако в данной работе мы фокусируемся на сравнивании оценивателей параметров в ARIMA, а не на межсемейном сравнении методов прогнозирования.
Материалы и методы исследования
В статье исследуются четыре метода: метод максимального правдоподобия (MLE), метод Ханнана – Риссанена (HR), комбинированный метод Юла – Уокера и регрессии Дурбина (YW+Durbin), а также предложенный автором подход, основанный на двукратном применении уравнений Юла – Уокера (YW2). Краткое описание методов представлено в таблице 1.
Реализации методов. Для сравнения точности использовались реализации на Python 3.12 (NumPy 1.26, SciPy 1.15, statsmodels 0.14). Оценка MLE выполнена в state-space формулировке (фильтр Калмана) средствами statsmodels. Оптимизатор – L-BFGS-B, maxiter=50, прочие параметры – значения по умолчанию statsmodels 0.14. Метод HR реализован двухшагово: предварительная AR(m), далее OLS по лагам ряда и остаткам; линейные задачи решались через SVD (numpy.linalg.svd). Схемы YW+Durbin и YW2 решали соответствующие системы линейных уравнений методом наименьших квадратов (numpy.linalg.lstsq). Для сравнения скорости методы HR и предложенный YW2 дополнительно реализованы на платформе 1С. Системы линейных уравнений решались встроенным решателем платформы, SVD вычислялась по ручной реализации алгоритма Голуба – Рейнша.
Таблица 1
Описание методов расчета коэффициентов ARIMA
|
Обозначение |
Метод |
Краткая идея |
Тип вычислений |
|
MLE |
Максимальное правдоподобие |
Совместная оптимизация p, q коэффициентов и дисперсии через функции правдоподобия |
Нелинейные итерации, градиенты [12] |
|
HR (МНК-SVD) |
Метод Hannan-Rissanen через МНК. МНК рассчитывается через сингулярное разложение |
1. Оценивается длинная AR(m) модель. 2. Оценивается полная ARMA (p,q) модель с помощью МНК через лаги исходного ряда и лаги остатков с первого шага |
Две линейные итерации по расчету МНК |
|
YW + Durbin |
Yule–Walker (YW) на AR-части → регрессия Дурбина на MA |
1. Решить систему YW для φi. 2. Оценить θj из остатков с помощью обратной регрессии |
Две линейные системы |
|
YW2 (предложено автором) |
Yule–Walker на AR, затем повторно Yule–Walker на остатках |
1. AR как выше. 2. Новая YW-система для остатков → θ |
Две линейные системы |
Источник: составлено автором.
Кратко охарактеризуем эти методы. MLE даёт асимптотически несмещённые и эффективные оценки, но чувствителен к начальным условиям и требует многократного инверсионирования ковариационной матрицы (O(T·(p + q)2)) [13].
HR алгоритм представляет собой двухэтапную процедуру оценки параметров моделей ARMA. На первом этапе метод оценивает чистую авторегрессионную модель высокого порядка для исходного временного ряда, получая предварительные остатки [14]. На втором этапе осуществляется МНК-оценка полной ARMA-модели, с использованием лаговых значений ряда и полученных остатков в качестве регрессоров, что позволяет линеаризовать исходно нелинейную по параметрам MA-составляющую. Основные преимущества метода включают вычислительную простоту, возможность распараллеливания и отсутствие необходимости в итеративной оптимизации для базовой оценки [15]. Однако данный метод имеет ряд недостатков по сравнению с процедурами максимального правдоподобия. Во-первых, получаемые оценки являются асимптотически неэффективными, особенно для моделей с сильной MA-компонентой, что приводит к более широким доверительным интервалам параметров. Во-вторых, метод проявляет значительную чувствительность к выбору порядка предварительной AR-аппроксимации, что может вызвать смещение итоговых оценок. МНК задача на втором шаге решается через SVD-разложение матрицы регрессоров для численной устойчивости. Хотя МНК не гарантирует статистическую эффективность для ARMA-процессов, его комбинация с SVD позволяет получать надежные оценки даже при наличии мультиколлинеарности [16] в регрессорах и не требует предположений о нормальности ошибок.
YW+Durbin. Основная идея – заменить нелинейную задачу оценки ARMA (p, q) двумя линейными регрессиями – сначала на исходном ряду, потом на полученных остатках. Решается через построение длинной AR(m) модели, расчета остатков и вычисления OLS регрессии с остатками и коэффициентами с первого шага. Матрица размера m x m рекурсией Левинсона за O(m2); регрессия – O(T(p+q)). Для типичных m≤15 это почти линейно по длине ряда [17].
YW2 (Двойной Yule – Walker). Суть метода сводится к двум последовательным применениям уравнений Юла – Уокера. Первое приближает весь процесс длинной AR(m)-моделью, второе ищет оставшуюся корреляцию в остатках. Это аппроксимационный подход к оценке параметров ARMA(p,q) модели. Можно предположить, что остатки AR(m)-аппроксимации ARMA(p,q) процесса сами являются некоторым ARMA-процессом. Применение к ним YW-уравнений – это попытка оценить их AR-часть и использовать её как MA-коэффициенты для исходной модели ARIMA. Главное отличие от метода YW+Durbin в том, что здесь используются системы линейных уравнений в двух шагах, а в YW+Durbin только в первом.
Данный метод можно представить в виде следующих шагов:
1) оцениваем AR(m):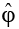 
= R–1r, где R – матрица автокорреляций;
2) вычисляем остатки: εt = yt – ∑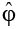 
iyt–i ;
3) применяем YW к остаткам: θ = Rε–1rε .
YW2 трактует ARMA(p,q) как AR(m)-аппроксимацию с «остаточной» корреляцией, которую затем повторно моделирует Yule – Walker на остатках. Это даёт две линейные задачи вместо нелинейной оптимизации MLE и двухступенчатой регрессии HR (с SVD), что позволяет полностью остаться в Toeplitz-системах и использовать их численные преимущества в средах вроде 1С. Первый и второй шаги YW2 сводятся к решению Toeplitz-систем, их устойчивое решение обеспечивается внутренними алгоритмами платформы 1С. Модели с единичными корнями пропускались, в таком случае использовалась топ 2 модель перебора по сетке.
При завышенном m оценки могут быть смещёнными из-за утечки структуры MA в первую AR-аппроксимацию; однако при умеренных m и достаточном T смещение уменьшается, а повторное применение YW к остаткам позволяет частично «возвратить» MA-составляющую. На практике это подтверждается тем, что на M4-рядах методы дают сопоставимый MAPE, то есть возможное смещение YW2 не транслируется в значимое ухудшение прогноза.
YW2 относится к двухшаговым моделям. По сравнению с методом Дурбина, YW2 проще интегрируется в производственные контуры 1С: оба шага сводятся к Toeplitz-СЛАУ, что обеспечивает детерминированность и скорость при массовой обработке серий. Методы на основе инноваций/точного правдоподобия (state-space/Kalman-innovations, MLE) обычно дают наилучшие оценки при сильной MA-составляющей и на коротких рядах, но требуют итерационной оптимизации и аккуратной инициализации параметров [18], что не является практически целесообразным в ресурсоограниченных средах. Частотный критерий Уиттла (Whittle) – быстрая асимптотическая альтернатива для очень длинных стационарных рядов, на коротких выборках может давать смещение [19]. Метод Берга (Burg) применим прежде всего к AR-моделям: он обеспечивает устойчивость (все корни вне единичного круга) и хорош для быстрой AR-аппроксимации/предобработки, но не идентифицирует MA-часть сам по себе [20]. В нашей прикладной постановке (массовые расчёты в 1С с ограниченными ресурсами) приоритет отдан YW2; Durbin используется как резервный метод. Реализация Innovations/Whittle/Burg не включалась именно из-за фокуса на быстром решении линейных систем (где 1С сильна).
Ограничения применяемого пайплайна. Реализация механизма в 1С сознательно минимизирует зависимость от итерационных процедур и тяжёлой линейной алгебры. В базовой конфигурации использованы фиксированные d=1 и, при наличии сезонности, D=1 (сезонные P и Q в данной статье не вычислялись). В прикладных розничных данных со структурными сдвигами и трендом d=1 – разумное «безопасное» значение, которое снижает систематические ошибки тренда без существенного ухудшения на стационарных сериях. Дополнительные порядки дифференцирования в прототипе давали худшую устойчивость коэффициентов и рост дисперсии ошибок. Автотесты ADF/KPSS не применялись из-за сложности и стоимости их реализации в 1С.
Порядок AR(m) выбран по эвристике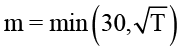 
, авторы модели HR в [14] рекомендуют использовать функцию определения порядка p, которая растет быстрее, чем log(n), но медленнее, чем log(n)2. Для типичных длин рядов это даёт качественную при приемлемой трудоёмкости: сложность шага Yule – Walker растёт приблизительно как O(m²). Формула гарантирует рост m медленнее, чем линейно от n, и тем самым стабилизирует время расчёта на больших рядах. Систематическое исследование влияния m на точность и стабильность выходит за рамки данной статьи и запланировано как отдельная работа.
Выполнялась проверка на единичные корни для коэффициентов MA. Коэффициенты AR не проверялись, так как метод Юла – Уокера, исходя из своих свойств положительно определенной матрицы автоковариаций, всегда возвращает стационарное решение [21]. Проверка MA коэффициентов выполнялась по формуле: sum(θq) > 1. При условии q = 1 эта проверка является необходимой и достаточной, при q = 2...3, она является первым приближением. Сделано так для экономии вычислительных ресурсов, с учетом того, что уже проводится перебор по сетке, который в большинстве случаев отбраковывает модели с единичными корнями.
Результаты исследования и их обсуждение
Тестирование проводилось в два этапа, что позволило максимально приблизить условия эксперимента к реальным задачам розничного бизнеса и одновременно обеспечить воспроизводимость результатов. Общая схема эксперимента представлена в таблице 2.
На всех этапах целевой показатель точности – MAPE.
Таблица 2
Структура эксперимента для регулярных продаж
|
Этап |
Источник рядов |
Кол-во рядов |
Цель |
|
I |
Синтетические ряды (12 сценариев) |
12 x 60 = 720 |
Проверка моделей на контролируемых паттернах и параметрическая отладка |
|
II |
Набор M4 (подвыборка месячных рядов) |
720 |
Сравнение с результатами международного соревнования M4 competition и проверка на «живых» данных |
Источник: составлено автором.
Для этапа I был разработан генератор simulate_series на Python 3.12 (библиотеки NumPy 1.26, SciPy 1.15, statsmodels 0.14). Он имитирует регулярные продажи, комбинируя:
1. Тренд – детерминированный (аддитивный / мультипликативный) и стохастический локально-линейный (случайный дрейф уровня L и наклона b).
2. Сезонность – Фурье-разложение с периодом 12 месяцев и 1 гармоникой; амплитуда регулируется параметром seas_amp.
3. Случайное возмущение – процесс AR(1) с коэффициентом автокорреляции φ и шумом σε.
4. Разовые выбросы и «обнуления» – разовые выбросы (p_out, out_scale) и искусственные нулевые продажи (zero_p) для моделирования сезонных пауз или отсутствия спроса.
5. Когерентность типа ошибок – возможность переключения между аддитивной и мультипликативной схемой формирования итогового ряда (multiplicative).
Каждый сгенерированный ряд округлялся до целых значений, что типично для товаро-учётных систем.
Были предложены двенадцать сценариев (S1–S12), охватывающих основные сочетания тренда, сезонности, шумов и выбросов, характерные для розницы:
− S1–S3. Детерминированный аддитивный тренд, без/с умеренной/сильной сезонностью; рост шума и появление выбросов в S3.
− S4–S6. Мультипликативный тренд с коррелированным шумом (φ = 0.6); амплитуда сезонности 0 / 10 / 30.
− S7–S9. Стохастический аддитивный тренд; вариация сезонной амплитуды и шума.
− S10. Комбинация аддитивного тренда, сильной сезонности и AR-шумов.
− S11. Мультипликативный тренд с сильной сезонностью и выбросами (имитация акционных продаж).
− S12. Самый «неустойчивый» сценарий: стохастический тренд + сильная сезонность + AR шум + выбросы.
Каждый сценарий генерировал 60 независимых рядов длиной 120 месяцев. Разные стартовые зерна (seeds) генератора случайных чисел обеспечивали статистическую независимость, а их сохранение позволяет воспроизвести результаты. Для каждого ряда и для каждого из четырех методов порядок модели (p, q) определялся независимо путем перебора по сетке (p от 1 до 10, q от 0 до 3) с целью минимизации MAPE на валидационной выборке. Такой подход позволяет избежать смещения в пользу какого-либо одного метода и обеспечивает справедливое сравнение их. Данные разделялись на обучающий и тестовый отрезок. Прогноз строился на 6 месяцев.
Чтобы убедиться, что результаты не являются артефактом синтетики, модели прошли дополнительную валидацию на M4-подвыборке (720 месячных рядов). Использована метрика MAPE. Для избегания нулей применялся эпсилон-сдвиг. Эпсилон рассчитывается как 5% от среднего в ряде. Учитывая разнородную структуру датасета, разные по природе и длительности ряды, был введен практический критерий значимости – разница более 2 п.п. по метрике. Дополнительно оценивалась скорость работы (wall time) для всех алгоритмов.
Результаты и их интерпретация представлены в таблицах 3 и 4.
Итого: MLE практически всегда проигрывает, уступая лидеру на 2–5 п.п. Он опередил один из YW-методов лишь эпизодически (S3, 9, 10, 12) и в среднем на 1.56 п.п. хуже HR.
HR является самым точным методом на синтетических данных. Его отрыв от ближайшего преследователя составляет в среднем 0.74 п.п. MAPE и превышает 1 п.п. в пяти «тяжёлых» сценариях, где присутствуют сильные сезонные колебания или выбросы.
YW + Durbin и YW2 поделили второе место. Их средние MAPE совпадают (разница 0.002 п.п.). YW + Durbin чуть устойчивее в сценариях с шумом/выбросами (S3, 12), тогда как YW2 слегка лучше на «ровных» рядах (S1, 4).
Таблица 3
Результаты сравнений методов, MAPE
|
Сценарий |
MLE |
HR (МНК) |
YW + Durbin |
2x YW |
|
S1 |
4,01 |
2,95 |
3,43 |
2,96 |
|
S2 |
8,69 |
6,09 |
7,45 |
7,92 |
|
S3 |
12,34 |
10,53 |
14,75 |
15,41 |
|
S4 |
7,22 |
5,07 |
5,37 |
5,13 |
|
S5 |
9,19 |
7,33 |
8,66 |
8,61 |
|
S6 |
10,28 |
7,85 |
9,09 |
8,10 |
|
S7 |
8,85 |
8,34 |
8,38 |
8,40 |
|
S8 |
8,84 |
7,80 |
8,66 |
8,67 |
|
S9 |
9,47 |
8,92 |
12,88 |
13,47 |
|
S10 |
11,22 |
9,88 |
11,58 |
11,35 |
|
S11 |
12,04 |
8,71 |
10,08 |
9,98 |
|
S12 |
12,61 |
12,59 |
12,86 |
13,14 |
|
Среднее |
9,56 |
8,01 |
9,43 |
9,43 |
Источник: составлено автором.
Таблица 4
Интерпретация результатов
|
Сценарии |
Краткое описание |
Δ MAPE HR ↔ 2YW |
|
S1, 4, 6, 7, 8, 12 |
Простые тренды (аддитивные / мультипликативные) и/или слабый шум |
≤ 0.26 п.п. |
|
HR S2, 3, 5, 10, 11 |
Умеренная/сильная сезонность, выбросы, AR-шум или их комбинация |
1.27–1.81 п.п. |
Источник: составлено автором.
Таблица 5
Средний MAPE методов по всем рядам
|
Модель |
MAPE |
sMAPE |
Δ к лидеру (abs / %) |
|
YW + Durbin |
6.25 |
6.22 |
– |
|
Hannan – Rissanen |
6.46 |
6.57 |
+0.21 / +3.5% |
|
MLE |
6.55 |
6.29 |
+0.30 / +4.8% |
|
YW2 |
6.76 |
6.77 |
+0.51 / +8.4% |
Источник: составлено автором.
HR выигрывает на синтетических данных за счет регуляризации. Длинная AR-аппроксимация + OLS на остатках усредняют шум и снижают риск переобучения, что критично в коротких (N = 120) синтетических выборках.
Средний MAPE HR 8.0 п.п. против 9.4 п.п. у ближайших конкурентов и 9.6 п.п. у MLE. Выигрыш HR является статистически значимым (Friedman (N=12, k=4), p ≈ 0.01), но его абсолютная величина остаётся умеренной (≈ 0.7 п.п.). Это подтверждает, что преимущество HR объясняется не специфичностью рядов, а устойчивостью трёхшаговой процедуры, особенно заметной в «трудных» сценариях с сезонностью и выбросами. Попарный тест Неменьи показывает статистическое отличие метода HR от остальных. При этом все остальные методы попарно статически неотличимы, p > 0.7.
Теперь перейдем к рассмотрению данных M4. В таблице 5 представлены результаты тестов на подвыборке М4. Дополнительно была взята метрика sMAPE для возможности сопоставления с официальными результатами M4.
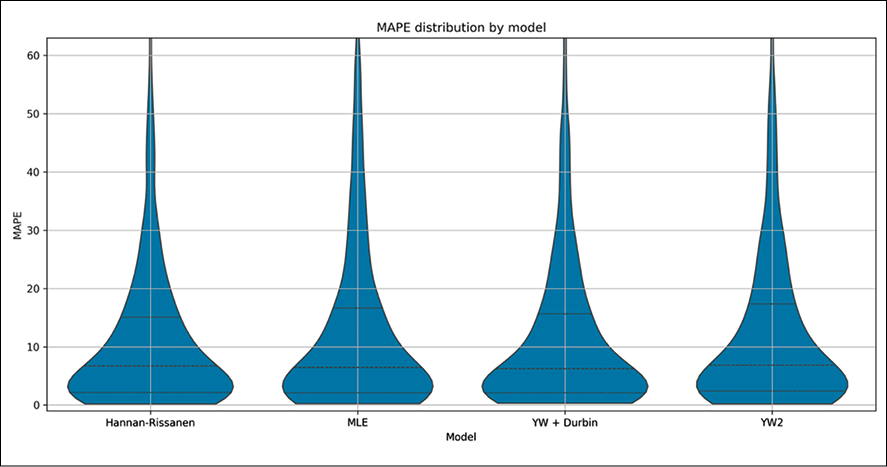
Распределение MAPE Источник: составлено автором
Таблица 6
Время расчета прогноза в 1С
|
Модель |
Количество рядов |
Время (с) |
|
HR |
36 |
16 |
|
YW2 |
36 |
3 |
|
HR |
220 |
80 |
|
YW2 |
220 |
7 |
Источник: составлено автором.
Средняя попарная разница между моделями ≈ 0.34 MAPE-п.п.; максимум (лидер ↔ аутсайдер) – 0.51. Максимальная дельта ниже порога практической значимости – 2 п.п. Результаты по sMAPE демонстрируют похожие результаты.
Для формальной оценки различий мы провели попарные тесты Уилкоксона с поправкой Бонферрони (порог α ≈ 0.0083). Тесты выявили, что предложенный метод YW2 статистически значимо уступает альтернативам: HR (p < 0.0001), YW+Durbin (p < 0.0001) и MLE (p = 0.0015). В то же время HR и YW+Durbin оказались статистически неразличимы (p = 0.684), как и пары MLE-HR (p = 0.011) и MLE-YW+Durbin (p = 0.021).
Результаты теста показывают, что не все методы статистически эквивалентны. Этот статистический вывод необходимо сопоставить с практической значимостью. Как показано в таблице 5, разница в среднем MAPE между лидером (YW+Durbin, 6.25 п.п.) и YW2 (6.76 п.п.) составляет всего 0.51 п.п. Эта величина, будучи статистически реальной, находится значительно ниже установленного порога практической значимости в 2 п.п. Это позволяет сделать ключевой вывод: метод YW2 обеспечивает практически сопоставимую точность с лучшими аналогами, жертвуя небольшой, практически незначимой долей точности в обмен на кардинальное (порядка 10 раз, табл. 6) ускорение вычислений в целевой среде 1С.
На рисунке представлен график распределения MAPE в зависимости от модели. Все модели показывают схожее распределение и границы 25/50/75 перцентиля.
В качестве тестирования в прикладном решении, модели HR и YW2 были реализованы на языке 1С. Для решения систем линейных уравнений использовался специализированный модуль, существующий в платформе 1С. Результаты тестирования времени представлены в таблице 6. Для замеров использовалась платформа 1С версии 8.3.25 (x64) в файловом варианте работы. Использовалась виртуальная машина с ОС Windows 11 (x64), 6 vCPU, 12 ГБ ОЗУ, NVMe SSD. Для каждого теста выполнено 3 замера, в таблице представлены средние значения.
Как видно из таблицы 6, при использовании специализированных (программных или аппаратных) модулей для расчета систем линейных уравнений предложенный метод YW2 показывает значительное ускорение времени выполнения.
Ускорение YW2 объясняется тем, что HR требует SVD-разложения матрицы размера Tx(p+q+m), что имеет сложность O(T·(p+q+m)²). При этом YW2 решает две системы размера mxm, что при использовании специализированных модулей работает за O(m²). При T >> m (типично для временных рядов) разница становится критической.
Различие результатов на синтетических и реальных данных подчеркивает важность валидации на практических задачах. HR показал преимущество на структурированных синтетических рядах благодаря регуляризации через длинную AR-аппроксимацию. Однако на зашумленных реальных данных M4 это преимущество нивелировалось, что делает выбор метода зависимым от вычислительных ограничений платформы.
Заключение
Целью иследования был поиск оптимального по соотношению точность/время вычислений метода расчета коэффициентов ARIMA.
На синтетических данных с выраженной структурой лучшую точность показал метод HR. Однако на реальных данных из M4 все методы (MLE, HR, YW+Durbin, YW2) продемонстрировали статистически неотличимую и практически эквивалентную точность (разница в среднем MAPE < 0.5 п.п.). В то время как на контролируемых синтетических данных метод HR показал статистически значимое преимущество, на более разнообразном и зашумленном наборе реальных данных M4 его преимущество исчезло. Это говорит о том, что в реальных условиях точность всех рассматриваемых линейных методов становится сопоставимой, и на первый план выходит вычислительная эффективность. Тестирование в целевой среде (1С) показало, что методы, сводящиеся к решению СЛАУ (YW2), на порядок (~10 раз) быстрее более сложных процедур (HR).
В качестве направлений дальнейших исследований запланирован анализ различных формул определения порядка m для первого шага YW2, анализ эффективности прогноза на различных горизонтах.
Предложенный метод YW2 является оптимальным выбором для исследуемой предметной области. Он обеспечивает точность прогнозирования на уровне лучших альтернатив (включая MLE) на реальных данных, но при этом обладает значительно более высокой вычислительной производительностью. Этот компромисс делает его идеальным кандидатом для встраивания в системы, где критична скорость расчета, используются медленные языки, имеются специализированные методы для ускоренного вычисления систем линейных уравнений, либо ограничены вычислительные ресурсы.
Генератор рядов, его используемые конфиги, сиды и ID рядов из набора M4 представлены в архиве на Harvard Dataverse [22].
Конфликт интересов
Библиографическая ссылка
Брыкин Д.О. МЕТОДЫ ОЦЕНКИ ПАРАМЕТРОВ ARIMA: СРАВНИТЕЛЬНЫЙ АНАЛИЗ ТОЧНОСТИ И ВЫЧИСЛИТЕЛЬНОЙ ЭФФЕКТИВНОСТИ // Современные наукоемкие технологии. 2025. № 10. С. 17-25;URL: https://top-technologies.ru/ru/article/view?id=40522 (дата обращения: 15.11.2025).
DOI: https://doi.org/10.17513/snt.40522