Введение
Методы оценки абитуриентов зачастую характеризуются недостаточной точностью и объективностью, что ведет к ошибочному отбору студентов и снижению их академической успеваемости [1]. На фоне усиления конкуренции между вузами и сокращения числа поступающих актуализируется необходимость оптимизации системы отбора [2]. Неточности в оценках повышают для абитуриентов риск выбора образовательной программы или вуза, не соответствующей их потребностям, что ухудшает успеваемость и снижает удовлетворенность учебным процессом [3, 4]. В связи с этим абитуриенты стремятся получить уверенность в том, что выбранное направление поможет достичь как академических, так и профессиональных целей.
Цель исследования – прогнозирование успеваемости студентов на основе сравнительного анализа и оптимизации теоретических моделей машинного обучения для повышения точности оценки их академических результатов.
Основное внимание в исследовании уделяется следующим задачам:
1. Описание данных и их нормализация.
2. Описание оценочных метрик.
3. Описание каждой созданной модели.
4. Сводная таблица с оценками моделей.
В результате проведения исследования авторы ставили гипотезу о возможности прогнозирования будущей успеваемости абитуриента в вузе по выбранной специальности, на этапе окончания им школы и наличия только оценочных «объективных» результатов школьной успеваемости, без учета личностных качеств абитуриента и школьной жизни.
Материалы и методы исследования
В исследовании используются данные по 1662 студентам направления 09.03.01 «Информатика и вычислительная техника». Исходные данные включают в себя оценки по 17 школьным предметам, средний балл за школьный аттестат, результаты ОГЭ и ЕГЭ по математике, результат ЕГЭ по физике [5], а также вузовскую оценку за выпускную квалификационную работу (ВКР) и вузовскую среднюю экспертную оценку всех преподавателей выпускающей кафедры.
Данные распределены следующим образом. Входными данными являются оценки по школьным предметам, которые включают алгебру, геометрию, физику, информатику, русский язык, литературу, историю, биологию, химию, обществознание, географию, физическую культуру, иностранный язык, основы безопасности жизнедеятельности (ОБЖ), музыку, изобразительное искусство (ИЗО), технологию, средний балл за школьный аттестат по всем предметам, результаты ОГЭ по математике (все эти баллы в диапазоне оценок от 3 до 5). Также учитываются входные данные в виде результатов ЕГЭ по математике и по физике [6] (диапазон баллов от 40 до 100). Выходными данными являются оценки за ВКР и средняя экспертная оценка преподавателей (подробнее формирование оценки описано в статье [4]) с диапазоном баллов от 61 до 100. Фрагмент имеющихся данных изображен на рис. 1.
Для улучшения качества моделей и повышения точности прогнозирования все данные были нормализованы. Нормализация данных была выполнена с использованием библиотеки scikit-learn и ее класса StandardScaler, который стандартизирует данные, приводя их к нормальному распределению с нулевым средним и единичным стандартным отклонением [7].
Процесс стандартизации включает следующие шаги:
1. Вычисление среднего значения и стандартного отклонения для каждого признака. Среднее значение (mean) и стандартное отклонение (standard deviation) вычисляются по каждому признаку на обучающей выборке [8].
2. Трансформация данных. Для каждого признака выполняется операция, описываемая формулой
z = (x – μ) / σ, (1)
где x – значение признака, μ – среднее значение признака, σ – стандартное отклонение признака.
Фрагмент нормализованных данных изображен на рис. 2.
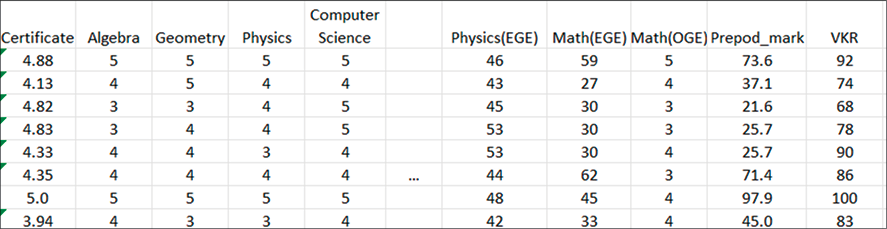
Рис. 1. Фрагмент исходных данных
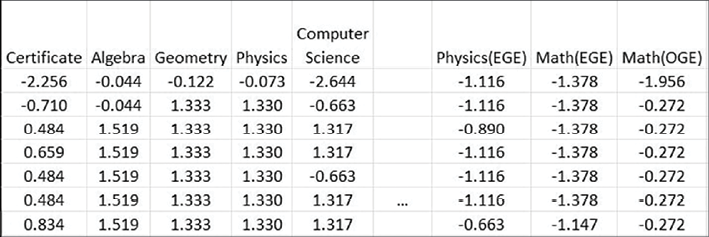
Рис. 2. Фрагмент нормализованных данных
Для оценки производительности моделей машинного обучения в рамках данного исследования используются следующие основные метрики: среднеквадратичная ошибка (Mean Squared Error, MSE), коэффициент детерминации (R² или R-squared), средняя абсолютная ошибка (Mean Absolute Error, MAE) и средняя абсолютная процентная ошибка (Mean Absolute Percentage Error, MAPE). Эти метрики позволяют объективно оценить точность и качество моделей, выявить наиболее подходящую из них и сделать обоснованные выводы о применимости различных методов машинного обучения [9].
Среднеквадратичная ошибка (MSE) измеряет среднее квадратичное отклонение предсказанных значений от фактических. Чем меньше значение MSE, тем точнее модель, так как это означает меньшую ошибку предсказания в среднем.
Коэффициент детерминации (R²) показывает, какая доля вариации зависимой переменной объясняется независимыми переменными модели. Значение R² варьируется от 0 до 1, где 1 означает, что модель идеально объясняет все вариации данных.
Средняя абсолютная ошибка (MAE) измеряет среднее абсолютное отклонение предсказанных значений от фактических. Это более интерпретируемая метрика, так как она выражается в тех же единицах, что и исходные данные, и позволяет понять, на сколько в среднем модель ошибается.
Средняя абсолютная процентная ошибка (MAPE) измеряет среднюю абсолютную процентную ошибку предсказаний и часто используется для интерпретации точности моделей в процентах, что удобно для сравнения моделей в разных контекстах.
Результаты исследования и их обсуждение
В рамках исследования для прогнозирования академической успеваемости студентов последовательно применялись три метода машинного обучения: линейная регрессия – как базовая модель для выявления линейных зависимостей, полиномиальная регрессия – для анализа нелинейных взаимосвязей и случайный лес – как ансамблевый алгоритм, способный эффективно обрабатывать сложные данные с высокой размерностью. Ниже представлены детализированные результаты, их интерпретация и обоснование выбора методов, подтверждающие ключевую роль современных алгоритмов в решении задач образовательной аналитики. Сравнительный анализ эффективности линейной, полиномиальной регрессии и случайного леса в прогнозировании академической успеваемости студентов проведен на основе ключевых метрик (MSE, R², MAE, MAPE). Основная задача – определить, насколько разные модели способны выявлять взаимосвязи между школьными оценками, экзаменационными результатами и экспертными оценками. Далее представлены детализированные результаты, интерпретация точности алгоритмов и обоснование выбора оптимального подхода.
Линейная регрессия – это базовая модель машинного обучения, используемая для задач регрессии. Она оценивает линейные зависимости между входными признаками и целевой переменной. Основная идея заключается в нахождении линейной зависимости, которая минимизирует сумму квадратов ошибок между предсказанными и фактическими значениями.
Математическое обоснование регрессии заключается в использовании метода наименьших квадратов для нахождения оптимальных коэффициентов линейной модели, минимизирующих сумму квадратов ошибок. Модель описывается уравнением
ŷ = β0 + β1x1 + β2x2 + … + βnxn , (2)
где ŷ – предсказанное значение, β0 – свободный член, β1, β2, …, βn – коэффициенты модели, x1, x2, …, xn – входные признаки.
Для достаточного качества модели были подобраны оптимальные гиперпараметры с использованием базового метода обучения, предоставляемого библиотекой scikit-learn [10]. Данная модель не требует значительной настройки параметров, так как использует стандартный метод наименьших квадратов. Оценки качества модели представлены в табл. 1.
Таблица 1
Оценки качества модели линейной регрессии
|
Метрика |
Prepod_mark |
VKR |
|
MSE |
178,2677 |
400,9954 |
|
R² |
0,6873 |
0,7280 |
|
MAE |
9,8820 |
15,0149 |
|
MAPE |
25,7830 |
– |
Основываясь на полученных значениях, можно сделать следующий вывод о качестве модели. Данная регрессия показала недостаточную точность предсказаний для обеих целевых переменных, что говорит о слабой применимости данной модели для решения такой задачи.
Полиномиальная регрессия – это расширение линейной регрессии, которое позволяет моделировать нелинейные зависимости путем добавления полиномиальных признаков. Основная идея заключается в трансформации исходных признаков в полиномиальные и применении линейной регрессии на новых признаках.
Математическое обоснование полиномиальной регрессии заключается в использовании метода наименьших квадратов для нахождения оптимальных коэффициентов полиномиальной модели, минимизирующих сумму квадратов ошибок. Модель описывается уравнением
ŷ = β0 + β1x + β2x2 + … + βnxn , (3)
где ŷ – предсказанное значение, β0 – свободный член, β1, β2, …, βn – коэффициенты модели, x1, x2, …, xn – исходные признаки, n – степень полинома.
Оценки качества модели представлены в таблице 2.
Таблица 2
Оценки качества модели полиномиальной регрессии
|
Метрика |
Prepod_mark |
VKR |
|
MSE |
75,5864 |
181,9152 |
|
R² |
0,8674 |
0,8766 |
|
MAE |
4,8756 |
7,6984 |
|
MAPE |
13,8591 |
– |
Основываясь на полученных значениях, можно сделать следующий вывод о качестве модели. Полиномиальная регрессия показала значительно лучшие результаты по сравнению с линейной регрессией для прогнозирования оценок преподавателей и ВКР студентов. Значительно более низкие значения MSE указывают на то, что модель делает меньшие ошибки в предсказаниях. Высокие значения R² подтверждают, что модель хорошо объясняет вариации данных. Более низкие значения MAE и MAPE для оценки преподавателей указывают на более точные предсказания.
Таким образом, полиномиальная регрессия лучше справляется с задачей прогнозирования академической успеваемости студентов, обеспечивая более точные и надежные результаты [11].
Случайный лес (Random Forest)– это ансамблевый метод машинного обучения, который использует множество деревьев решений для улучшения точности и устойчивости модели [12]. Метод случайного леса основан на идее создания множества деревьев решений с использованием случайных подвыборок данных и случайных подмножеств признаков. Прогноз конечной модели получается путем усреднения прогнозов всех деревьев.
Математическое обоснование случайного леса заключается в построении N деревьев решений, где каждое дерево обучается на случайной подвыборке данных с использованием случайного подмножества признаков. Итоговый прогноз для регрессии получается путем усреднения прогнозов всех деревьев:
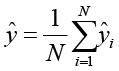 , (4)
, (4)
где ŷi – прогноз i-го дерева.
Случайный лес реализован с помощью библиотеки scikit-learn. Инструменты, использованные для реализации, включают Random Forest Regressor для построения модели случайного леса [13].
Оценки качества модели представлены в таблице 3.
Таблица 3
Оценки качества модели случайный лес
|
Метрика |
Prepod_mark |
VKR |
|
MSE |
22,7476 |
9,1656 |
|
R² |
0,9601 |
0,9938 |
|
MAE |
2,3277 |
1,1600 |
|
MAPE |
5,1938 |
– |
Основываясь на полученных значениях, можно сделать следующий вывод о качестве модели. Случайный лес показал лучший результат среди выбранных моделей для прогнозирования академической успеваемости студентов [14, 15]. Значительно более низкие значения MSE и высокие значения R² указывают на то, что модель случайного леса способна эффективно объяснять вариации данных и делать точные прогнозы. Значения MAE также подтверждают высокую точность модели, а низкий MAPE для оценки Prepod_mark указывает на малую среднюю абсолютную процентную ошибку.
Итоговое сравнение моделей приведено в табл. 4.
Таблица 4
Сравнение значимых оценок исследуемых моделей
|
Модель |
Prepod_mark (MSE) |
Prepod_mark (R²) |
VKR (MSE) |
VKR (R²) |
|
Линейная регрессия |
178,27 |
0,6873 |
401,00 |
0,7280 |
|
Полиномиальная регрессия |
75,59 |
0,8674 |
181,92 |
0,8766 |
|
Случайный лес |
22,75 |
0,9601 |
9,17 |
0,9938 |
Заключение
Проведенное исследование подтвердило, что применение алгоритмов машинного обучения, в частности случайного леса, позволяет существенно повысить точность прогнозирования успеваемости студентов за счет учета нелинейных зависимостей в данных. Линейная регрессия, несмотря на простоту интерпретации, показала ограниченную эффективность, а полиномиальная модель может давать результаты достаточной точности, но при этом требует дополнительной настройки для минимизации риска переобучения.
Полученные результаты работы показывают, что благодаря применению современных методов машинной обработки статистических данных возможно проведение прогнозирования будущей успеваемости студента в вузе еще на этапе его поступления в вуз на выбранное направление обучения, располагая только данными школьных оценок об успеваемости. Отдельно можно отметить, что использование только «объективных» данных о школьной успеваемости, без учета «субъективных» факторов, таких как мотивация обучающегося, взаимодействие с учителем, интерес к школьному предмету и т.д., также может показывать неплохие результаты прогнозирования. Однако авторы работы считают, что внедрение некоторого количества «субъективных» факторов в качестве исходных данных прогнозирования может помочь еще больше повысить качество прогнозирования успеваемости, в связи с чем планируется продолжать дальнейшие исследования в данной области.
Практическая значимость работы видится в создании автоматизированных систем самостоятельного прогнозирования возможной будущей успеваемости абитуриентов в вузе для выбранных направлений обучения. Применение таких систем поможет абитуриентам снизить риск неудачного выбора будущего направления обучения, а следовательно, повысить его возможную компетентность на рынке труда в будущем.
Конфликт интересов
Библиографическая ссылка
Ромащенко А.И., Щербин С.И., Харитонов И.М., Панфилов А.Э., Жаравин Н.С. ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ МАШИННОГО ОБУЧЕНИЯ ДЛЯ ПРОГНОЗИРОВАНИЯ БУДУЩЕЙ УСПЕВАЕМОСТИ АБИТУРИЕНТОВ В ВУЗЕ // Современные наукоемкие технологии. 2025. № 9. С. 132-136;URL: https://top-technologies.ru/ru/article/view?id=40497 (дата обращения: 01.03.2026).
DOI: https://doi.org/10.17513/snt.40497



