Введение
Обобщенное уравнение Бюргерса является сложным с точки зрения численного моделирования. В отличие от классического уравнения Бюргерса, обобщенное одновременно отражает затухание волнового поля, его деформацию под влиянием дисперсионных эффектов и воздействие внешних силовых полей и позволяет описывать акустические, гидродинамические и плазменные системы, где взаимодействие нескольких механизмов формирует широкий спектр динамических явлений [1; 2]. В реакционно-диффузионных и теплопередающих процессах обобщенное уравнение Бюргерса помогает прогнозировать распространение тепла и химических реагентов с учетом нелинейных реакций и градиентов концентрации [3, с. 146]. В аэрогазодинамике оно широко используется для изучения формирования и эволюции ударных волн, а также пограничных слоев в потоках с изменяющейся вязкостью [4]. В области плазменной физики модель позволяет исследовать турбулентные структуры и перенос заряда в магнитогидродинамических системах [5]. Микрофлюидные приложения требуют точного описания переноса микро- и наночастиц в средах со сложной реологией, что также реализуется с помощью обобщенного уравнения Бюргерса [6]. В экологии и эпидемиологии данная постановка служит для моделирования миграции популяций и распространения инфекционных агентов в неоднородных средах [7]. Астрономы применяют эту модель для изучения медленно распространяющихся волн в корональных магнитных петлях Солнца, где вязкость убывает экспоненциально, а внешние магнитные поля диктуют поведение плазмы [8; 9].
Классическое уравнение Бюргерса с постоянным коэффициентом вязкости и без источников допускает аналитическое решение через преобразование Коула – Хопфа (Cole-Hopf transform), которое сводит нелинейное уравнение к линейному уравнению теплопроводности, а также допускает применение классических аналитических методов – преобразования Лапласа и Фурье, метод обратных задач и асимптотические разложения ограничены применимостью к линейным или сильно упрощенным ситуациям. В отличие от классического уравнения Бюргерса, его обобщенная формулировка включает коэффициент диффузии как функцию времени, линейный источниковый член, а также кусочно-заданные начальные и жесткие граничные условия. Для таких задач аналитическое решение в общем виде не существует. Возможно применение асимптотических и приближенных методов решения уравнения Бюргерса при малых или больших значениях параметров, построенных с помощью разложений, многомасштабного анализа. При фиксированных параметрах и существенных упрощениях, приводящих к частным случаям, можно получить частичные аналитические решения. В большинстве реальных краевых задач с переменными коэффициентами и резкими фронтами аналитика уступает место высокоэффективным численным методикам, способным сочетать точность и устойчивость при обработке сложных неразрывностей. За последнее десятилетие разработаны и усовершенствованы несколько ключевых подходов:
− Высокопорядковые WENO-схемы конечных разностей, которые предотвращают искусственные колебания при прорисовке резких фронтов и сохраняют физические границы решения [1; 2]. Временная дискретизация – неявно-явные (IMEX) Runge – Kutta методы 3–4-го порядка (для конвекции явный шаг, для диссипации – неявный).
− Современные BSQI-WENO-подходы с полунепрерывной адаптацией предлагают исследователям интеллектуальное решение для численного моделирования: алгоритм самостоятельно выбирает сплайновую квазинтерполяцию для регулярных зон и переходит к WENO-восстановлению пятого порядка при обнаружении резких переходов. Временная составляющая обеспечивается методикой Рунге – Кутты четвертой степени точности с адаптивным контролем погрешности, базирующимся на интегральном осреднении локальных невязок [4].
− Гибридные методы конечных элементов и конечных разностей (FEM-FDM) обеспечивают оптимальный баланс между точностью аппроксимации диффузионных членов и простотой реализации конвективных слагаемых [5]. В рамках данного подхода конечные элементы применяются для дискретизации вторых производных (диффузионный член), конечные разности используются для нелинейного конвективного члена, а источниковые слагаемые аппроксимируются локальными методами.
− Среди различных численных методов, применяемых для решения уравнения Бюргерса, особого внимания заслуживают методы, основанные на квадратичных B-сплайнах и конечных элементах, которые демонстрируют хорошую сходимость и устойчивость [10].
− Двухэтапные Lax – Wendroff схемы четвертого порядка (двухэтапные схемы RK4-WENO5 и GRP4-HWENO5), демонстрирующие высокую временную и пространственную точность при умеренных ресурсных затратах [6]. На первом этапе осуществляется расчет промежуточных значений, а на втором – коррекция на базе локальной задачей Римана, при этом экономия памяти достигается за счет одноуровневой организации шагов.
− Специальные WENO-методы для неравномерных сеток, сохраняющие формальный порядок аппроксимации даже на сильно искаженных разрежениях сетки [7]. В данном случае используются простые индикаторы гладкости с линейной стоимостью по порядку, а сам алгоритм автоматически адаптирует веса при локальных сжатиях/растяжениях ячеек.
− Имплицитно-эксплицитные Runge – Kutta схемы (IMEX), которые обеспечивают устойчивость при жесткости уравнения, не теряя эффективности явных шагов по конвекции [9; 11].
− Дискретизации discontinuous Galerkin с локальной адаптацией порядка полиномов и гибкой сеточной структурой для сложных геометрий [5].
− Спектральные и спектрально-элементные методы (spectral/hp), гарантирующие экстремально высокую точность при моделировании дисперсионных эффектов и гладких решений [11].
− Среди различных численных методов, применяемых для решения уравнения Бюргерса, особого внимания заслуживают методы, основанные на квадратичных B-сплайнах и конечных элементах, которые демонстрируют хорошую сходимость и устойчивость [12; 13].
− Современные итерационные методы, такие как ускоренный новый итерационный метод (ARNIM) и модифицированный New Iterative Method (MNIM), которые демонстрируют высокую скорость сходимости и эффективность при решении нелинейных уравнений типа Бюргерса – Хаксли без необходимости дискретизации [14; 15].
Каждый из перечисленных подходов обладает своим балансом между устойчивостью, сходимостью и вычислительными затратами для частных случаев обобщенного уравнения Бюргерса. Целью данной работы является сравнительный анализ современных численных методов решения обобщенного уравнения Бюргерса с нелинейной конвекцией, переменной диссипацией и линейным источниковым членом. Исследование направлено на оценку точности, устойчивости и вычислительной эффективности рассматриваемых методов при моделировании нелинейных волновых процессов.
Материалы и методы исследования
В данной работе рассматривается обобщенное уравнение Бюргерса, описывающее эволюцию поля U(y,τ) с нелинейной конвекцией 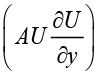 , диффузией
, диффузией 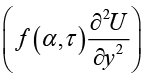 и потенциальным (BαU) членами на пространственном интервале с граничными условиями Дирихле и заданным начальным распределением U(y,0). В качестве математической модели использовано уравнение
и потенциальным (BαU) членами на пространственном интервале с граничными условиями Дирихле и заданным начальным распределением U(y,0). В качестве математической модели использовано уравнение
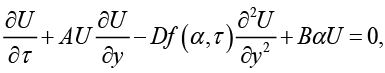 (1)
(1)
где параметры A, В, α и D задают интенсивность нелинейного, диссипативного и потенциального вкладов, а функция f(α,τ) задает нелинейные и диффузионные свойства системы.
Рассматриваемое обобщенное уравнение (1) сохраняет нелинейный конвективный член 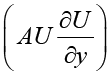 , аналогичный классическому уравнению Бюргерса, однако коэффициент A фиксирован и отличается от единицы. Диффузионный член содержит коэффициент Df(α,τ) = De–ατ, который экспоненциально убывает (D > 0) или экспоненциально возрастает (D < 0) по времени при положительных значениях α, что приводит к переменной жесткости задачи. Линейный член BαU вносит дополнительное затухание или источник, влияя на динамику решения.
, аналогичный классическому уравнению Бюргерса, однако коэффициент A фиксирован и отличается от единицы. Диффузионный член содержит коэффициент Df(α,τ) = De–ατ, который экспоненциально убывает (D > 0) или экспоненциально возрастает (D < 0) по времени при положительных значениях α, что приводит к переменной жесткости задачи. Линейный член BαU вносит дополнительное затухание или источник, влияя на динамику решения.
Явный метод Эйлера с центральными разностями и адаптивным шагом. Для аппроксимации уравнения можно использовать явный метод Эйлера, в котором временная производная аппроксимируется разностным отношением первого порядка (2), а пространственные производные – центральными разностями второго порядка (3). Обновление решения на временном шаге n+1 имеет вид (4)
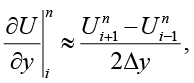 (2)
(2)
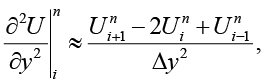 (3)
(3)
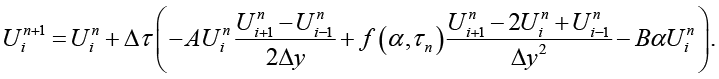 (4)
(4)
Схема (4) обладает первым порядком точности по времени и вторым порядком по пространству. Данный метод прост в реализации и позволяет быстро получить приближенное решение. Однако метод является условно устойчивым и требует ограничения на шаг по времени, связанного с условием Куранта – Фридрихса – Леви (CFL), которое в данном случае зависит от максимального значения нелинейного члена 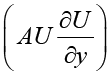 , переменного диффузионного коэффициента (f(α,τ)) и линейного источника (Bα). Наличие разрывов в начальном условии и переменного коэффициента f(α,τ) может приводить к появлению численных осцилляций и артефактов, особенно при больших значениях параметров α и больших R, что требует дополнительного сглаживания или использования схем с ограничителями. Например, при экспоненциально убывающей функции (Df(α,τ) = De–ατ) устойчивость схемы становится зависимой от времени. При уменьшении f(α,τ) диффузионное сглаживание ослабевает, и ограничение на шаг по времени становится более жестким из-за усиления конвективного и нелинейного влияния. Линейный источник может выступать как затухание (при Bα > 0) или как источник энергии (при отрицательных значениях). Это влияет на поведение решения и может усиливать или ослаблять устойчивость численной схемы. В частности, шаг по времени должен удовлетворять неравенству (5).
, переменного диффузионного коэффициента (f(α,τ)) и линейного источника (Bα). Наличие разрывов в начальном условии и переменного коэффициента f(α,τ) может приводить к появлению численных осцилляций и артефактов, особенно при больших значениях параметров α и больших R, что требует дополнительного сглаживания или использования схем с ограничителями. Например, при экспоненциально убывающей функции (Df(α,τ) = De–ατ) устойчивость схемы становится зависимой от времени. При уменьшении f(α,τ) диффузионное сглаживание ослабевает, и ограничение на шаг по времени становится более жестким из-за усиления конвективного и нелинейного влияния. Линейный источник может выступать как затухание (при Bα > 0) или как источник энергии (при отрицательных значениях). Это влияет на поведение решения и может усиливать или ослаблять устойчивость численной схемы. В частности, шаг по времени должен удовлетворять неравенству (5).
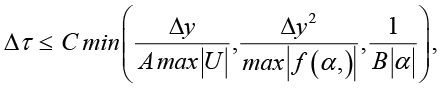 (5)
(5)
где C – константа порядка единицы. При нарушении этого условия численное решение становится неустойчивым и может демонстрировать неограниченный рост ошибок. Следовательно, для обеспечения устойчивости схемы (4) требуется достаточно мелкий шаг по времени с динамическим контролем.
Полунеявный метод Кранка – Николсон с адаптивным шагом. Для повышения устойчивости и точности для численного решения обобщенного уравнения Бюргерса применим полунеявный метод Кранка – Николсон, в котором диффузионный член с переменным коэффициентом аппроксимируется неявно, а нелинейный конвективный и линейный члены – явно, а при необходимости можно использовать итерационные процедуры. Для рассматриваемой задачи схема имеет вид
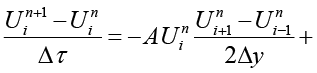
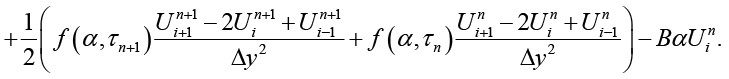 (6)
(6)
Схема (4) обладает вторым порядком точности по времени для диффузионного члена и улучшенной устойчивостью, что позволяет использовать более крупные шаги по времени по сравнению с явными методами. Решение на каждом временном шаге требует решения системы линейных уравнений, что увеличивает вычислительную сложность, но обеспечивает стабильность и точность при жестких параметрах. Минимальный шаг Δy определяется требованиями точности и особенностями решения (например, шириной фронтов, характером переходов), а при слишком крупном шаге Δy возникают численные диффузия и потеря точности, а также возможны нестабильности, связанные с аппроксимацией производных. Аппроксимация диффузионного члена неявно в полунеявном методе Кранка – Николсон значительно улучшает устойчивость по сравнению с явными методами, но требуются ограничения на Δτ. Для удобства записи введем обозначения
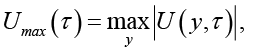
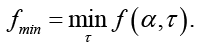
Тогда для обеспечения численной устойчивости и точности полунеявного метода Кранка – Николсон необходимо, чтобы временной шаг Δτ удовлетворял следующему условию
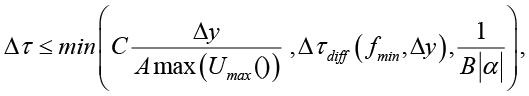 (7)
(7)
где C ∈ (0,1].
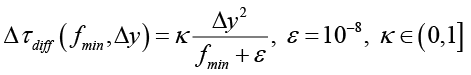 .
.
Выбор κ = 0,5 – это компромисс между эффективностью и устойчивостью. При наблюдении численных осцилляций или расходимости следует уменьшить κ до 0,3, а если решение стабильно и хочется увеличить шаг по времени, то значение κ можно увеличить до 0,8–1,0.
Неявные схемы с использованием метода Ньютона для решения нелинейной системы. В решении обобщенного уравнения Бюргерса (1) при применении полностью неявной схемы можно использовать такой итерационный численный метод для нахождения корней нелинейной системы, как метод Ньютона. Для получения конечно-разностного представления уравнения (1) используем неявную схему Эйлера по времени:
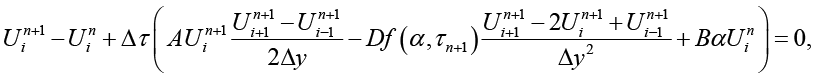 (8)
(8)
где 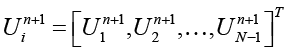 – вектор неизвестных на новом временном слое (граничные значения
– вектор неизвестных на новом временном слое (граничные значения 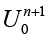 и
и 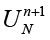 задаются жестко). В результате получаем систему вида
задаются жестко). В результате получаем систему вида 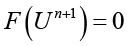 , которую решаем методом Ньютона (9).
, которую решаем методом Ньютона (9).
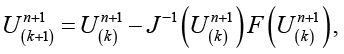 (9)
(9)
где 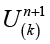 – приближение решения на итерации (k),
– приближение решения на итерации (k),
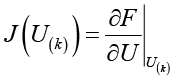 – якобиан системы,
– якобиан системы,
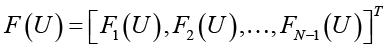 .
.
Элементы якобиана для каждого узла 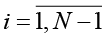 и переменной
и переменной 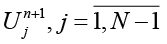 определяются
определяются 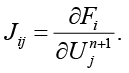
Учитывая, что Fi зависит только от 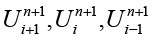 получаем разреженную структуру якобиана с элементами:
получаем разреженную структуру якобиана с элементами:
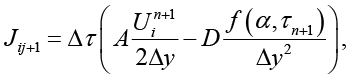
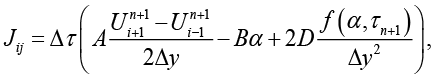
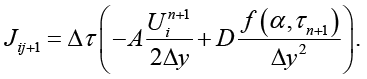 (10)
(10)
Метод Ньютона обладает квадратичной сходимостью, но только при достаточно близком начальном приближении и требует вычисления якобиана, что существенно увеличивает вычислительные затраты. Для повышения устойчивости предпочтительнее использовать модифицированный метод Ньютона или методы с линейным поиском. В задачах с жесткими нелинейностями и резкими переходами требуется дополнительное регуляризующее сглаживание или адаптивный выбор параметров. Данный метод является мощным инструментом для решения нелинейных систем, возникающих при неявной дискретизации уравнения Бюргерса.
Метод линий с центральными разностями и жестким адаптивным временным интегратором является классическим и широко применяемым подходом для решения нелинейных жестких уравнений в частных производных [12; 13]. В данной работе используется пространственная дискретизация с помощью центральных разностей второго порядка точности для аппроксимации производных (2) и (3), а для интегрирования по времени применяется жесткий адаптивный решатель обыкновенных дифференциальных уравнений, основанный на методах обратных разностных формул (Backward Differentiation Formula). Следует отметить, что центральные разности для диффузионного члена условно устойчивы при явных схемах, однако в рассматриваемом методе временная интеграция выполняется отдельно, и устойчивость решения определяется выбранным временным интегратором. Центральные разности для нелинейного конвективного члена не являются монотонными и могут приводить к численным осцилляциям, особенно при наличии резких градиентов или разрывов.
Результаты исследования и их обсуждение
Во всех численных экспериментах для решения уравнения (1) с заданными начальными и граничными условиями используется равномерная или локально адаптивная пространственная сетка (h-адаптация) с минимальным размером ячейки ∆x, обеспечивающим адекватное разрешение областей резких градиентов. Временной шаг ∆τ подчиняется критерию CFL для явных конвективных методов и контролю локальной ошибки для IMEX-схем. Для оценки качества решений и сравнения методов использованы e1, e2 и e∞ – нормы ошибки относительно эталонного решения на очень мелкой сетке, время вычисления и шаг по пространству. Для тестирования алгоритмов выбран частный случай уравнения Бюргерса с известным аналитическим решением. В уравнении (1) выбраны значения коэффициентов A = 1, B = 0, и f(α,τ) = v = Const > 0, D = 1, что приводит к классическому уравнению Бюргерса (11) с однородными граничными условиями и начальным состоянием (12). Наличие потенциального члена приводит к изменению амплитуды решения в соответствии с видом задаваемой функции.
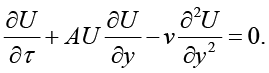 (11)
(11)
U(0,τ) = 0, U(1,τ) = 0 при τ > 0 и
U(y,0) = sin(πy) при 0 < y < 1. (12)
Точное решение для данной задачи представлено в работе [10; 13] и имеет вид
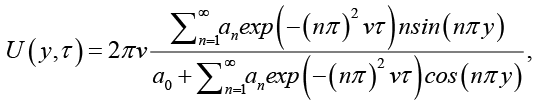
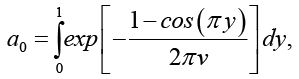
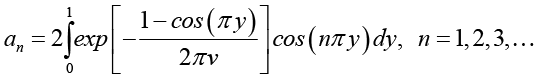 (13)
(13)
В табл. 1 приведены результаты численного моделирования задачи (11) с граничными условиями нулевого значения на границах по пространственной переменной и начальным условием в виде синусоиды (12). Исследование проведено для трех значений параметра вязкости v: 0,1; 0,5 и 1,5, с использованием четырех численных методов – явного метода Эйлера с адаптивным шагом, метода Кранка – Николсон с адаптивным шагом, неявных схем с методом Ньютона (три итерации) и метода линий. Для каждого метода представлены относительные нормы ошибки (14)–(16), минимальный шаг по времени (Δtmin) и среднее время вычисления одного шага по времени (τcp). Явный метод Эйлера демонстрирует наибольшие значения ошибок при всех рассматриваемых уровнях вязкости, а также требует существенно меньших временных шагов из-за ограничений по устойчивости, что снижает его точность, но его простой алгоритм не требует итерационных процедур и поэтому обладает минимальным временем вычислений. Метод Кранка – Николсон с адаптивным шагом и метод линий показывают значительно более высокую точность и более крупные временные шаги без потери устойчивости, при этом время их работы остается приемлемым. Неявные схемы в сочетании с методом Ньютона занимают промежуточное положение: они обеспечивают меньшую точность по сравнению с Кранком – Николсон и методом линий, но требуют большего времени из-за сложности алгоритма и необходимости итеративных вычислений. При увеличении параметра вязкости наблюдается рост ошибок у явного метода Эйлера, тогда как методы Кранка – Николсон и линий сохраняют стабильные и низкие значения ошибок, что подчеркивает их надежность и эффективность при моделировании процессов с выраженным диффузионным характером. Временные затраты у всех методов, кроме явного, остаются относительно постоянными, что свидетельствует о хорошей адаптивности и сбалансированности выбранных численных схем.
На рисунке показаны результаты численного решения задачи (11)–(12) методом линий с центральными разностями и жестким адаптивным временным интегратором. Аналогичный результат дают остальные методы.
Таблица 1
Результаты по нормам ошибок при заданном значении шага по координате при dy = 2.040816e-02, шаг по времени и среднее время выполнения одного шага
|
Методы |
e1 |
e2 |
e∞ |
Δτmin |
τcp, сек |
|
v = 0.1 |
|||||
|
Явный метод Эйлера |
8.395e-02 |
9.951e-02 |
1.675e-01 |
1.6733e-04 |
0.000090 |
|
Метод Кранка – Николсон с адаптивным шагом |
4.457e-03 |
5.440e-03 |
9.113e-03 |
2.0408e-03 |
0.000094 |
|
Неявные схемы с методом Ньютона (итераций 3) |
4.589e-03 |
5.440e-03 |
9.082e-03 |
2.0408e-03 |
0.000208 |
|
Метод линий |
4.599e-03 |
5.539e-03 |
9.109e-03 |
2.0408e-03 |
0.000335 |
|
v = 0.5 |
|||||
|
Явный метод Эйлера |
2.390e-01 |
2.672e-01 |
3.839e-01 |
6.7071e-05 |
0.000003 |
|
Метод Кранка – Николсон с адаптивным шагом |
2.620e-03 |
3.000e-03 |
4.542e-03 |
2.0408e-03 |
0.000044 |
|
Неявные схемы с методом Ньютона (итераций 3) |
3.603e-03 |
4.045e-03 |
5.877e-03 |
2.0408e-03 |
0.000112 |
|
Метод линий |
2.666e-03 |
3.029e-03 |
4.523e-03 |
2.0408e-03 |
0.000109 |
|
v = 1.5 |
|||||
|
Явный метод Эйлера |
4.803e-01 |
5.337e-01 |
7.544e-01 |
2.4967e-05 |
0.000004 |
|
Метод Кранка – Николсон с адаптивным шагом |
7.039e-04 |
7.856e-04 |
9.113e-03 |
2.0408e-03 |
0.000041 |
|
Неявные схемы с методом Ньютона |
3.925e-03 |
4.363e-03 |
6.181e-03 |
2.0408e-03 |
0.000107 |
|
Метод линий |
7.282e-04 |
8.114e-04 |
1.156e-03 |
2.0408e-03 |
0.000070 |
Источник: составлено автором на основе полученных данных в ходе исследования.
Таблица 2
Сравнение метода Кранка – Николсон и метода линий с центральными разностями и адаптивным жестким интегратором для обобщенного уравнения Бюргерса
|
A |
D |
B |
τKN, сек |
ΔτKN |
τL, сек |
ΔτL |
|
0,50 |
0,05 |
-0,10 |
0,128103 |
0,000342 |
0,011092 |
0,005025 |
|
0,50 |
0,05 |
0,10 |
0,115607 |
0,000342 |
0,008708 |
0,005025 |
|
0,50 |
0,50 |
-0,10 |
1,111318 |
0,000002 |
0,011125 |
0,005025 |
|
0,50 |
0,50 |
0,10 |
1,149861 |
0,000002 |
0,010020 |
0,005025 |
|
0,50 |
1,00 |
-0,10 |
2,214532 |
0,000046 |
0,011786 |
0,005025 |
|
0,50 |
1,00 |
0,10 |
2,207285 |
0,000046 |
0,011699 |
0,005025 |
|
1,00 |
0,05 |
-0,10 |
0,092808 |
0,000918 |
0,009693 |
0,005025 |
|
1,00 |
0,05 |
0,10 |
0,089061 |
0,000918 |
0,009338 |
0,005025 |
|
1,00 |
0,50 |
-0,10 |
0,899959 |
0,000073 |
0,012594 |
0,005025 |
|
1,00 |
0,50 |
0,10 |
0,904544 |
0,000073 |
0,013889 |
0,005025 |
|
1,00 |
1,00 |
-0,10 |
1,825258 |
0,000011 |
0,014695 |
0,005025 |
|
1,00 |
1,00 |
0,10 |
1,839204 |
0,000011 |
0,016778 |
0,005025 |
Источник: составлено автором на основе полученных данных в ходе исследования.
В табл. 2 представлены результаты численного решения обобщенного уравнения Бюргерса с применением методов Кранка – Николсон и линий, включая параметры A, D, B, а также время вычислений и величину временного шага. Из табл. 2 видно, что при фиксированном значении A и постоянном знаке B увеличение диффузионного коэффициента D приводит к значительному росту времени вычислений и уменьшению временного шага у метода Кранка – Николсон, что связано с необходимостью более точной дискретизации для сохранения устойчивости.
а) 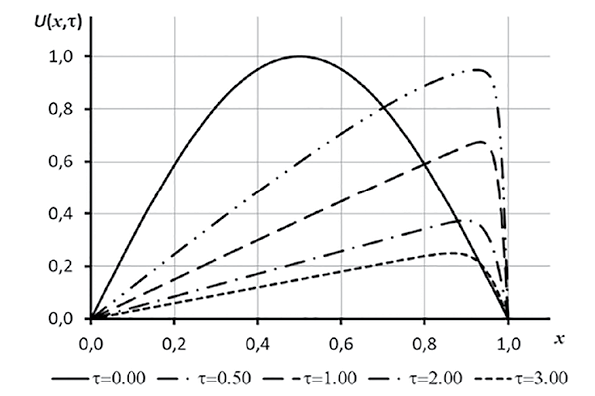
b) 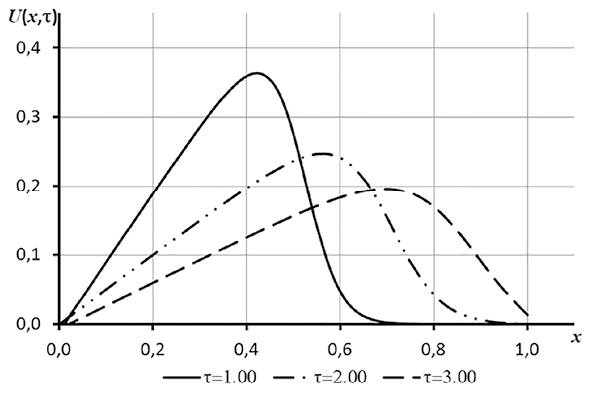
Численное решение уравнения Бюргерса для различных моментов времени Источник: составлено автором по результатам данного исследования
Как видно из результатов численного моделирования, метод линий показывает высокую эффективность и устойчивость к изменению параметров и имеет относительно низкое время работы с неизменным шагом по времени. Изменение знака параметра B с +0,1 на -0,1 слабо влияет на производительность обоих методов, а повышение значения A с 0,5 до 1 и увеличение значений параметра D c 0,05 до 1 способствует увеличению времени вычислений у метода Кранка – Николсон, при этом метод линий более стабилен и экономичен в вычислительном плане, что делает его более предпочтительным для решения обобщенного уравнения Бюргерса.
Заключение
В данной статье проведен комплексный анализ таких современных численных методов, как метод линий с жестким адаптивным интегратором, полунеявный метод Кранка – Николсон, метод Эйлера и неявные схемы с использованием метода Ньютона для решения обобщенного уравнения Бюргерса с нелинейной конвекцией, переменной диссипацией и потенциальным членом. Анализ полученных результатов показал, что такие методы, как Кранка – Николсон и метод линий, обеспечивают оптимальное сочетание точности, устойчивости и вычислительной эффективности при решении задач с переменными коэффициентами и резкими фронтами. Явный метод Эйлера более прост в реализации, но имеет более низкую точность и ограниченную устойчивость при увеличении параметра вязкости. Неявные схемы с методом Ньютона имеют высокую точность, но при этом требовательны к вычислительным ресурсам, что снижает их эффективность в сравнении с альтернативными методами. При этом метод линий имеет высокую устойчивость к изменению параметров задачи и сохраняет стабильное время вычислений, что делает его предпочтительным для практического применения в моделировании нелинейных волн.
Дальнейшие исследования могут быть направлены на несколько ключевых областей. Во-первых, расширение класса решаемых задач и учет дополнительных физических эффектов, включая аэродинамические воздействия и многомерность. Во-вторых, разработка более совершенных адаптивных алгоритмов. В-третьих, создание гибридных численных методов, объединяющих преимущества различных подходов для повышения общей эффективности вычислений.
Конфликт интересов
Библиографическая ссылка
Катаева Л.Ю. АНАЛИЗ ЧИСЛЕННЫХ МЕТОДОВ РЕШЕНИЯ ОБОБЩЕННОГО УРАВНЕНИЯ БЮРГЕРСА ДЛЯ НЕЛИНЕЙНЫХ ВОЛН // Современные наукоемкие технологии. 2025. № 9. С. 78-86;URL: https://top-technologies.ru/ru/article/view?id=40489 (дата обращения: 01.03.2026).
DOI: https://doi.org/10.17513/snt.40489



