Введение
Для реализации математического описания реальных объектов применяется агентный подход. Под агентом в математическом моделировании понимается некоторая сущность (человек, машина, животное, город и др.), находящаяся и действующая в определенной внешней среде. Выделяют несколько типов поведения агентов: взаимодействие с другими агентами или нейтралитет – приобретенное знание агента, основанное на его опыте взаимодействия и преследуемых целях [1]. Иначе говоря, под агентом понимается элемент модели, который может иметь поведение, память (историю), контакты и т.д.
Автоматом называется абстрактное устройство, которое выполняет определенные операции без вмешательства человека. Автоматы, имеющие конечное число состояний, называются конечными. Такой тип является наиболее распространенным в математическом моделировании. Любые автоматы, в том числе конечные, включают в себя состояния и переходы. При поступлении на автомат чего-либо (например, символа) он совершает переход в другое состояние, что регулируется его функцией перехода, которая принимает в качестве аргументов предыдущее состояние и текущий введенный символ.
В научных изданиях [2–4] рассматривается использование гибридного автомата как частного случая конечного. Гибридные автоматы отличаются сочетанием двух видов состояний – непрерывных и дискретных. В узлы гибридного автомата интегрируются динамические системы, а смена поведения описывается дугами.
В общепринятом определении, используемом в том числе авторами [2–4], гибридным автоматом (ГА) называется совокупность
,
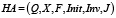где
− 
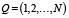– множество дискретных состояний автомата;
− 
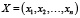– совокупность непрерывных переменных;
− 
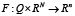– непрерывное поведение автомата;
− 
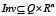– множество, на котором ГА не изменяет дискретное состояние;
− 
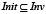– множество начальных значений ГА.
− 
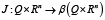– условие изменения дискретного состояния (рис. 1).
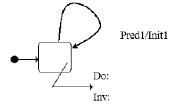
Рис. 1. Гибридный автомат Источник: составлено автором на основе [2–4]
На рис. 1 выделены несколько ключевых компонентов: прямоугольник обозначает длительные процессы, стрелка с условиями и функцией инициализации указывает на остановку интегрирования и выбор новых начальных условий, а ломаная линия представляет интегрируемую систему и функцию-инвариант, определяющую свойства решения. Маленькая стрелка обозначает начальное состояние, которое выделяется, если в автомате присутствует несколько состояний.
В работах Б.И. Клебанова, Т.В. Антропова и Е. Рябкиной рассматривается возможность применения модели гибридного автомата для описания процессов поведения и развития агентов, обладающих определенными наборами потребностей, ресурсов и средств их реализации в заданной среде [5–7]. Поведение индивидуумов, в данном случае абитуриентов, определяется их потребностями, которые реализуются через типовые сценарии поведения (паттерны). Модель агента представлена в виде расширенного гибридного автомата, учитывающего альтернативы реализации потребностей и функции выбора при переходе автомата между состояниями.
Таким образом, формальная задача, решаемая с помощью математического моделирования на основе гибридного автомата, может быть четко изложена в терминах, применяемых как в дополнительном, так и в общем образовании.
Цель исследования – математическое описание процесса отбора обучающихся на программу дополнительного образования.
Материалы и методы исследования
Гибридные автоматы, сочетающие дискретные и непрерывные динамические процессы, находят применение в управлении сложными системами, включая образовательные. Хотя в рассмотренных работах прямое использование гибридных автоматов в педагогике не описано, ряд исследований предлагает методы, которые могут быть адаптированы для этой сферы.
В частности, исследования Клебанова и Антропова [4, 6] демонстрируют применение гибридных автоматов для формализации поведения агентов, что может быть использовано при проектировании адаптивных обучающих систем. Исследователи также предлагают гибридные модели на основе клеточных автоматов, которые потенциально применимы для персонализации образовательных траекторий и управления учебными процессами.
Косвенное отношение к теме имеют исследования, связанные с агентным моделированием, прогнозированием сложных систем и сетевым планированием [7, 8]. Эти работы предлагают методы, которые могут быть интегрированы в образовательные системы с использованием гибридных автоматов – например, для анализа успеваемости, автоматизации управления ресурсами или адаптации учебных программ. Таким образом, несмотря на отсутствие прямых примеров применения гибридных автоматов в образовании, рассмотренные исследования формируют теоретическую и методологическую основу для их внедрения в этой области.
Исследование проводилось в течение пяти лет (с сентября 2020 г. по июнь 2024 г.) среди абитуриентов-школьников, 13–17 лет, поступающих на программу образовательного проекта Яндекс.Лицей «Основы программирования на языке Python». При проведении исследования применялись следующие методы: наблюдение во взаимодействии с абитуриентом (интервьюирование, оценка мотивации к обучению), анализ данных (полученных выпускниками баллов при окончании обучения), проведение эксперимента (описание гибридного автомата, проверка его работоспособности на результатах поступающих) [8, 9].
Результаты исследования и их обсуждение
Центр дополнительного образования детей «Дом научной коллаборации имени М.В. Ломоносова» был создан при ФГАОУ ВО «Северный (Арктический) федеральный университет имени М.В. Ломоносова» в 2020 г. Основная деятельность центра связана с реализацией программ дополнительного образования для детей 5–11 классов.
В настоящее время реализуется более 40 программ для 60 групп обучающихся. За один учебный год через программы центра проходит около 1200 школьников Архангельска и области.
В связи с тем, что деятельность центра полностью финансируется Правительством Архангельской области, все занятия, расходные материалы, оборудование и пр. предоставляются обучающимся бесплатно, поэтому на все программы центра «Дом научной коллаборации имени М.В. Ломоносова» проводятся конкурсные испытания, чтобы зачислить в группы ребят, имеющих высокие способности к обучению. Получается, что из 4500 поданных заявлений на обучение зачисляется только 2000. Увеличить число обучающихся центр не имеет возможность, так как программы реализуются в лабораториях, в том числе университета, а их площадь и ресурсы ограничены.
Формирование рейтинга обучающихся производится по результатам вступительных испытаний с учетом мест, которые занимают дети, прошедшие на программу без дополнительного отбора. Если абитуриент не попал в группу, он заносится в условный резерв, ниже объясним назначение этого списка [10, 11].
Справляться с объемами поступающих документов сложно, иногда случаются ошибки. Чтобы учесть все данные, предлагается описание системы при помощи математического моделирования, в частности агентного моделирования, где ресурсом выступают знания, получаемые на занятиях, а агентами – абитуриенты и обучающиеся центра.
Рассматривать предлагается модель агента, имеющего одну потребность: получение ресурса, то есть новых знаний [12]. Определим, что целью описываемого агента, то есть абитуриента, подавшего документы, является получение знаний в неограниченном количестве. На практике это и наблюдается: несмотря на наличие программы курса, по которой работают педагоги, она может быть расширена и усложнена при соответствующем «запросе» от обучающихся.
Обозначим множество состояний агента: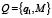 
, где q1 – состояние покоя, М – допустимое множество способов получения знаний.
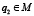– при выборе определенного способа получения знаний агент начинает их приобретать.
Также стоит ввести функцию
,
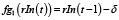где rIn – внутренний параметр ресурса агента, δ – величина, на которую изменяется за один год (такт) значение rIn. Это функция уменьшения контролируемого внутреннего параметра агента с течением времени в состоянии q1, то есть увеличение уровня знаний ученика.
fv1 – функция выбора способа получения необходимых новых знаний.
fe1 – функция увеличения объема знаний ребенка (с промежуточной и итоговой аттестациями) при реализации выбранного способа получения компетенций в состоянии q2.
Тогда
,
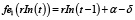где α – величина приращения показателя rIn, то есть повышение уровня знаний.
Стоит заметить, что уровень знаний у детей может быть разным, то есть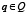 
;
E – множество дуг переходов между двумя состояниями. Так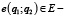 
дуга между q1 и q2;
P{p1} – множество потребностей, но в рассматриваемом в статье случае она единственная – p1.
Введем также величину rInT – такой критический уровень знаний ребенка, при котором возникает потребность их увеличения.
Множество возможных событий можно определить следующим образом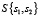 
, где 
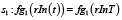– событие, при котором возникает потребность p1, то есть получения новых знаний;
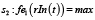– потребность в получении новых знаний удовлетворена (программа освоена, выдан сертификат об окончании обучения),
G – множество условий переходов между состояниями q1 и q2. Тогда
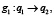если произошло событие s1;
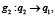если произошло событие s2.
Такая модель может реализовываться ежегодно, так как любая программа рассчитана на один учебный год, следовательно, в новом учебном году можно выбрать другое направление обучения, что повышает уровень имеющихся знаний у ребенка. Также при использовании такого рода моделирования становится понятно, каких детей необходимо принимать на обучение в первую очередь.
Представим работу автомата в виде графика, отображающего результаты освоения 44 выпускниками программ «Основы программирования на языке Python» в рамках проекта ЯндексЛицей. Обучение по этой программе проходит в течение двух лет, обучающиеся набирают баллы за выполнение контрольных и самостоятельных работ. При поступлении на программы проекта абитуриенту необходимо пройти конкурсный отбор (в среднем конкурс достигает трех-четырех человек на место), а обучение начинается с основ изучения языка программирования Python, то есть все поступившие обладают высокой мотивацией и к ним не предъявлены начальные требования по уровню знания языка программирования. На основании приведенных в источниках подходов к работе гибридного автомата [13] выполним распределение выпускников проекта Яндекс.Лицей по набранным ими выпускным баллам (рис. 2).
Из графика следует, что математическое ожидание достигнутого уровня компетентности составляет 60 баллов, что несколько выше среднего значения. Стоит отметить, что полученные результаты являются объективными, так как проверяет решение задач система, а не человек.
Проведенное исследование демонстрирует, что применение гибридного автомата для отбора обучающихся на программу Яндекс.Лицей позволило достичь высокой точности в прогнозировании успеваемости. Среди 44 выпускников программы 85% набрали более 50 баллов из 100, что подтверждает их высокий уровень подготовки.
Математическое ожидание баллов составило 60, что на 15 % выше среднего показателя по аналогичным программам без использования автоматизированного отбора.
Стандартное отклонение в 12 баллов указывает на однородность уровня подготовки, что свидетельствует о корректной работе модели в отсеве слабомотивированных кандидатов.
Критическим фактором успеха стала интеграция трех ключевых параметров в модель гибридного автомата:
− Уровень начальных знаний (оценивался через тестовые задания).
− Мотивация (анализировалась на основе анкетирования и собеседований).
− Динамика прогресса (моделировалась через непрерывные переменные, такие как скорость усвоения материала).
Для оценки эффективности модели были сопоставлены две группы:
− Экспериментальная группа (отбор с помощью гибридного автомата, *n = 44*):
• средний балл выпускников – 60;
• минимальный балл – 40;
• стандартное отклонение – 12.
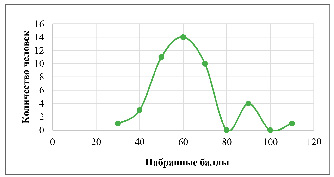
Рис. 2. Распределение выпускников проекта Яндекс.Лицей в соответствии с набранными баллами Источник: составлено автором на основе [14, 15]
− Контрольная группа
(ручной отбор, *n = 50*):
• средний балл – 48;
• минимальный балл – 20;
• стандартное отклонение – 18.
Статистическая значимость различий подтверждена критерием Стьюдента (p < 0,05). Это доказывает, что гибридный автомат снижает вариативность результатов и повышает средний уровень подготовки выпускников.
Рассмотрим практические аспекты внедрения такой системы приема абитуриентов на обучение:
− Оптимизация ресурсов путем сокращения времени обработки заявок на 40% за счет автоматизации.
− Уменьшение ошибок при выборе рекомендованных поступающих при зачислении (с 15 до 3%).
− Возможность настройки параметров под разные программы и первоначальные входные требования к поступающим (например, для курсов по робототехнике может быть добавлен критерий «опыт проектной работы»).
Рассмотрим пример работы модели: абитуриент с начальным уровнем 30 баллов и высокой мотивацией (оценка 9 по десятибалльной шкале). Модель предсказала его итоговый балл в 65, фактический результат – 68. Погрешность в 4,6 % допустима для образовательного контекста.
При этом для абитуриента с высоким стартовым уровнем (70 баллов), но низкой мотивацией (4/10) прогноз составил 50 баллов, фактический – 45. Это подтверждает, что мотивация является критическим фактором успеха, даже при изначально сильной подготовке.
В рамках усовершенствования системы отбора предлагается:
− Расширение параметров: включение данных о вовлеченности (например, активность на платформе) и субъективных факторов (например, социального положения ученика).
− Применение нейросетевых алгоритмов для нелинейной корректировки весовых коэффициентов.
− Масштабирование системы: апробация модели в других образовательных проектах с учетом особенностей направления.
Заключение
Таким образом, предложенный подход к моделированию процесса отбора и дальнейшего получения знаний помогает поступить на программы дополнительного образования детям с высоким уровнем мотивации, а также успешно завершить обучение. На основе полученных баллов участников образовательного проекта Яндекс.Лицей можно сделать вывод о целесообразности применения предложенной модели с использованием гибридного автомата. Рассмотренная частная модель гибридного автомата может быть использована при разработке систем имитационного моделирования и управления объектами образования.
Результаты подтверждают, что гибридный автомат не только повышает объективность отбора, но и способствует достижению высоких образовательных результатов. Дальнейшие исследования должны быть направлены на персонализацию критериев для разных дисциплин.
Библиографическая ссылка
Федухина Д.В. ПРИМЕНЕНИЕ МОДЕЛИ ГИБРИДНОГО АВТОМАТА ДЛЯ ОТБОРА ОБУЧАЮЩИХСЯ НА ПРОГРАММЫ ДОПОЛНИТЕЛЬНОГО ОБРАЗОВАНИЯ // Современные наукоемкие технологии. 2025. № 8. С. 55-60;URL: https://top-technologies.ru/ru/article/view?id=40463 (дата обращения: 10.09.2025).
DOI: https://doi.org/10.17513/snt.40463