Введение
Химико-технологические процессы представляют собой сложные иерархические системы, где каждый уровень требует описания через набор нелинейных уравнений разной степени сложности. В результате их объединения формируется общая система, включающая трансцендентные зависимости и алгебраические уравнения. Даже с использованием современных вычислительных методов решение таких систем остается крайне затратным по времени и вычислительным ресурсам. Это существенно ограничивает их применение в системах автоматизированного управления технологическими процессами (АСУ ТП), где ключевым требованием является высокая скорость обработки данных Значительный вклад во время получения решения вносят вычисления характеристик смесей – доли газовой фазы, вязкости, рассчитываемых на нижних уровнях.
Моделирование химико-технологических систем и процессов (ХПС) математическими методами составляет методологическую основу для технологических расчетов при проектировании, диагностике рабочих параметров эксплуатируемых химических производств и оптимизации их управленческих алгоритмов [1, с. 1–17]. Современные математические модели аппаратов ХПС представляют собой систему нелинейных уравнений, включающую блоки описания материального баланса, массообмена, теплового баланса и парожидкостного равновесия [2].
Уравнения взаимосвязаны между собой параметрами, характеризующими в том числе транспортные свойства химической смеси внутри аппарата. К их числу относятся доля газовой фазы химической смеси, вязкость, плотность и др., для расчета которых также используются нелинейные зависимости [1, c. 35–44]. Время получения решения при сохранении его точности становится определяющим при решении множества задач моделирования ХПС. Расчет транспортных свойств химических смесей, в том числе вязкости, находясь на нижнем уровне модели ХПС, определяет качество и скорость получения общего результата.
Машинное обучение сегодня предлагает эффективные инструменты для быстрого прогнозирования. Многообразие алгоритмов позволяет обрабатывать сложные данные любой структуры, не требуя при этом точного математического описания лежащих в основе процессов, в отличие от классических методов моделирования.
Проведенный обзор научной литературы по машинному обучению позволил систематизировать основные подходы к обучению моделей [3]: обучение без учителя (unsupervised learning) [4], обучение с учителем (supervised learning) [5], обучение с подкреплением, ансамблевые методы, полуконтролируемое обучение [6], многозадачное обучение [7], гибридные подходы [8]. Неконтролируемое обучение (unsupervised learning) [4] характеризуется отсутствием предварительных сведений о категориальной принадлежности объектов в обучающей выборке. В данном подходе алгоритмы автоматически выделяют кластеры объектов, основываясь на метриках сходства, которые определяются через расстояние между векторами признаков в многомерном пространстве. Особый интерес представляют модели, способные выявлять дополнительные свойства кластеров, такие как алгоритм DBSCAN [3]. Этот метод кластеризации по плотности группирует близко расположенные точки данных (имеющие множество соседей в заданном радиусе), одновременно идентифицируя аномалии в разреженных областях признакового пространства. В отличие от предыдущего подхода, контролируемое обучение (supervised learning) требует наличия размеченного датасета, где каждый экземпляр снабжен соответствующей классовой меткой. Данная парадигма особенно востребована при обучении искусственных нейронных сетей, хотя следует отметить, что нейросетевые архитектуры могут обучаться и по другим схемам [5].
Выделяются два подхода к построению и обучению ММО – это гибридное обучение и ансамблевое обучение [8]. Современные исследования подтверждают, что оба подхода к обучению основаны на комбинации различных модельных архитектур. В случае ансамблевых методов возможно использование однотипных алгоритмов, что наглядно демонстрирует алгоритм «случайный лес» [9]. Однако данное условие не является строго обязательным. В отличие от этого, гибридные подходы принципиально требуют сочетания разнородных моделей, включая в некоторых случаях интеграцию алгоритмов машинного обучения с физически обоснованными моделями [8].
Современный инструментарий машинного обучения включает множество разнородных подходов, основанных на различных принципах обучения. Тем не менее применительно к прогнозированию транспортных характеристик полидисперсных углеводородных систем эффективность большинства методов машинного обучения оказывается ограниченной как по числу учитываемых веществ, так и с учетом только одной фазы, например [10].
В современных программных средствах компьютерного моделирования ХПС часто используются интеллектуальные средства. Авторы обзоров [11, 12] показали, что количество исследований в области химии, использующих средства ИИ, увеличилось с нескольких тысяч в 2010 г. до более 60000 в 2021 г. Согласно исследованию J.B. Zachary [13], наибольший интерес в публикациях, посвященных применению искусственного интеллекта в химии, вызывают нейронные сети, теория функционала плотности и метод «случайного леса».
В современных программах моделирования ХПС для расчета вязкости используются различные модели, выбор которых зависит от состава смеси, состояния смеси. Для расчета вязкости можно использовать одну из моделей:
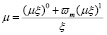, (1)
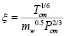, (2)
,
,
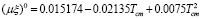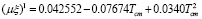где Tcm, Pcm – критические температура и давление, mw – молекулярный вес,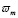 
– фактор ацентричности, 
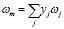, yj – мольная доля вещества в смеси.
Значения критических температуры и давления смеси рассчитываются по степенным зависимостям с дробным показателем степени, например, для модели Соаве – Редлиха – Квонга
,
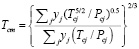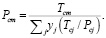(3)
Расчет сложных аппаратов в ХПС проводится итерационно, и на каждой итерации рассчитываются значения транспортных свойств, в том числе и вязкости. Заметим, что модели расчета вязкости смеси рассчитывались на основе мольной доли вещества в смеси, также расчет проводился для обеих фаз смеси. Для получения информации о долях чистых веществ в жидкой и газовой фазах необходимо рассчитывать долю паровой фазы на основе модели расчета парожидкостного равновесия. Здесь различные математические модели – модели Соаве – Редлиха – Квонга, Пенга – Робинсона, модель неслучайных двух жидкостей (NRTL), универсальная квазихимическая модель (UNIQUAC) [1]. Модели расчета значения доли газовой фазы представляют собой совокупность нелинейных уравнений. В итоге для расчета значения вязкости необходимо решить систему нелинейных уравнений, включающих степенные зависимости с дробными показателями степеней и логарифмы [1]. Полученная задача является весьма затратной вычислительно. Очевидно, использование средств быстрого и достаточно точного расчета значения вязкости снизит временные затраты на расчет всего ХПС.
Проведенный анализ научных работ выявил эффективность применения многослойных полносвязных персептронов (МПП) для прогнозирования вязкости и фракционного состава. Следует отметить, что при определенных термобарических условиях и составе смеси может наблюдаться полная гомогенизация системы в газообразном или жидком состоянии, что делает излишним расчет реологических параметров для отсутствующей фазы.
Разработка и внедрение высокоточного метода расчета вязкости широких фракций углеводородов, основанного на применении искусственных нейронных сетей. Данный метод призван преодолеть ограничения существующих эмпирических корреляций и групповых методов расчета, обеспечивая существенное повышение точности прогнозирования и эффективности процесса за счет автоматизированной обработки данных. Конечным результатом работы станет реализация метода в виде специализированного, удобного и надежного программного комплекса, предназначенного для использования в научно-исследовательской и инженерной практике нефтегазовой и нефтехимической отраслей.
Целью исследования является способ расчета вязкости широкой фракции углеводородов с использованием нейронных сетей для повышения точности и эффективности прогнозирования по сравнению с традиционными методами и реализация в виде специализированного программного комплекса.
Материалы и методы исследования
Расчеты и анализ данных проводились с использованием специализированного программного обеспечения. Для разработки алгоритмов и визуализации данных применялся пакет MATLAB. Инженерное проектирование, симуляция технологических процессов выполнялись в среде UNISIM.
В ходе исследования была осуществлена декомпозиция исходной задачи на две последовательные стадии. Первоначально разработан классификационный алгоритм для определения фазового состояния системы, где каждому образцу присваивался один из трех возможных классов: 1 – газовая фаза, 2 – жидкая фаза, 3 – смешанная фаза.
Второй этап – определение вязкостных свойств смеси, где методика расчета дифференцировалась в зависимости от установленного класса фазового состояния системы. Таким образом была построена МПП для реализации первой стадии, MLF_S1, которая будет определять класс принадлежности примера.
Для реализации второй стадии этапа построены три МПП расчета вязкости смеси из каждого класса, MLF_V для первого класса, MLF_L для второго и MLF_M для третьего класса. Предложенная декомпозиция значительно сократила объем вычислений, что способствует снижению параметричности МПП и понижению проблематичности процедуры обучения моделей.
Для обучения МПП выбраны признаки, необходимые для обеспечения полноты представления объектов, а затем построен обучающий набор данных. Реологические характеристики газовых систем демонстрируют выраженную зависимость от давления, тогда как вязкость жидкой фазы преимущественно определяется температурными параметрами.
Таким образом, корректное моделирование реологического поведения требует учета ключевых термодинамических переменных: давления как доминантного фактора для газовой фазы и температуры как основного параметра для жидкой фазы. Объектом исследования служит десятикомпонентная система, включающая следующие соединения: азот, диоксид углерода, сероводород, метан, этан, пропан, изобутан, н-бутан, изопентан и н-пентан. В сочетании с термодинамическими параметрами (давление и температура) это формирует 12-мерное пространство признаков.
Процесс обучения требует формирования четырех независимых обучающих выборок: первая предназначена для тренировки классификатора фазовых состояний, тогда как три остальных используются для построения специализированных регрессионных моделей прогнозирования вязкости, соответствующих каждому из возможных фазовых состояний системы.
Доступные экспериментальные данные о многокомпонентных смесях характеризуются ограниченным объемом выборки и неоднородностью признакового пространства. В связи с этим для генерации данных была использована среда Unisim, где реализована компьютерная модель вспомогательного химико-технологического процесса, позволяющая рассчитывать фазовый состав (долю паровой фазы) и реологические характеристики (вязкость) системы при вариации параметров состава, давления и температуры (рис. 1).
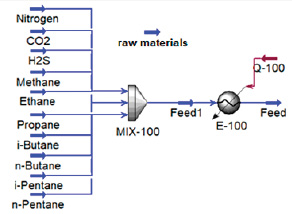
Рис. 1. Вспомогательный вычислительный блок Unisim Источник: составлено авторами
Результаты исследования и их обсуждение
С целью автоматизации процесса формирования данных был создан специализированный программный комплекс DATABANK (рис. 2), генерирующий четыре необходимых набора данных. Архитектура системы включает модуль PLANT, выполняющий следующие функции: передачу состава смеси в поток raw materials, передачу термодинамических параметров (T, P) в теплообменник Е-100, получение расчетных значений от Unisim: доля газовой фазы, вязкость смеси.
Интеграция модуля PLANT с Unisim осуществляется посредством технологии Component Object Model (COM) [14, 15]. Модуль DATA выполняет итеративную генерацию параметров (T, P, состав), передает их в PLANT, получает результаты моделирования и формирует соответствующие наборы данных. Все компоненты системы разработаны на языке MatLab с использованием встроенной поддержки COM-технологии для обмена данными.
Для задачи первой стадии построена МПП классификации MLF_S1, в качестве функции потерь выбрана кроссэнтропия, минимизация осуществлялась методом Левенберга – Марквардта. МПП MLF_S1 имеет один скрытый слой, выходной слой содержит 3 нейрона по числу классов, входной слой – 12 нейронов по числу признаков. Оптимизация гиперпараметров (числа нейронов в скрытом слое, выбор функции активации) проводилась по сетке. После тщательного тестирования различных архитектур наилучшие результаты показала нейросетевая модель со следующими параметрами: скрытый слой из 25 нейронов с функцией активации tanh; продолжительность обучения составила 110 эпох (обусловлено масштабом обучающей выборки, превышающей 800 тыс. образцов).
Анализ графических данных (рис. 3), в том числе матрицы классификации и распределения ошибок, позволяет сделать следующие выводы: количество ошибочных прогнозов крайне незначительно; алгоритм демонстрирует устойчивую сходимость в процессе обучения; модель обладает выраженной способностью к различению классов.
Ключевые преимущества выбранной конфигурации:
1. Оптимальное соотношение сложности модели и вычислительных затрат.
2. Устойчивость к переобучению благодаря регуляризирующему эффекту «tanh-активаций».
3. Репрезентативность оценки качества на крупном датасете.
Для задач аналогичной размерности рекомендуется рассматривать данную архитектуру в качестве основного решения.
На втором этапе для решения поставленных задач разработали три МПП. В частности, для класса 1 построили модель MLF_V с одним скрытым слоем (53 нейрона), дополненную каскадом, подающим входные сигналы не только на скрытый, но и на выходной слои (рис. 4).
Для смеси в жидком состоянии лучшее качество аппроксимации с R = 0,977 показала МПП MLF_L со скрытым слоем из 53 нейронов. Сеть удалось обучить после нормализации входных данных. Для класса смешанной фазы необходимо предсказывать два параметра – вязкость в газовой и в жидкой фазах. Здесь лучшие результаты с R = 0,985 показала МПП MLF_M с каскадом, с 40 нейронами в скрытом слое при нормализации входных данных.
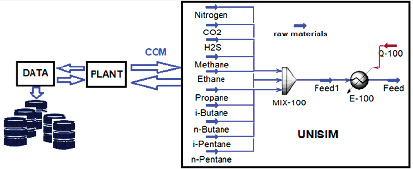
Рис. 2. Структура программного комплекса DATABANK Источник: составлено авторами
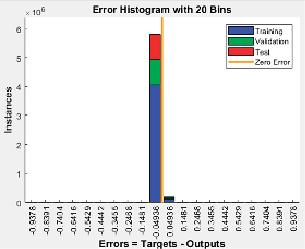
Рис. 3. Матрица ошибок и распределение ошибок классификатора Источник: составлено авторами
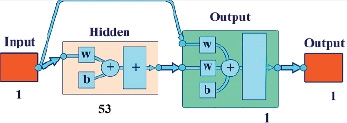
Рис. 4. Структура МПП MLF_V Источник: составлено авторами
Все построенные нейронные сети обучались на датасетах, которые разбивались на обучающее, валидационное и тестовое подмножества по 70, 15 и 15 % от исходного набора соответственно. Потери при обучении не превысили 10-6 при отсутствии переобучения. Для уточнения качества работы построенных МПП были проанализированы результаты работы на промышленном примере, не попавшем ни в один датасет. Отклонения составили не более 0,01 %, что объясняется подготовкой датасетов, обеспечивших репрезентативность данных.
Заключение
Для прогнозирования вязкостных характеристик полидисперсных углеводородных систем был создан специализированный программный комплекс ВЯЗКОСТЬ, разработанный в среде MatLab. Система обеспечивает: интерактивный ввод параметров исследуемой смеси, расчет и вывод значений вязкости, интеграцию обученных нейросетевых моделей.
Предложенная декомпозиция задачи расчета вязкости многокомпонентной смеси позволила использовать несколько небольших нейронных сетей разной архитектуры вместо одной нейросети большой параметричности. Разработанный программный комплекс доказал свою эффективность и надежность, представляя собой мощный инструмент для расчета вязкости широкой фракции углеводородов при моделировании процессов нефтехимии.
Библиографическая ссылка
Лаптева Т.В., Лаптев С.А., Бронская В.В. РАЗРАБОТКА КОМПЛЕКСА НЕЙРОННЫХ СЕТЕЙ ДЛЯ РАСЧЕТА ВЯЗКОСТИ ХИМИЧЕСКОЙ СМЕСИ НА ОСНОВЕ ДЕКОМПОЗИЦИИ ЗАДАЧИ // Современные наукоемкие технологии. 2025. № 7. С. 27-33;URL: https://top-technologies.ru/ru/article/view?id=40437 (дата обращения: 07.08.2025).
DOI: https://doi.org/10.17513/snt.40437