Введение
В настоящее время модели систем массового обслуживания (СМО) находят широкое применение в управлении процессами в телекоммуникациях, логистике, энергетике и многих других секторах экономики. В контексте новой промышленной революции, известной как Индустрия 4.0, принципы теории массового обслуживания также используются в управлении высокоавтоматизированными производствами (например, умными фабриками), большими данными, интернетом вещей, в аддитивных технологиях, беспилотной авиации и т.д.
Многие современные системы и процессы, которые могут быть описаны в терминах теории массового обслуживания, являются многофазными [1, 2]. В системах такого типа каждое требование (заявка) последовательно проходит через несколько этапов (иначе – фаз) обработки, при этом каждый из этапов может представлять собой отдельную операцию или группу операций с одинаковой или различной скоростью обслуживания. Примером такой системы может служить производственный процесс, в котором изготовляемая продукция проходит несколько стадий обработки. В настоящее время классические многофазные системы достаточно хорошо исследованы, системам такого типа посвящено немало научных работ отечественных и зарубежных авторов, например [3, 4].
Кроме многофазности, часто реальные системы характеризуются различной производительностью приборов (каналов, обслуживающих устройств) [5–7]. Неодинаковая скорость работы устройств позволяет учесть различия в сложности операций, сбалансировать нагрузку на систему и, соответственно, избежать перегрузки отдельных этапов. К примеру, на предприятиях, оснащенных роботизированными линиями, системы такого типа позволяют оптимально минимизировать время простоя оборудования. В сфере телекоммуникаций такие СМО дают возможность оперативно реагировать на изменение трафика и предотвращать перегрузки системы. В условиях динамично меняющейся среды, характерной для настоящего времени, системы массового обслуживания с приборами различной производительности обеспечивают большую гибкость и управляемость, что делает их особенно актуальными [8]. Кроме того, при эффективном управлении потоками требований системы такого типа могут обеспечивать большую производительность по сравнению с классическими системами с однотипными приборами [9, 10].
Многофазные СМО с приборами различной производительности встречаются в различных сферах, где процессы обслуживания делятся на несколько последовательных этапов, выполняемых с разной скоростью. Примером такой системы может служить производственная роботизированная линия на заводе, где товары проходят стадии подготовки сырья, основного производства и контроля качества, причем каждое оборудование работает с разной скоростью.
Несмотря на имеющиеся работы, предметом исследования которых являются системы такого типа [11, 12], некоторые вопросы эффективного управления потоками в них в настоящее время исследованы весьма неполно. В частности, автору неизвестны работы, связанные с исследованием областей параметров, при которых системы с приборами различной производительности могут быть эффективнее классических СМО.
В рамках настоящей работы предпринята попытка изучения некоторых функциональных особенностей и закономерностей поведения многофазных СМО с приборами различной производительности. Целью работы является исследование влияния неоднородности приборов на функциональные характеристики многофазной системы массового обслуживания.
Материалы и методы исследования
Рассмотрим k-фазную систему массового обслуживания, на вход которой поступает пуассоновский поток заявок интенсивности λ, λ > 0. Система состоит из n, n > 0 устройств, их количество на всех фазах обслуживания одинаково. Интенсивности приборов равны соответственно μ1,…,μn, при этом μ1,…,μn > 0.
Примем, что система такого типа обладает приборами одинаковой производительности, если
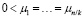 , …,
, …, 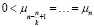 .
.
Иными словами, будем считать, что СМО обладает каналами одинаковой производительности, если их интенсивности равны в каждой из фаз обслуживания. При этом суммарная производительность приборов каждой из фаз может быть различной. В системах с приборами различной производительности будем считать что
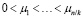 , …,
, …, 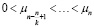 ,
,
то есть в каждой из фаз обслуживания приборы отсортированы по величине производительности, причем суммарная интенсивность приборов в каждой из фаз также может быть различной.
Поступающее в систему требование последовательно проходит через несколько фаз обслуживания, при этом, если требование уже завершило обработку на одной из них, а все каналы в следующей фазе заняты, данная заявка остается на приборе, временно блокируя его работу.
В качестве простейшего примера рассмотрим 2-фазную систему массового обслуживания без функции накопления очереди, состоящую из 4 приборов. На вход системы поступает пуассоновский поток заявок интенсивности λ, λ > 0. Интенсивности приборов равны соответственно μ1,…,μ4, μ1,…,μ4 > 0 (если производительности приборов различны, полагаем, что 0 < μ1 < μ2, 0 < μ3 < μ4).
Для управления потоками в системах с разнородными приборами используются различные алгоритмы распределения заявок, для систем с отказами наиболее эффективным среди которых является направление поступающих требований на свободный канал наибольшей производительности [9]. С учетом этого в рамках настоящей работы при проведении вычислительных экспериментов используется данный алгоритм.
В рамках серии вычислительных экспериментов проведен сравнительный анализ показателей эффективности многофазной системы, обладающей каналами одинаковой производительности в каждой из фаз (μ1 = μ2 = 5; μ3 = μ4 = 4), и систем с каналами различной производительности при различных соотношениях интенсивностей приборов – от незначительной разницы между ними (μ1 = 4,5, μ2 = 5,5; μ3 = 3,5, μ4 = 4,5) до весьма существенной (μ1 = 1, μ2 = 9; μ3 = 0,5, μ4 = 7,5). Выбор значений интенсивностей для разнородных приборов осуществлялся таким образом, чтобы суммарная производительность системы оставалась постоянной. Данные значения в совокупности с различными вариациями входного потока λ позволяют без привязки к определенной реальной системе исследовать общие закономерности функционирования СМО такого типа в широком диапазоне нагрузки
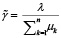 ,
,
как в условиях небольшого напряжения, так и при перегрузке [9]. Такой подход помогает объективно сравнивать показатели систем и выявлять узкие места.
В качестве показателей эффективности рассматриваются p0 – вероятность того, что ни один из каналов обслуживания в системе не занят, то есть система находится в состоянии покоя, и pотк – вероятность того, что вновь прибывшая заявка не сможет получить обслуживание из-за занятости всех каналов. Эти показатели важны для оценки эффективности работы СМО, так как они отражают баланс между ее способностью обрабатывать входящие заявки и уровнем загрузки каналов.
Суммарная производительность каналов во всех рассматриваемых системах равна μ1 + μ2 + μ3 + μ4 = 18.
Параметры исследуемых моделей представлены в таблице 1.
Для проведения вычислительных экспериментов используется программный комплекс AnyLogic [13–15]. Данная среда является достаточно эффективным и удобным инструментом для моделирования и анализа различных типов СМО, включая многофазные системы. Стандартные блоки AnyLogic позволяют легко настраивать параметры разработанных моделей, такие как интенсивность поступления заявок, производительность каналов и иное, что упрощает тестирование различных сценариев и оценку эффективности систем.
Модель 2-фазной системы представлена на рисунке. В данной модели блоки delay и delay1 имеют роль первой фазы обслуживания, delay2 и delay3 – второй фазы. Потоки требований распределяются через блоки selectOutput – selectOutput3.
Таблица 1
Параметры исследуемых моделей
|
μ1 |
μ2 |
μ3 |
μ4 |
||
|
Приборы одинаковой производительности |
СМО-0 |
5 |
5 |
4 |
4 |
|
Приборы различной производительности |
СМО-1 |
4,5 |
5,5 |
3,5 |
4,5 |
|
СМО-2 |
4 |
6 |
3 |
5 |
|
|
СМО-3 |
3,5 |
6,5 |
2,5 |
5,5 |
|
|
СМО-4 |
3 |
7 |
2 |
6 |
|
|
СМО-5 |
2,5 |
7,5 |
1,5 |
6,5 |
|
|
СМО-6 |
2 |
8 |
1 |
7 |
|
|
СМО-7 |
1,5 |
8,5 |
0,5 |
7,5 |
|
|
СМО-8 |
1 |
9 |
0,5 |
7,5 |
|
Примечание: составлено автором.
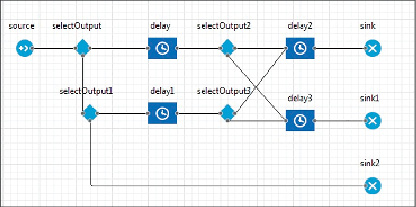
Имитационная модель 2-фазной СМО Источник: составлено автором
Результаты исследования и их обсуждение
В таблице 2 представлены результаты серии вычислительных экспериментов: области эффективности 2-фазной системы с приборами различной производительности по показателю p0. Значения в ячейках таблицы равны p02 – p01 (p02 и p01– вероятности отсутствия заявок в многофазной СМО с каналами одинаковой и различной производительности соответственно). Таким образом, положительные значения в ячейках таблицы указывают на то, что при данных параметрах нагрузки на систему и соответствующих соотношениях в производительности обслуживающих устройств (от незначительной разницы между ними при «СМО-1» и до значимой при «СМО-8») многофазная система с приборами различной производительности является более эффективной, чем система с приборами одинаковой производительности. Отрицательные значения представляют собой разницу между вероятностями для различных конфигураций СМО, а не сами вероятности. Таким образом, отрицательные значения демонстрируют относительную эффективность одной системы по отношению к другой.
Анализ таблицы 2 позволяет выявить некоторые особенности поведения многофазных СМО с приборами различной производительности. Основной вывод заключается в том, что при соблюдении некоторых условий такие системы могут демонстрировать преимущества перед классическими системами с однородными каналами.
Таблица 2
Области эффективности СМО по показателю p0
|
λ |
СМО-1 |
СМО-2 |
СМО-3 |
СМО-4 |
СМО-5 |
СМО-6 |
СМО-7 |
СМО-8 |
|
1 |
0,012 |
0,022 |
0,031 |
0,035 |
0,037 |
0,034 |
0,021 |
0,004 |
|
3 |
0,012 |
0,021 |
0,024 |
0,019 |
0,006 |
-0,026 |
-0,069 |
-0,117 |
|
5 |
0,01 |
0,012 |
0,014 |
0,01 |
-0,009 |
-0,035 |
-0,075 |
-0,104 |
|
7 |
0,004 |
0,005 |
0,006 |
-0,006 |
-0,011 |
-0,032 |
-0,052 |
-0,077 |
|
9 |
0,003 |
-0,001 |
0,003 |
-0,004 |
-0,013 |
-0,028 |
-0,042 |
-0,059 |
|
11 |
0,003 |
0 |
0 |
-0,005 |
-0,012 |
-0,02 |
-0,031 |
-0,045 |
|
13 |
0,003 |
0 |
-0,001 |
-0,006 |
-0,009 |
-0,018 |
-0,024 |
-0,035 |
|
15 |
0,001 |
0 |
-0,001 |
-0,002 |
-0,006 |
-0,01 |
-0,019 |
-0,025 |
Примечание: составлено автором.
Таблица 3
Области эффективности СМО по показателю pотк
|
λ |
СМО-1 |
СМО-2 |
СМО-3 |
СМО-4 |
СМО-5 |
СМО-6 |
СМО-7 |
СМО-8 |
|
1 |
0,001 |
0,002 |
0,003 |
0,003 |
0,003 |
0,002 |
-0,002 |
-0,004 |
|
3 |
0,001 |
0,003 |
0,002 |
-0,004 |
-0,013 |
-0,03 |
-0,062 |
-0,073 |
|
5 |
0,001 |
0 |
0,002 |
-0,004 |
-0,022 |
-0,047 |
-0,084 |
-0,096 |
|
7 |
-0,001 |
-0,003 |
-0,002 |
-0,017 |
-0,03 |
-0,053 |
-0,076 |
-0,093 |
|
9 |
-0,001 |
-0,008 |
-0,005 |
-0,016 |
-0,028 |
-0,052 |
-0,074 |
-0,09 |
|
11 |
0,001 |
-0,008 |
-0,009 |
-0,019 |
-0,032 |
-0,047 |
-0,071 |
-0,082 |
|
13 |
0,001 |
0 |
-0,009 |
-0,016 |
-0,025 |
-0,045 |
-0,061 |
-0,072 |
|
15 |
-0,001 |
-0,006 |
-0,007 |
-0,014 |
-0,026 |
-0,037 |
-0,058 |
-0,067 |
Примечание: составлено автором.
При низкой нагрузке (λ < 5) системы с приборами различной производительности в основном показывают лучший результат по сравнению с однородными системами. Эта тенденция наиболее ярко проявляется при значениях интенсивностей приборов в «СМО-2» – «СМО-6» (См. параметры в таблице 1). По мере увеличения загрузки эффективность систем такого типа начинает снижаться, причем быстрее всего это происходит в системах «СМО-7» – «СМО-8». Однако даже в этих условиях система с малой неоднородностью приборов «СМО-1» продолжает показывать небольшие преимущества. Данное обстоятельство позволяет сделать вывод о том, что системы с малыми различиями в производительности остаются устойчивее к увеличению нагрузки. При высокой загрузке почти все многофазные системы с приборами различной производительности теряют свою эффективность, демонстрируя худшие результаты по сравнению с однородными системами.
Также обращает на себя внимание то, что характер распределения представленных областей эффективности во многом совпадает с распределением областей эффективности классических однофазных СМО, рассмотренных ранее, например в [8].
В таблице 3 представлены области эффективности многофазной СМО по показателю pотк. Значения в ячейках данной таблицы равны pотк1 – pотк2 (pотк1 и pотк2 – вероятность того, что вновь прибывшая заявка не сможет получить обслуживание из-за занятости всех каналов в СМО с каналами одинаковой и различной производительности соответственно).
По данным таблицы 3, при интенсивности входного потока λ = 1 по показателю p0 многофазная система с неэквивалентными каналами эффективнее своего классического аналога на 0,035, в то же время по показателю pотк при тех же исходных параметрах система с неэквивалентным каналами опережает систему с каналами одинаковой производительности на 0,003. Данное значение находится в пределах погрешности средств имитационного моделирования. При этом области эффективности систем с приборами различной производительности практически идентичны для обоих исследуемых показателей. Несмотря на незначительную разницу в показателях pотк, данное обстоятельство должно приниматься во внимание при проектировании или моделировании СМО.
Выводы
Неоднородность приборов оказывает существенное влияние на функциональные характеристики многофазных систем массового обслуживания. На основе проведенных вычислительных экспериментов с использованием программного комплекса AnyLogic установлено, что многофазные СМО с неоднородными приборами способны обеспечивать более высокую производительность по сравнению с классическими системами. Наиболее выраженно это проявляется при низкой загрузке системы и относительно небольших различиях в производительности каналов. Это связано, в первую очередь, с гибкостью распределения требований между обслуживающими устройствами. Кроме того, выявлено, что многофазный характер обслуживания заявок дополнительно усиливает влияние неоднородности приборов на общую производительность системы.
Результаты работы могут найти практическое применение в сфере телекоммуникаций, промышленности и логистики, способствуя созданию более эффективных моделей обслуживания. Использование данных выводов может развить потенциал для повышения конкурентоспособности предприятий и организаций, внедряющих передовые технологии управления процессами массового обслуживания.
Данные результаты хорошо согласуются с выводами, ранее полученными для однофазных систем, что подтверждает универсальность выявленных принципов. Это создает основу для продолжения исследований в данном направлении. Для дальнейшего развития темы видится возможным расширить область исследований, включив в нее модели с большим количеством фаз и каналов, а также построить соответствующие решающие правила для увеличения пропускной способности систем такого типа.
Финансирование
Библиографическая ссылка
Самерханов И.З. МНОГОФАЗНЫЕ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ С ПРИБОРАМИ РАЗЛИЧНОЙ ПРОИЗВОДИТЕЛЬНОСТИ // Современные наукоемкие технологии. 2025. № 5. С. 68-73;URL: https://top-technologies.ru/ru/article/view?id=40392 (дата обращения: 03.02.2026).
DOI: https://doi.org/10.17513/snt.40392



