Введение
Важно отметить, что наличие мутагенных и канцерогенных веществ в рабочей среде подчеркивает необходимость регулярного мониторинга уровня загрязнения. Это создает потребность в использовании группы роботов-лаборантов (РЛ) на химических предприятиях, которые выполняют специфические задачи на технологических объектах в разные временные промежутки [1; 2, с. 201; 3]. Ошибки в работе бригады РЛ могут привести к серьезным последствиям.
Цель исследования – разработка теории для решения задач гарантированного нелинейного программирования, направленной на управление группой роботов-лаборантов. Создание новых алгоритмов управления, учитывающих случайные воздействия, и обеспечение технических требований с заданной вероятностью.
Материалы и методы исследования
В процессе управления бригадой РЛ в рамках роботизированных систем управления важно определить задачи, выполняемые отдельным роботом-лаборантом, а также установить заданное время [4–6] для обслуживания конкретных технологических объектов.
Методы используют имитационное моделирование, теорию оптимального управления, статистику. В работе развиты теоретические основы решения задач нелинейного программирования с эквивалентной детерминированной задачей. Эффективность распределения задач между РЛ часто зависит от времени, отведенного роботам на выполнение этих задач. Например, более частый забор проб для лабораторного анализа в роботизированных автоматизированных системах управления позволяет быстрее корректировать управляющую программу, что, в свою очередь, повышает эффективность их работы [7–9]. В условиях значительного изменения диапазона времени работы робота-лаборанта наблюдается, что увеличение частоты забора проб приводит к снижению темпов роста экономического эффекта. Высокая частота отбора проб и дальнейшее ее увеличение оказывает лишь незначительное влияние на результаты. Это указывает на то, что в условиях больших колебаний времени загрузки робота-лаборанта целевая функция, отражающая эффективность технологического процесса, проявляет нелинейную зависимость от частоты забора проб [10–12]. В таком случае задачи минимизации времени функционирования РЛ относятся к классу нелинейных задач оптимизации [13–15].
Результаты исследования и их обсуждение
Рассмотрим задачу гарантированного нелинейного программирования с учетом случайной величины v:
Q(U) = f(U) + v, (1)
где U = (U,...,Un), f(U) – нелинейная функция,
U – управляющие воздействия (силы, моменты, создаваемые приводами робота).
Технические (гарантируемое отсутствие столкновений звеньев манипулятора робота между собой и с препятствием (технологическое оборудование, трубопроводы, запорная арматура, робот-лаборант и др.) и технологические (параметры продуктов (полупродуктов), сырья, среды) условия имеют вид
φ(U) = ψi(U) + vi ≥ 0, i = 1,2,...,m, (2)
где ψi(U) – нелинейная функция, vi – случайная величина.
Считаем, что случайные величины v1,..., vm независимы, не зависят от вектора U управляющих воздействий и заданы своими известными плотностями распределения ω(v), ωi(vi).
Тогда задача определяется так: найти вектор u* ∈ U, и здесь минимизируется математическое ожидание функции (1):
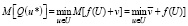 , (3)
, (3)
где v – математическое ожидание случайной величины v, и вероятность P выполнения условий (2) не ниже:
P[ψi(U) + vi ≥ 0] ≥ σi , i=1,2,...,m, (4)
где σi – заданное значение вероятности выполнения i-го технологического условия (2) и Ui ≥ 0.
Задача (3), (4), задача нелинейного надежного программирования, определена в виде: определить вектор u* ∈ U, здесь минимизируется целевая функция (чаще всего в качестве целевой функции используют энергетические затраты, минимальное количество движений звеньев манипулятора):
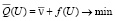 (5)
(5)
и удовлетворяются ограничения
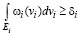 , i=1,...,m. (6)
, i=1,...,m. (6)
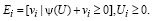 (7)
(7)
Задачей эквивалентности является задача линейного программирования: найти n-мерный вектор U = (u1,...,un), здесь минимизируется значение целевой функции:
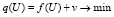 (8)
(8)
и ограничениях
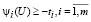 , (9)
, (9)
определяется:
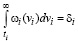 , Ui ≥ 0. (10)
, Ui ≥ 0. (10)
Теорема 1.
Задача надежного нелинейного программирования (5)–(7) с суммируемой случайной величиной тождественна эквивалентной задаче линейного программирования (8)–(10).
Доказательство.
Для задачи нелинейного программирования (5)–(7) условия (6) выполняются в том случае, если
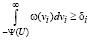 . (11)
. (11)
Параметр ti , определится из условия
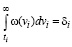 . (12)
. (12)
Если для ti условие (12) выполнено, в том случае (11) тоже будет выполнено, если
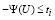
или 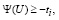
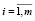 .
.
Так, в этом случае с учетом (12):
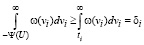 .
.
Соответственно, условия (9), (10) эквивалентны условиям (6), (7) задачи управления, целевые функции (8) и (5) совпадают.
Теорема 1 доказана.
Задача надежного нелинейного программирования с суммированной случайной величиной преобразована в детерминированную задачу нелинейного программирования (8)–(10) с ограничением (9), где используется величина ti, определяемая на основе (12). Теперь обратим внимание на задачу нелинейного программирования с мультипликативным вхождением случайной величины.
Рассматриваем задачу оптимизации, в которой целевая функция имеет вид
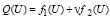 , (13)
, (13)
где f1(U) и f2(U) – нелинейные функции; v – случайная величина.
Ограничения имеют следующую форму:
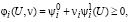 i = 1,2,...,m, (14)
i = 1,2,...,m, (14)
где 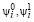 – нелинейные функции и Ui ≥ 0, i = 1,2,...,m.
– нелинейные функции и Ui ≥ 0, i = 1,2,...,m.
Выяснилась задача надежного управления.
Найти вектор U* ∈ U, при котором минимизируется математическое ожидание функции (13):
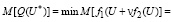
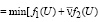 . (15)
. (15)
Вероятность Р выполнения условий (14) – не ниже значений δi:
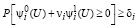 (16)
(16)
и Ui ≥ 0, i = 1,2,...,m. (17)
Тогда задача надежного управления (15)–(17), при котором принимает минимальное значение целевой функционал обозначится:
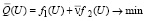 , (18)
, (18)
где v – математическое ожидание случайной величины v, и удовлетворяются ограничения
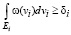 , (19)
, (19)
где 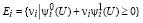 и Ui ≥ 0.
и Ui ≥ 0.
Эквивалентной задачей будем называть следующую задачу нелинейного программирования.
Определить n-мерный вектор
U = (U1, U2,..., Un),
при котором принимает минимальное значение целевая функция:
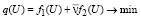 (20)
(20)
при удовлетворении ограничений
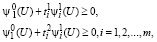 (21)
(21)
и 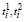 определяются из соотношений
определяются из соотношений
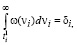
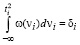 , (22)
, (22)
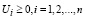 .
.
Определилась следующая вспомогательная лемма.
Лемма 1.
Имеем в виду, что множества Û1, Û2 определяются следующими неравенствами:
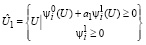 , (23)
, (23)
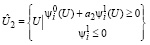 , (24)
, (24)
и а1 , а2 – постоянные величины.
Объединение множеств Û1 ⋃ Û2 тождественно множеству Û, которое определяется соотношениями
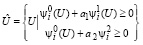 (25)
(25)
Доказательство.
Для доказательности тождественности Û ≡ Û1 ⋃ Û2, доказываем следующее утверждение: для любого U справедливо
U ∈ Û → U ∈ Û1 ⋃ Û2, (26)
U ∈ Û1 ⋃ Û2 → U∈Û. (27)
Так как выполнение (26) очевидно, необходимо доказать лишь соотношение (27).
Авторы полагают:
а1 ≤ а2. (28)
1. Рассматривается вариант, когда:
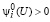 . (29)
. (29)
А. Имеется U ∈ Û. Докажем, что U ∈ Û, и удовлетворяется условие (25), первое условие (25) совпадает с первым условием (23), доказываем, что второе условие (25) тоже выполняется.
Имеем а1 не отрицательно, с учетом (28) имеет место
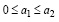 (30)
(30)
с учетом (29):
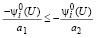 . (31)
. (31)
Из второго неравенства (23) и (31) имеем
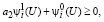
что равносильно выполнению второго неравенства в (25).
Пусть а1, а2 удовлетворяют соотношениям
a1 < 0 ≤ a2, (32)
с учетом (26) имеем
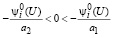 . (33)
. (33)
Из неравенств (23) и (33) получаем
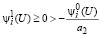 ,
,
что равносильно выполнению второго неравенства в (25).
Таким образом, а1, а2 удовлетворяют соотношениям
а1 ≤ а2 < 0, (34)
с учетом (28) имеем
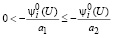 . (35)
. (35)
Из неравенства (23) с учетом (34) имеем
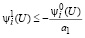 , (36)
, (36)
а, если с учетом (35):
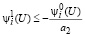 ,
,
то есть 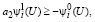
это соответствует выполнению условия неравенства (25).
Таким образом, во всех случаях при выполнении (29) справедливо
U ∈ Û1 → U ∈ Û. (37)
Б. Допустим условие (28) соблюдается, но U ∈ Û2. Докажем, что и в этом случае U ∈ Û1, если второе условие (25) совпадает с первым условием (24), тоже выполняющимся по условию, необходимо доказать только выполнение первого неравенства из (25).
Пусть а1 не отрицательно, то есть с учетом (30) и (29) реально соотношение (31). В связи с чем из первого неравенства (24) имеем
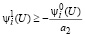 . (38)
. (38)
Из (38) с учетом (31) следует
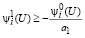 или
или 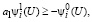
это соответствует выполнению первого неравенства в (25).
Пусть для а1, а2 выполняются соотношения (32), (33). В связи с чем из второго неравенства (24) с учетом (33) имеем
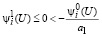 . (39)
. (39)
Видно, что из (38) следует с учетом a1 ≤ 0 выполнение первого неравенства (25):
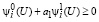 .
.
И, наконец, имеет место (34) и (35). В связи с чем из второго неравенства (24) получаем 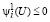 или учитывая (35)
или учитывая (35) 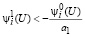 , это при а1 < 0 соответствует выполнению первого неравенства (25)
, это при а1 < 0 соответствует выполнению первого неравенства (25)
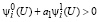 .
.
Таким образом, во всех случаях при выполнении (29) справедливо:
U ∈ Û2 → U ∈ Û. (40)
Из формул (37) и (40) имеем с 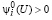
U ∈ Û1 ⋃ Û2 → U ∈ Û. (41)
2. Рассмотрим случай, когда
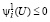 . (42)
. (42)
А. Здесь справедливо соотношение
0 ≤ а1 ≤ а2. (43)
Из первого уравнения (24) следует:
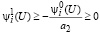 ,
,
то есть система (24) противоречива и Û2 пусто.
То есть для доказательства (27) следует доказать, что
U ∈ Û2 → U ∈ Û. (44)
Из (42), (43) имеем
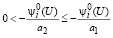 . (45)
. (45)
Допустим U ∈ Û1. В этом случае из первого неравенства (23) имеем
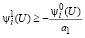 или
или
с учетом (45) 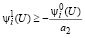 ,
,
это соответствует выполнению второго условия (25). Видно, что первое условие (25) выполняется в силу совпадения с первым условием (23) поэтому имеем
U ∈ Û2 → U ∈ Û.
Б. Пусть справедливо соотношение
а1 < 0 ≤ а2. (46)
В этом случае из первого неравенства (23) следует
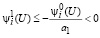 , (47)
, (47)
что противоречит второму неравенству (23) и Û1 пусто.
Из первого неравенства (24) имеем
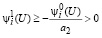 , (48)
, (48)
что противоречит второму неравенству (24) и Û2 пусто. Таким образом Û1 ⋃ Û2 пусто.
При этом множество (25) также пусто, так как первое неравенство (24) может быть представлено в виде (47), а второе – в виде (48). Между тем система (47), (48) имеет противоречие.
В. Рассмотрим случай, когда
а1 ≤ а2 < 0. (49)
Здесь система (23) противоречива, и множество Û1 пусто, что для доказательства (27) необходимо доказать
U ∈ Û2 → U ∈ Û.
Из (42) и (49) имеем
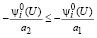 .
.
Если U ∈ Û2, то в этом случае из первого неравенства (24) следует
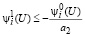 и
и 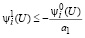 ,
,
то есть первое неравенство (25) выполняет
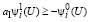 .
.
Так как второе условие (25) совпадает с первым условием (24), которое выполняется по предположению, утверждение U ∈ Û2 → U ∈ Û выполнено.
Из (43), (49) следует, что всегда имеет место
U ∈ Û1 ⋃ Û2 → U ∈ Û. (50)
Из (43) последует, что при значениях 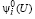 все условия (25), (26) выполняются.
все условия (25), (26) выполняются.
Лемма 1 доказана.
Следствие 1.
В том случае, если при 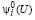 имеет место соотношение
имеет место соотношение
0 ≤ а1 ≤ а2, (51)
множество Û1 ⋃ Û2 тождественно множеству
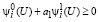 . (52)
. (52)
Доказательство.
Согласно леммы 1 множество Û1 ⋃ Û2 в этом случае тождественно множеству Û1, определяемому неравенствами (24):
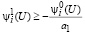 , (53)
, (53)
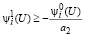 . (54)
. (54)
Так как при 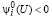 и выполнении (51) имеет место (43), неравенство(53) поглощается неравенством (54).
и выполнении (51) имеет место (43), неравенство(53) поглощается неравенством (54).
Следствие 1 леммы 1 является доказанным.
Теорема 2.
Задача надежного нелинейного программирования в состоянии мультипликативного вхождения случайной величины (18)–(19) является тождественной эквивалентной задаче (20)–(21).
Доказательство.
Учитывая, что целевые функции задач совпадают, для доказательства тождественности задач (18)–(19) и (20)–(21) авторам достаточно доказать тождественность для условий (19) и (21).
Технологические ограничения (14), очевидно, могут быть заданы в виде
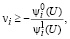 если
если 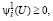 (55)
(55)
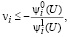 если
если 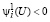 . (56)
. (56)
При этом (19) может быть переформулировано в следующем виде:
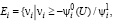 если
если 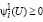 (57)
(57)
и 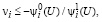 если
если 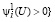 .
.
С использованием (57), условие (19) задачи надежного управления возможно записать в тождественном виде:
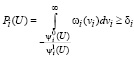 ,
,
если 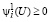 (58)
(58)
и возможно так
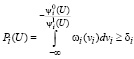 ,
,
если 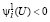 . (59)
. (59)
где Pi(U) – вероятности выполнения i-го условия.
Пусть 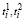 определяются из соотношений
определяются из соотношений
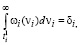
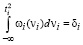 . (60)
. (60)
В этом случае, если при 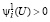 выполняется неравенство
выполняется неравенство
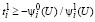 , (61)
, (61)
где 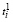 определяется (60), имеет место:
определяется (60), имеет место:
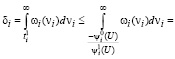
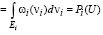 ,
,
то есть при выполнении системы
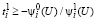 , (62)
, (62)
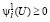 ,
,
условие (19) выполнено.
Аналогично, пусть 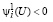 и пусть выполняется
и пусть выполняется
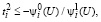 (63)
(63)
где 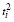 определяется (60).
определяется (60).
В этом случае имеет место в соответствии с (60), (59):
то есть при выполнении системы
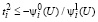 ,
,
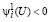 , условия (19) также выполняются. Однако, согласно лемме 1, объединение множества Û1, определяемого (62) и множества Û2, определяемого (64), тождественно множеству Û, определяемого (25). Теорема 2 доказана.
, условия (19) также выполняются. Однако, согласно лемме 1, объединение множества Û1, определяемого (62) и множества Û2, определяемого (64), тождественно множеству Û, определяемого (25). Теорема 2 доказана.
Заключение
Созданная теория решения задач с гарантированным результатом позволяет эффективно планировать деятельность групп роботов, обеспечивая выполнение технических и технологических ограничений с вероятностью не ниже заданного уровня. Действительно, целевая функция и ограничения представляют собой случайные величины. При этом имеет место необходимость в рассмотрении и решении задач гарантированного оптимального управления группой роботов. Сформулированные теоремы доказывают тождественность задач надежного нелинейного программирования эквивалентным, решение которых упрощает реализацию программ управления. Проведенные исследования и полученные результаты тождественны результатам предыдущих исследований, связанных с процессами производства фосфатов и органических диазокрасителей.
Библиографическая ссылка
Калинин В.Ф., Погонин В.А. ЗАДАЧИ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ПРИ ПЛАНИРОВАНИИ РАБОТЫ РОБОТОВ-ЛАБОРАНТОВ // Современные наукоемкие технологии. 2025. № 5. С. 48-54;URL: https://top-technologies.ru/ru/article/view?id=40389 (дата обращения: 03.02.2026).
DOI: https://doi.org/10.17513/snt.40389



