Введение
Квантовое оптимальное управление включает в себя семейство алгоритмов формирования импульсов, которые направлены на раскрытие полного потенциала различных квантовых технологий. Оно основывается на теории управления в более общих терминах, которая развивается на стыке прикладной математики, инженерии и физики и касается манипулирования динамическими процессами для реализации конкретных задач. Основная цель состоит в том, чтобы изучаемая динамическая система работала оптимально и достигала своих физических пределов, удовлетворяя ограничениям, налагаемым имеющимися устройствами [1].
Оптимальное управление является важным приложением машинного обучения и оптимизации. Между тем в последних работах было показано, что важные сведения о глубоком обучении можно получить, интерпретируя процесс обучения глубокой нейронной сети как дискретизацию задачи оптимального управления [2]. В последние десятилетия, после появления квантовых компьютеров, оптимальное управление квантовыми системами привлекло значительное внимание. Это объясняется тем, что квантовые свойства во многом определяют многие из последних достижений в различных отраслях промышленности.
Известно, что свойства квантового оптимального управления лучше всего комбинировать с помощью внешних средств управления. Алгоритмы квантового оптимального управления (КОУ), использующие компьютерное моделирование для определения желаемых управляющих переменных, стали важным направлением в данной предметной плоскости. Сферы приложения КОУ также проявили себя в недавних квантовых вычислениях и квантовых информационных технологиях [3]. Например, парадигма КОУ имеет хорошие связи с вариационными квантовыми алгоритмами и квантовым машинным обучением. Еще одно интересное наблюдение заключается в том, что квантовое управление способно подавлять декогеренцию.
В контексте вышеизложенного все более очевидно, что эффективный алгоритм для квантовых задач оптимального управления может оказывать влияние далеко за пределами тех областей, в которых он возник. Таким образом, более детальное исследование квантовых алгоритмов, которые рассматриваются как «рабочие лошади» квантовых вычислений нынешней эпохи, является актуальной научно-исследовательской задачей, которая и предопределила выбор темы данной статьи.
Цель исследования заключалась в анализе и рассмотрении различных квантовых алгоритмов для квантового оптимального управления.
Материалы и методы исследования
В работе применены методы систематического обзора литературы, контент-анализа. Всесторонний поиск осуществлялся в соответствии с рекомендациями PRISMA и проводился в базах Scopus, Web of Science и Google Scholar за период с 2022 по 2025 г. Литература для такого обзора отбиралась в базах данных на основании количества цитирований публикаций, импакт-фактора, а также индекса Хирша журналов. Кроме того, был включен индекс статей, связанных с цитируемой темой. Эти базы данных были выбраны в соответствии со следующими требованиями: база данных представляет собой журналы общего назначения с большим количеством статей, база данных допускает полноформатный поиск или поиск только в определенных областях работ, является одной из самых релевантных в исследовательской области компьютерных наук, база данных доступна без дополнительной платы.
При работе над этим систематическим обзором литературы использовался Parsifal для управления отслеживаемостью и Mendeley в качестве библиографического менеджера. С другой стороны, для структурирования данного исследования были использованы два библиографических обзора, один из которых рассматривает квантовые вычисления в общем аспекте, а другой – в более конкретном контексте квантового машинного обучения. Для поиска использовались такие строки запросов, как «квантовый алгоритм», «квантовая оптимизация» или «квантовая нейронная сеть», «квантовые вычисления», «квантовая физика».
В практической части исследования использовались методы численного оптимального управления и обучения с подкреплением.
Результаты исследования и их обсуждение
Разработка новых алгоритмов, направленных на снижение эффектов шума и декогеренции, представляет собой одно из ключевых направлений исследований в современной квантовой информатике. Над созданием новых алгоритмов, необходимых для ослабления эффектов шума и декогеренции, трудятся такие авторы как Chun-Ling Zhang, Xiu-Min Lin [4], А.С. Булдаев [5].
В работах Gui-Long Jiang, Wen-Qiang Liu [6] и Neel Kanth Kundu, Prabhu Babu [7] отмечено, что комплексный анализ ошибок квантовых алгоритмов позволяет проводить оценку суммарной погрешности на разных этапах вычислительных процессов, таких как конечно-размерное представление функций управления, дискретизация уравнений Шрёдингера, численные методы интегрирования и оптимизационные процедуры. Исследование возможностей интеграции подходов машинного обучения и квантовой механики, включая применение методов машинного обучения для повышения эффективности управления квантовыми системами и использования принципов квантовой механики для улучшения алгоритмов машинного обучения, занимает важное место среди актуальных научных проблем, раскрытию данного направления посвятили свои труды Б.О. Волков [8], Jonathan Franceschi, Andrea Medaglia [9].
Заслуживает внимания всесторонний анализ ошибок квантового алгоритма, с целью проведения оценки суммарной погрешности различных этапов вычислений, таких как конечно-размерное представление функции управления, дискретизация уравнения Шредингера, численная квадратура и оптимизация, который проводят в своих трудах С.М. Гушанский, В.И. Божич, В.С. Потапов [10].
В последнее время значительные усилия ученых и исследователей [11–13] были направлены на разработку анзацев, сохраняющих симметрии гамильтониана задачи. Целью стратегий, сохраняющих симметрию, является ограничение вариационного поиска небольшим интересующим пространством, что в принципе может улучшить вероятность сходимости к целевому состоянию с меньшим количеством итераций оптимизатора. Также следует отметить, что проводятся параллельные эксперименты и изыскания, задачей которых является создание анзаца, который выходит за рамки методов, сохраняющих симметрию, с помощью введения набора унитариев, нарушающих симметрию гамильтониана задачи [14]. Для этого авторы заимствуют идеи из теории квантового оптимального управления, где быстрые и высокоточные операции достигаются путем добавления к гамильтониану зависящих от времени членов, нарушающих симметрию. Сфокусировавшись на фермионных системах, такие члены включаются в анзац, похожий на эволюцию времени, чтобы получить квантово-оптимальный анзац, вдохновленный контролем.
Soohyun Park, Joongheon Kim [15] и Gui-Long Jiang, Wen-Qiang Liu, Hai-Rui Wei [16] в своих публикациях рассмотрели существующие исследования ландшафта оптимизации гибридных квантово-классических алгоритмов, состоящих из квантового анзаца и классического оптимизатора. В широком представлении, которое простирается от небольших квантовых систем управления до средне- и крупномасштабных квантовых схем, учеными отмечено, что наблюдается морфологический переход ландшафта, когда оптимизатор превращается из ресурсоизбыточного в ресурсонедостаточный по отношению к экспоненциально растущему размеру анзаца.
Как квантовые вычисления, так и моделирование являются сложными задачами квантовой инженерии, требующими высокоуровневых манипуляций с квантовой динамикой. Для этого среди математических инструментов незаменимыми становятся алгоритмы оптимального управления [17]. Они прошли путь от принципов и ранних реализаций, спектроскопических приложений до продвинутых численных алгоритмов для перехода из состояния в состояние и синтеза квантовых ворот, как показано в работах [18].
Также следует отметить результаты анализа возможных областей перекрытия областей машинного обучения и квантовой механики [19], причем как с точки зрения использования алгоритмов машинного обучения для улучшения понимания и управления квантовыми системами, так и с позиции того, как свойства квантовой механики могут применяться для улучшения алгоритмов машинного обучения.
В то же время, несмотря на активный интерес ученых к рассматриваемой проблематике, новизна данной сферы исследования предполагает еще широкий круг дискуссионных и малоисследованных вопросов. Так, например, из-за различных источников ошибок, включая дискретизацию, оценку градиента и ошибки оптимизации, а также невыпуклость целевой функции, оптимизация сложности с использованием современных квантовых алгоритмов является нерешенной задачей. Кроме того, в дальнейшем развитии и усовершенствовании нуждаются методы численного оптимального управления и обучения с подкреплением, с тем чтобы обеспечить лучшую точность и упростить процесс принятий решений.
Также к числу мало проработанных вопросов относятся трудности, связанные с оптимизацией сложности при использовании современных квантовых алгоритмов, обусловленные различными источниками ошибок (такими как дискретизация, оценка градиентов и ошибки оптимизации), а также невыпуклой структурой целевых функций. Важным направлением будущих разработок являются методы численного оптимального управления и обучения с подкреплением, которые должны быть усовершенствованы для повышения точности и упрощения процедур принятия решений.
Итак, отметим, что квантовое управление предполагает предоставление пользователю набора зависящих от времени параметров, необходимых для управления динамической квантовой системой таким образом, чтобы она выполняла определенную задачу [20]. В свою очередь, теория оптимального управления является областью прикладной математики, которая представляет собой мощный инструмент, позволяющий найти методы управления, которые дают возможность динамической системе развиваться для достижения заданной цели [21].
Многие квантовые алгоритмы, такие как известные методы поиска скрытой подгруппы, эффективно решают задачу благодаря использованию схемной модели, которая требует высокой точности выполнения операций (так называемого «порога коррекции ошибок»). Однако поиск альтернативных и более устойчивых подходов привел к развитию топологических квантовых вычислений с использованием анионных квазичастиц, которые связаны с теорией кос. Это происходит потому, что траектории этих частиц в трехмерном пространстве-времени формируют структуры, способные функционировать как квантовые логические элементы. Эти элементы имеют преимущества перед традиционной схемной моделью, так как они менее подвержены ошибкам.
При исследовании взаимосвязей между топологическими и стандартными квантовыми вычислениями обнаружилось, что представления групп кос, используемые в топологическом подходе, могут быть полезны не только для работы с анионными структурами, но и для вычисления инвариантов узлов и других геометрических объектов, например полинома Джонса [22]. Таким образом, существует продуктивное взаимодействие между топологической и схемной моделями, основанное на представлении операций над узлами и связями.
Учитывая вышесказанное, одним из многообещающих направлений развития квантовых алгоритмов может стать использование тепловых ансамблей для приближенного вычисления следа унитарной матрицы. Этот подход открывает новые возможности в области квантовой теории узлов и ее применения в задачах оптимального управления, поскольку позволяет эффективно оценивать полиномы Джонса по ряду параметров.
Рассмотрим данный алгоритм более подробно.
Поскольку узлы с разными полиномами Джонса явно неэквивалентны (в то время как обратное не выполняется), эффективные квантовые алгоритмы, определяющие след унитарных узлов, могут быть очень полезны. Для решения классически трудной задачи NP-класса, связанной с определением эквивалентности двух узлов (то есть возможностью преобразования одного узла в другой с помощью ходов Райдмейстера и тривиальных преобразований), можно воспользоваться полиномами Джонса. Полиномы Джонса позволяют различить узлы, если они действительно различаются, предоставляя эффективный способ проверки эквивалентности узлов, тех, которые не меняют число пересечений [23].
Алгоритм Ахаронова для получения полинома Джонса использует след некоторого унитарного представления соответствующей группы кос. Здесь группа кос с n нитями, Bn, порождена своими n – 1 генераторами, представляющими правосторонние скрутки {σ1, σ2,...,σn-1}. Для оценки следа удобнее всего использовать связь с алгеброй Темперли – Либа и ее унитарным представлением ρ по формуле
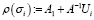
где –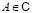 
модуль единицы, Ui – вещественная симметрия, а σi – генератор группы кос, связанной с интересующим узлом.
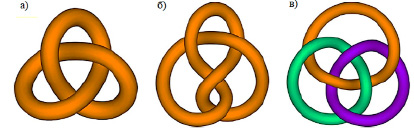
Стандартные узлы, относящиеся к группе кос с тремя нитями B3: (а) узел «трилистник может быть представлен элементом группы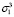 
, (б) узел «восьмерка» – элементом 
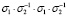и (в) Борромеевы кольца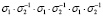 
Далее, представляется целесообразным обратить внимание на группу трехпрядевых кос B3, порожденную элементами {σ1,σ2}. Она включает в себя известные стандартные узлы «трилистник» (вплоть до добавления окружности, расходящейся с узлом), «восьмерку» и «борромеевы кольца», показанные на рисунке.
В унитарном (модель пути) представлении B3 получаются следующие унитарии, содержащие θ (связанные с переменной A скобки и полиномом Джонса):
.
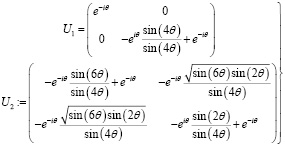Теперь, чтобы получить след Ui с помощью квантового измерения, следует увеличить квантовый регистр на один анцильный кубит. Тогда унитарный Ui переводится в управляемый унитарный относительно анксилла следующим образом:
.
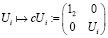На основе тепловых ансамблевых состояний
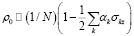
c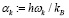 
можно подготовить подходящее начальное состояние с z-намагниченностью на естественном изобилии 13C, используемом в качестве кубита. С этими условиями легко перейти к трем заключительным шагам алгоритма:
подготовка:
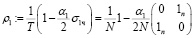
ρ1 эволюционирует под действием сигнатурной последовательности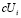 
, характерной для данного узла. Это дает общую сумму:
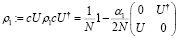
измерение матожидания фазово-чувствительного оператора обнаружения ансамбля
,
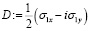чтобы получить
.
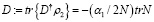Таким образом, преимуществом описанного выше алгоритма для квантового оптимального управления является то, что синтез квантовых ворот или перенос состояний может быть достигнут с оптимизированной точностью для заданных экспериментальных настроек, независимо от того, предполагается ли реализация через чистые состояния или нет.
Отдельного внимания заслуживает вариационный квантовый алгоритм, центральным элементом которого является схема подготовки состояний, также известная как анзац или вариационная форма [24].
Так, например, может использоваться аппаратно-эффективный анзац (HEA), который опирается на вентили, присущие квантовому оборудованию, что позволяет создавать схемы с высокой выразительностью и малой глубиной. В частности, HEA требует применения последовательных блоков параметризованных вращений одного кубита с общим запутывающим унитарным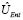 
.
Примером для кубитов N является
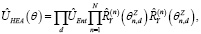
где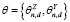 
группирует все вариационные параметры,
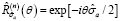
обозначает однокубитный поворот на угол θ вокруг оси
Библиографическая ссылка
Тырышкин С.Ю. ЭФФЕКТИВНЫЕ КВАНТОВЫЕ АЛГОРИТМЫ ДЛЯ КВАНТОВОГО ОПТИМАЛЬНОГО УПРАВЛЕНИЯ // Современные наукоемкие технологии. 2025. № 3. С. 66-72;URL: https://top-technologies.ru/ru/article/view?id=40325 (дата обращения: 04.04.2025).
DOI: https://doi.org/10.17513/snt.40325