Введение
В современных исследованиях газодинамических систем математическое моделирование играет ключевую роль, обеспечивая точное описание и прогнозирование поведения потоков газа в различных условиях. Труба Леонтьева (ТЛ) представляет собой теплообменный аппарат типа «труба в трубе» [1], основанный на принципе газодинамической температурной стратификации, которая позволяет перераспределять энергию между дозвуковым и сверхзвуковым потоками без внешнего теплообмена (рис. 1). Этот процесс критически зависит от геометрии входного сопла, которое определяет параметры потока, такие как число Маха, распределение давления и температуры.
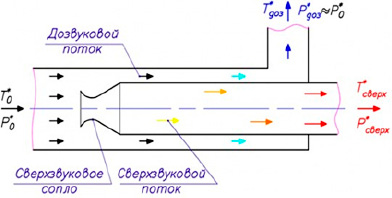
Рис. 1. Схема трубы Леонтьева Источник: составлено авторами по [4]
Несмотря на обширные исследования сопел Лаваля, применяемых для ракетных двигателей и аэродинамических труб [2, 3], их использование в системах с газодинамической стратификацией остается недостаточно исследованным. В частности, до сих пор слабо раскрыты вопросы влияния типа сопла (колоколообразного или кольцевого) на интенсивность псевдошоковых волн, турбулентные потери и устойчивость потока в условиях трубы Леонтьева.
ТЛ эффективно разделяет поток на зоны с пониженной и повышенной температурами, что делает ее полезной для улучшения теплообмена и предотвращения образования гидратов в газопроводах [5]. Кроме того, перспективной областью применения является повышение энергоэффективности и надежности в автомобильных газонаполнительных компрессорных станциях (АГНКС), где оптимальная температура сжатого газа и снижение тепловой нагрузки на оборудование имеют ключевое значение для стабильной и экономичной работы компрессорных агрегатов.
В большинстве работ, таких как исследование O. Dumitrescu с соавторами, фокус сделан на оптимизации сопел для создания тяги или управления двухфазными потоками, при этом игнорируются особенности теплообмена через перегородку в коаксиальных каналах [6]. Например, найдены исследования, посвященные двойным соплам и устойчивости потока в переменных условиях, однако влияние геометрии на температурную стратификацию не рассматривалось [7, 8].
Хотя общие закономерности, влияющие на форму сопла Лаваля (например, углы сужения и расширения), достаточно хорошо описаны в научной литературе, для трубы Леонтьева требуется оптимизация, учитывающая особенности теплообмена через перегородку, а также требуемую разницу температур торможения между каналами [9]. Например, работа по оценке влияния входного стагнационного давления и объемного нагрева на конденсационный водяной пар в сверхзвуковом сопле Лаваля продемонстрировала, что небольшое увеличение входного давления может компенсировать снижение массового расхода при наличии теплового воздействия [10].
В отличие от предыдущих работ, где сопла изучались изолированно [9–11], в данной статье предложена интегральная модель, учитывающая взаимодействие газодинамических и тепловых процессов в коаксиальных каналах.
В одной из работ численно анализировались потоки в соплах с использованием модели k–ε, но без сравнения с k−ω SST (Shear Stress Transport), которая более точно описывает пристеночные турбулентные эффекты [12]. Это создает пробел в понимании оптимальной конфигурации сопла для систем с ограниченным пространством и высокими требованиями к стабильности потока.
Кроме того, найдены работы, где исследуется влияние длины сопла на эффективность разделения энергии в ТЛ с использованием газа с низким числом Прандтля. Установлено, что увеличение длины сопла улучшает разделение энергии, это делает систему более эффективной для использования в теплообменниках [13].
Другое исследование акцентирует внимание на диссипативных эффектах, которые играют важную роль в температурной стратификации [14]. В данной работе рассматривается влияние этих эффектов на изменение температуры в газовых потоках, что напрямую воздействует на эффективность теплообмена в трубах Леонтьева. В частности, исследуется, как трение и другие потери энергии изменяют структуру температурной стратификации и общий теплообмен в системах.
Исследования показали, что геометрия и расположение сопел существенно воздействуют на эффективность охлаждения газовыми струями [15]. В частности, выявлены различия в теплоотведении в зависимости от типа сопел, а также расстояния между соплом и охлаждаемой поверхностью, что напрямую влияет на тепловую эффективность и распределение температуры.
Сопла Лаваля являются ключевыми элементами для формирования сверхзвуковых потоков, преобразующих потенциальную энергию тепла и давления газа в кинетическую энергию (рис. 2). Эта способность делает их незаменимыми в инженерных системах, таких как ракетные двигатели, гиперзвуковые испытательные камеры и системы теплообмена.
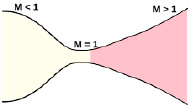
Рис. 2. Схема сопла Лаваля Источник: составлено авторами по [16]
Основной принцип работы сопла Лаваля заключается в последовательном изменении площади поперечного сечения канала. Сужающаяся часть сопла (конвергентный участок) ускоряет поток газа в дозвуковом режиме, приводя его к звуковой скорости в горловине. После горловины, в дивергентной части сопла, поток продолжает ускоряться, достигая сверхзвуковых скоростей.
Различные исследования подтвердили важность геометрии сопел для достижения оптимальных параметров работы. Основные виды сопел включают:
1) конические сопла с линейной геометрией, которые просты в изготовлении и обеспечивают стабильные потоки;
2) колоколообразные сопла, которые имеют классическую сходящуюся-расходящуюся форму; их плавные контуры минимизируют турбулентность и потери энергии. Сопла данной конфигурации являются темой данного исследования;
3) кольцевые сопла, используются для управления потоком в сложных условиях, обеспечивая высокую точность регулирования параметров.
Каждый тип имеет свои преимущества в зависимости от приложения. Например, конические сопла подходят для простых систем, тогда как колоколообразные используются в высокоточных инженерных задачах [17].
Цель исследования: провести сравнительный анализ колоколообразных и кольцевых сопел Лаваля, применяемых в трубе Леонтьева, и определить влияние их геометрии на распределение давления, скорости и температуры в дозвуковом и сверхзвуковом потоках для обоснования оптимальных параметров, повышающих эффективность газодинамической стратификации.
Материалы и методы исследования
В рамках данного исследования для численного анализа газодинамических процессов в трубе Леонтьева применен программный комплекс ANSYS Fluent, который решает систему уравнений Навье–Стокса, описывающих движение вязкого сжимаемого газа. Данный подход основан на фундаментальных уравнениях сохранения массы, импульса и энергии, а также уравнении состояния рабочего тела, что позволяет точно моделировать поведение сверхзвуковых и дозвуковых потоков в сложных геометрических конфигурациях.
Уравнение сохранения массы (неразрывности):
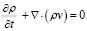, (1)
где ρ – плотность газа, v – вектор скорости.
Уравнение сохранения импульса (Навье–Стокса):
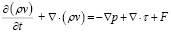, (2)
где p – давление, τ – тензор вязких напряжений, F – внешние силы.
Уравнение энергии:
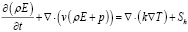,(3)
где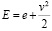 
– полная энергия, k – коэффициент теплопроводности, T – температура, Sh – источник тепла.
Уравнение состояния идеального газа:
p = ρRT, (4)
где R – удельная газовая постоянная.
Для учета турбулентных эффектов применена модель турбулентности k−ω SST, которая описывается следующими уравнениями:
Уравнение для кинетической энергии турбулентности k:
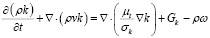, (5)
где Gk – генерация турбулентной кинетической энергии, μt – турбулентная вязкость, σk – коэффициент Прандтля для k.
Уравнение для удельной скорости диссипации турбулентной энергии ω:
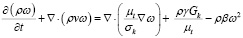, (6)
где γ и β – эмпирические константы модели, μt – турбулентная вязкость, σk – коэффициент Прандтля для ω.
Граничные условия для моделирования включают задание полного давления и температуры на входе сопла, статического давления на выходе, а также условия прилипания и адиабатичности на стенках. Эти граничные условия отражают реальные эксплуатационные параметры системы и обеспечивают устойчивость численных расчетов.
Расчеты выполнялись в стационарной постановке с использованием схемы второго порядка точности. Для турбулентного течения была выбрана модель k−ω SST, наиболее подходящая в областях с интенсивными градиентами скорости. Плотность газа рассчитывали с использованием модели идеального газа.
Расчетная область была разделена на несколько зон:
1) зону с наиболее плотной сеткой вдоль стенок внутреннего канала, где происходит теплообмен;
2) зону вдоль оси внутреннего канала и центральной части окружности кольцевого канала, где наблюдаются наибольшие значения скорости и температуры;
3) зону с менее плотной сеткой в оставшейся части области.
Базовый размер ячеек составлял 0,001 м. При увеличении размера сетки наблюдалось снижение точности расчетов, а при уменьшении – значительный рост временных затрат. Установленный базовый размер был признан оптимальным с точки зрения точности и вычислительных ресурсов.
На входе в расчетную область задавалось полное давление Ptotal = 280 000 Па и начальное избыточное давление Psupersonic = 200 000 Па, что соответствует условиям, близким к реальным эксплуатационным параметрам для обеспечения устойчивого течения в каналах. На выходе задавалось избыточное давление Pgauge = 50 000 Па.
Расчеты проводили до достижения остаточных невязок на уровне 10−6. Особое внимание было уделено анализу скорости сходимости для различных конфигураций сетки и параметров модели.
Результаты исследования и их обсуждение
В рамках численного анализа выполнено моделирование двух типов сопел Лаваля: колоколообразного и конического. Для каждой конфигурации проведен анализ распределения температуры, скорости и давления потока газа.
На рисунке 3 показано распределение температуры.
Колоколообразное сопло (слева) характеризуется плавным изменением температуры, тогда как в кольцевом сопле (справа) температура газа в кольцевом канале значительно повышается, этот эффект обусловлен переходом сверхзвукового потока в дозвуковой через псевдошоковые волны (рис. 4).
На рисунке 5 представлено распределение давления. В кольцевом сопле наблюдаются резкие перепады давления в дивергентной части, связанные с переходом через псевдошоковые волны. В колоколообразном сопле давление изменяется более плавно, что снижает вероятность образования ударных волн.
На рисунке 6 представлено распределение температуры и давления вдоль сопел.
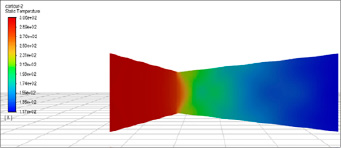
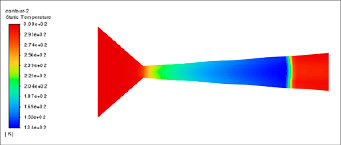
Рис. 3. Сцены распределения температуры Источник: составлено авторами
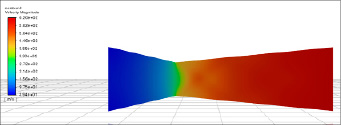
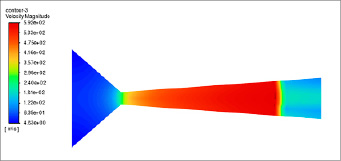
Рис. 4. Сцены распределения скорости Источник: составлено авторами
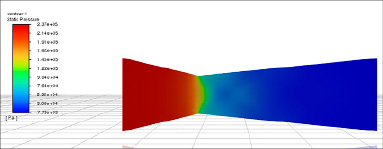
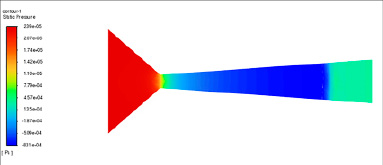
Рис. 5. Сцены распределения давления (составлено авторами)
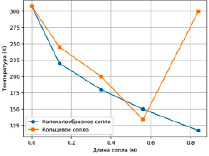
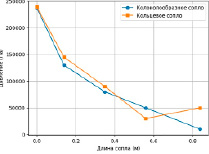
Рис. 6. Сцены распределения температуры и давления вдоль сопел Источник: составлено авторами
Колоколообразное сопло демонстрирует плавное уменьшение температуры от входа к выходу, достигая минимального значения 117 К. В кольцевом сопле наблюдается аналогичное снижение температуры, однако в конце отмечается ее повышение до 300 К, что связано с особенностями аэродинамики данного типа сопла. В то же время давление в колоколообразном сопле плавно снижается от 237 000 Па на входе до 10 000 Па на выходе. В кольцевом сопле после снижения до 30 000 Па в сужающейся части давление увеличивается до 50 000 Па перед выходом, что связано с формированием псевдошоковой волны.
На рисунке 7 представлено распределение скорости вдоль сопел.
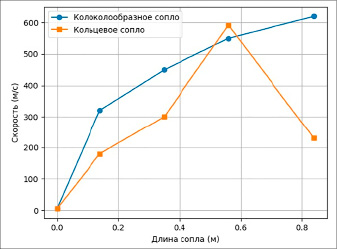
Рис. 7. Распределение скорости вдоль сопел Источник: составлено авторами
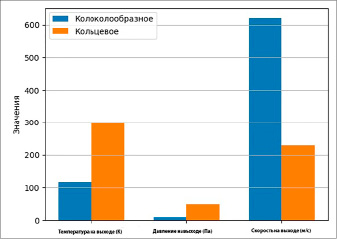
Рис. 8. Сравнение параметров на выходе сопел Источник: составлено авторами
Колоколообразное сопло демонстрирует устойчивое увеличение скорости до 620 м/с на выходе. В кольцевом сопле скорость также возрастает, но в финальной четверти наблюдается ее снижение до 230 м/с, что связано с перераспределением энергии потока. На рисунке 8 приведено сравнение параметров на выходе сопел.
Колоколообразное сопло обеспечивает более низкую температуру и давление, но максимальную скорость. Кольцевое сопло отличается повышенными значениями температуры и давления, но меньшей скоростью на выходе.
Основные достоинства и недостатки представленных сопел в таблице.
Достоинства и недостатки каждой конфигурации сопла
|
Конфигурация сопла |
Достоинства |
Недостатки |
|
Колоколообразное сопло |
Плавное изменение параметров потока снижает вероятность образования ударных волн |
Более сложная конструкция, что может увеличивать затраты на производство |
|
Высокая стабильность потока и минимальные потери энергии |
Меньшая интенсивность перераспределения энергии в условиях высоких нагрузок |
|
|
Обеспечивает лучшее перераспределение энергии между дозвуковым и сверхзвуковым потоками |
||
|
Коническое сопло |
Простая геометрия, что снижает производственные издержки |
Резкие градиенты давления и температуры создают турбулентные зоны |
|
Более высокая интенсивность перераспределения энергии |
Имеется вероятность формирования псевдошоковых волн, снижающих эффективность |
Примечание: составлено авторами на основе численного моделирования в ANSYS Fluent.
Для верификации численной модели входного сопла – критически важного элемента трубы Леонтьева – результаты моделирования были сопоставлены с экспериментальными данными из работы Dumitrescu с соавторами, где проводились испытания сопла Лаваля с холодным газом [18]. Сравнение показало, что численное значение давления на выходе колоколообразного сопла (10 000 Па) отклоняется от экспериментального значения (примерно 15 000 Па) менее чем на 33%, что в контексте сложной геометрии и турбулентных эффектов считается приемлемым. Распределение скорости (620 м/с) также находится в пределах экспериментального диапазона (300–600 м/с) с отклонением около 3%, что подтверждает надежность модели k-ω Shear Stress Transport (SST) для описания сверхзвуковых потоков в условиях исследования.
Результаты моделирования подтверждают и дополняют данные литературы, показывая, что колоколообразные сопла Лаваля обеспечивают стабильное перераспределение энергии между дозвуковым и сверхзвуковым потоками, снижая турбулентные потери и повышая эффективность системы. Конические сопла, напротив, усиливают локальное перераспределение энергии, но при этом отмечен рост турбулентных эффектов и псевдошоковых волн, что снижает их эффективность [19].
Новизна исследования заключается в анализе колоколообразных и кольцевых сопел в контексте трубы Леонтьева, что позволило выявить специфические закономерности, такие как влияние геометрии сопла на псевдошоковые волны, и их связь с температурной стратификацией.
Заключение
Использование колоколообразных сопел в конструкции трубы Леонтьева позволяет повысить эффективность устройства за счет минимизации турбулентных потерь и обеспечения стабильной работы системы. Конические сопла, несмотря на их простоту, лучше подходят для задач, где требуется интенсивное перераспределение энергии, но их применение ограничено высокими потерями энергии и сниженной устойчивостью процессов.
В перспективе полученные результаты могут найти применение при совершенствовании автомобильных газонаполнительных компрессорных станций, где рациональное распределение тепловой энергии в процессе сжатия служит одним из ключевых условий надежной и экономичной работы компрессоров.
Библиографическая ссылка
Ковальногов В.Н., Рудник Р.С., Матвеев А.Ф., Азылов Т.З. ОПТИМИЗАЦИЯ ГЕОМЕТРИИ ВХОДНОГО СОПЛА ДЛЯ УВЕЛИЧЕНИЯ ЭФФЕКТИВНОСТИ ГАЗОДИНАМИЧЕСКОЙ СТРАТИФИКАЦИИ В ТРУБЕ ЛЕОНТЬЕВА // Современные наукоемкие технологии. 2025. № 3. С. 31-39;URL: https://top-technologies.ru/ru/article/view?id=40320 (дата обращения: 04.04.2025).
DOI: https://doi.org/10.17513/snt.40320