Введение
В настоящее время все более актуальной становится концепция интеллектуальных месторождений [1]. Управление программами геолого-технических мероприятий (ГТМ) на скважинах и физико-химических методов воздействия на пласт для повышения нефтеотдачи связано с необходимостью анализа больших объемов постоянно обновляющихся геолого-физических и технологических данных [2]. Сложность и трудоемкость такого анализа делает актуальной разработку высокоэффективных методов и алгоритмов обработки и анализа промысловых данных. С другой стороны, например, управление и планирование ГТМ представляет собой сложную, многопараметрическую задачу. И самыми важными элементами такой задачи являются выбор скважин-кандидатов для ГТМ и определение вида ГТМ для таких скважин [2]. Так, в работе [2] в этом случае использовались глубокие нейронные сети прямого распространения, а в [3] применялся кластерный анализ для анализа скважин и необходимости проведения ГТМ. В работах [4–6] для выбора скважин кандидатов для ГТМ применялся метод нечеткой логики. В работе [7] этот метод использовался для оценки пласта, операций по бурению и заканчиванию скважин, стимуляции притока.
В исследовании [8] представлен инновационный нейросетевой подход для прогнозирования коэффициента нефтеотдачи в условиях полимерного заводнения. В качестве основы для обучения сети была использована функция обратного распространения ошибки, которая интегрировала семь входных параметров для предсказания единственного выходного значения. Архитектура сети включала скрытый слой из 12 нейронов. Для валидации модели были привлечены независимые экспериментальные данные, подтвердившие ее точность и надежность.
В работах [9, 10] предложена многоаспектная методика оценки эффективности геолого-технических мероприятий, сочетающая в себе статистические методы и алгоритмы машинного обучения. Данная методика позволяет прогнозировать ключевые показатели, такие как прирост дебита жидкости и нефти, объем дополнительной добычи, динамику изменения пластового давления, а также темпы обводнения продукции скважин. Такой комплексный подход обеспечивает более точное планирование и оптимизацию процессов разработки месторождений.
Для управления и прогнозирования разработки месторождений используется также прокси-моделирование [11–13]. Для скважинных процессов прокси-модель применялась, например, в [14]. Прокси-модель представляет собой упрощенную математическую модель, способную с высокой точностью воспроизводить и прогнозировать ключевые показатели работы скважин, аналогично гидродинамической модели. Однако, в отличие от последней, прокси-модель минимизирует погрешности, поскольку базируется на первичных промысловых данных, что делает ее более адаптивной и менее зависимой от сложных расчетов. Она особенно востребована в случаях, когда объем или качество данных недостаточны для построения полноценной трехмерной гидродинамической модели (ГДМ). Благодаря своей гибкости и скорости расчетов, прокси-модели становятся эффективным инструментом для оперативного анализа и принятия решений в условиях ограниченной информации.
Прокси-модель позволяет проводить расчеты значительно быстрее по сравнению с ГДМ, подходит для оперативного управления разработкой месторождений в реальном времени, не требует детализированных входных данных, быстро адаптируется к изменению режимов работы скважин. Но прокси-модель не учитывает сложные пространственные эффекты и трехмерную геометрию пласта, эффективна только для определенных типов задач (например, оперативное управление), не подходит для долгосрочного прогноза или моделирования сложных сценариев, не способна учесть все тонкости поведения флюидов в пласте, особенно в условиях сильной неоднородности или изменения режима работы месторождения, требует высокой калибровки на основе данных ГДМ или истории эксплуатации, чтобы быть надежной.
Цель исследования – разработать комплексный, нейросетевой и гидродинамического моделирования двухфазной фильтрации метод оптимизации геолого-технологических мероприятий на нефтяных скважинах, проводимых для интенсификации добычи нефти.
Материалы и методы исследования
Для решения оптимизационных задач существуют мощные и современные оптимизаторы Python – Scipy, Optuna, Hyperopt, PySOT. Идея глубокого обучения заключается в обучении искусственной нейронной сети (ИНС) из нескольких слоев в наборе данных. Существует множество библиотек глубокого обучения, таких как TensorFlow, Theano, CNTK, Caffe, Torch, Neon,Pytorch.
В данном случае для обработки таблиц Excel технологических режимов группы скважин месторождения Оренбургской области для определения наиболее эффективных ОПЗ использовался оптимизатор AdamW, библиотеки и модули Python с Min-Max Scaling нормализацией данных.
Рассматривались скважины с историей проведения различных ГТМ: гидравлический разрыв пласта (ГРП), кислотная обработка (СКО), тепловые методы обработки призабойной зоны.
AdamW (Adaptive Moment Estimation with Weight Decay) – это модификация оптимизатора Adam, которая включает в себя регуляризацию весов (weight decay), что делает его эффективным для задач оптимизации, таких как выбор эффективных обработок нефтяных скважин. В данном случае AdamW может быть использована для настройки параметров модели, которая предсказывает эффективность различных технологических обработок на основе технологических характеристик скважин.
После численных экспериментов с варьированием числа слоев и нейронов для решения задачи выбора ГТМ была использована полносвязная нейронная сеть (MLP) с тремя скрытыми слоями и методом Dropout регуляризации данных, предотвращающим переобучение, с вероятностью отключения нейронов 0,3. Архитектура сети включает входной слой с 10 нейронами, 3 скрытых слоя с 32 нейронами в каждом и выходной слой с 3 нейронами (ГРП, СКО, прогрев).
Входные параметры ИНС:
– Температура на забое (°C).
– Давление на забое (МПа).
– Повышение дебита (м³/сут).
– Плотность нефти (кг/м³).
– Вязкость нефти (мПа·с).
– Пористость пласта (%).
– Проницаемость пласта (мД).
– Обводненность скважины (%).
– Глубина скважины (м).
– Тип коллектора.
В качестве активационной функции в скрытых слоях использовалась функция ReLU, а в выходном слое – Softmax. Функция потерь – CrossEntropyLoss, которая широко используется в задачах классификации в машинном обучении, особенно в задачах с несколькими классами. Она измеряет разницу между распределением вероятностей, предсказанным моделью, и истинным распределением (метками классов). Чем меньше значение кросс-энтропийной потери, тем лучше модель предсказывает правильные классы.
Результаты исследования и их обсуждение
Сеть обучалась на данных 500 скважин. На рис. 1 представлены результаты обучения нейросети на обучающей и валидационной выборке.
График потерь показывает уменьшение потерь на обучающей и валидационной выборках. График точности показывает увеличение точности на обеих выборках. Обученная таким образом ИНС позволяет оценить вероятность успешного проведения определенного типа ГТМ для тестовой выборки скважин. Если в качестве тестовой выборки взять данные малодебитных глубоких скважин, разрабатывающих пласт с высоковязкой нефтью, то получим результаты, подобные приведенным в таблице.
Таким образом, выполненная классификация позволяет разработать перспективную программу проведения различных ГТМ на этом наборе скважин.
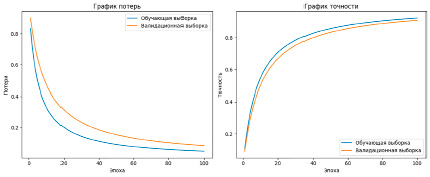
Рис. 1. Графики изменения потерь и точности в задаче выбора типа ГТМ
Результаты выбора ГТМ на тестовых скважинах
|
Образец |
Вероятность успешного применения |
||
|
ГРП |
СКО |
Прогрев |
|
|
1 |
0,3 |
0,2 |
0.5 |
|
2 |
0,2 |
0,2 |
0.6 |
|
3 |
0,1 |
0,3 |
0.6 |
|
4 |
0,5 |
0,1 |
0.4 |
|
5 |
0,3 |
0,3 |
0.6 |
|
6 |
0,2 |
0,3 |
0.5 |
Вместе с тем для реализации сформированной программы потребуется технико-экономическое обоснование предстоящих работ, которое, помимо оценки экономических показателей, включает еще и технологические параметры, выбор оборудования, а также оценку состояния объекта, в том числе пласта.
Такую оценку можно сделать разными способами, с помощью промышленных симуляторов, 3D-гидродинамического моделирования, программных пакетов с открытым исходным кодом, упрощенных математических моделей и т.д. Представляется интересным также использование машинного обучения и при выборе оптимальных параметров ГТМ. Однако использование машинного обучения для определения эффективных параметров ГТМ требует представительной и достоверной информации об опыте применения конкретной технологии. Если такого опыта нет или недостаточно, то возможно использовать результаты расчетов на математических моделях как материал для обучающей и валидационной выборок. Тогда точность определения параметров ГТМ будет зависеть еще и от точности используемых математических моделей. Поскольку одному из авторов приходилось участвовать в нескольких проектах по оптимизации добычи высоковязкой нефти на малодебитных скважинах в Оренбургской области и часть результатов приведена в работах [15, 16], то дальнейшее изложение материала будет основано и на этих материалах тоже. Цели нейросетевой оптимизации на этом этапе: увеличить дебит нефти, снизить время прогрева, снизить температуру на забое, уменьшить вязкость нефти.
Метрики:
1. Дебит нефти, Q1.
2. Время прогрева, Q2.
3. Температура на забое, Q3.
4. Вязкость, Q4.
Веса:
• w1 = 0.4 (важность дебита нефти).
• w2 = 0.3 (важность прогрева).
• w3 = 0.2 (важность температуры.
• w4 = 0.1 (важность вязкости).
Целевая функция:
Целевая функция = w1∙Q1+w2∙Q2+w3∙Q3+w4∙Q4.
Использовалась комбинированная функция потерь с учетом метрик:
Loss = w1∙MSEдебит+w2∙MSEпрогрев+w3∙MSEтемпература+w4∙MSEвязкость,
где MSE – среднеквадратичная ошибка (Mean Squared Error), стандартная функция потерь для задач регрессии. Она измеряет среднее значение квадратов отклонений предсказаний от истинных значений. Архитектура сети представляла собой входной слой с 10 нейронами, 3 скрытых слоя с 64, 32, 32 нейронами с функцией активации ReLU и выходной слой с 4 нейронами без функции активации в соответствии с метриками. Входные параметры ИНС вместо плотности нефти включали время прогрева.
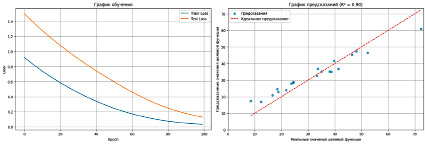
Рис. 2. График обучения и предсказания режимов прогрева
Следует отметить, что входные параметры и метрики – это разные, но взаимосвязанные понятия в контексте ИНС. Входные параметры представляют собой данные, которые подаются на вход модели, а метрики используются для оценки ее производительности. Качество входных параметров напрямую влияет на метрики, поэтому важно тщательно выбирать и анализировать входные данные для достижения высоких результатов. Кроме того, входные параметры используются для гидродинамического моделирования, которое позволяет более детально описать процесс. Результаты обучения на выборке из 100 скважин представлены на рис. 2.
Снижение ошибок на тренировочной и тестовой выборках показывает хорошее обучение нейросети. На графике предсказаний R2-коэффициент детерминации – это статистическая метрика, которая показывает, насколько хорошо модель объясняет вариацию целевой переменной. Другими словами, R² измеряет, насколько хорошо модель предсказывает значения целевой переменной по сравнению с простым средним значением:
- R² = 1, модель идеально объясняет все вариации данных, все точки лежат на линии предсказаний;
- R² = 0, модель не объясняет вариации данных, предсказания модели не лучше, чем простое среднее значение;
- R² < 0, модель работает хуже, чем предсказание средним значением, это может произойти, если модель сильно переобучена или неправильно настроена.
Проверка модели на группе тестовых скважин показала точность определения режимов прогрева и дебита не хуже 21 %.
Как было отмечено, некачественные промысловые данные существенно влияют на возможности и обоснованность результатов нейросетевых алгоритмов. Альтернативой и дополнительным инструментом может служить математическое моделирование.
Цель упрощенного гидродинамического моделирования после выбора эффективного ГТМ заключается в оценке влияния данного мероприятия на производительность скважин и общие показатели разработки месторождения. Это моделирование позволяет решить важные вопросы:
1. Оценить эффективность ГТМ. Определить, насколько выбранное мероприятие улучшает дебит скважин, снижает обводненность.
2. Предсказать, как изменятся показатели добычи (дебит нефти, воды).
3. Оптимизировать разработку. Использовать результаты моделирования для принятия решений о дальнейших действиях, таких как планирование новых ГТМ, корректировка системы заводнения или изменение режимов работы скважин.
4. Снизить риски. Упрощенное моделирование помогает минимизировать неопределенность и риски, связанные с внедрением новых технологий или изменением условий разработки.
В работах [15, 16] одного из авторов данной статьи достаточно подробно проанализированы различные аспекты технологии прогрева нефтяных скважин. Теоретически в рамках моделей однофазной и двухфазной фильтрации пластовых флюидов показаны преимущества и недостатки различных способов прогрева: электронагреватель, нагревательный кабель, ультразвуковой и электромагнитный прогрев призабойной зоны скважины.
Математическая модель процесса прогрева пласта включает уравнения движения и сохранения массы воды и нефти (в двухфазной постановке) [16]. Отличительной особенностью рассматриваемой модели является необходимость учета, в рамках однотемпературной задачи, конвективного и кондуктивного переноса тепла с помощью уравнения энергии:
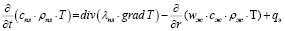 ,
,
где λпл – эффективный коэффициент теплопроводности пласта (порода + флюид);
λск – коэффициент теплопроводности горной породы;
w – скорость фильтрации флюида;
сж, спл – удельная массовая теплоемкость флюида и пласта (жидкость и порода) соответственно;
ρж, ρпл – плотность флюида и пласта;
Т – температура.
В численных расчетах для оценки влияния температурного фактора на призабойную зону использовались экспериментальные зависимости относительных фазовых проницаемостей от водонасыщенности [16].
Сформулированная задача решалась численно методом конечных элементов. Некоторые практически важные результаты решения представлены на рис. 3–6. Расчеты выполнялись с постоянной температурой на стенке скважины, что имитирует работу электронагревателей различных типов. Обращает на себя внимание зависимость размера зоны прогрева от дебита на скважине.
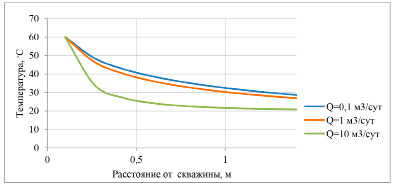
Рис. 3. Распределение температуры в пласте при температуре нагревателя 60ºС
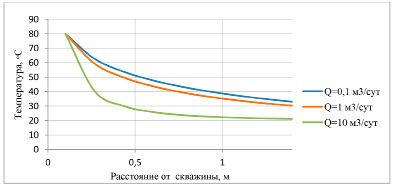
Рис. 4. Распределение температуры в пласте при температуре нагревателя 80ºС
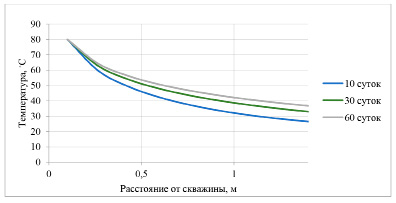
Рис. 5. Распределение температуры в пласте при температуре нагревателя 80ºС (Q = 1 м3/сут)
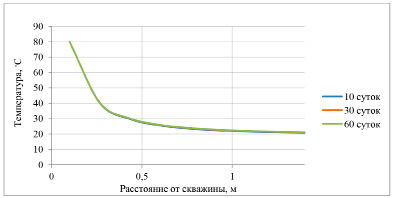
Рис. 6. Распределение температуры в пласте при температуре нагревателя 80ºС (Q = 10 м3/сут)
При дебитах Q больше 10 м3 (рис. 6) зона прогрева вообще не зависит от длительности процесса. В этом случае конвективный перенос тепла от холодного флюида к скважине превышает кондуктивный в пласт от нагревателя.
Именно этим объясняется малая зона прогрева при использовании электронагревателей на малодебитных скважинах. Что, впрочем, не исключает их применения для растворения парафинов и декольматации в узкой прискважинной зоне. Расчетами показано, что применение электронагревателей может повысить дебит низкодебитной скважины максимум в 1,5 раза за счет снижения вязкости нефти. На нейросетевой модели, построенной на промысловых данных, максимальное повышение дебита при температуре 80ºС в 1,2 раза. Отличие результатов по математической модели и полученных в ИНС можно объяснить тем, что в математическую модель закладываются исходные «идеальные» начальные данные, которые, как известно, существенно меняются в процессе эксплуатации скважины.
Заключение
В рамках совместного применения методов машинного обучения и гидродинамического моделирования показана возможность планирования ГТМ на нефтяных скважинах. С помощью нейросетевой оптимизации, на базе данных технологических режимов скважин с историей проведения различных ГТМ разработан алгоритм классификации скважин по эффективным ГТМ. Приведена возможная архитектура ИНС для оптимизации режимов прогрева низкодебитных скважин, что представляет особую значимость для разработки месторождений с высоковязкой нефтью. В отличие от традиционных подходов, представленных в большинстве научных работ, в данной статье предложен комплексный метод, сочетающий в себе алгоритмы глубокого машинного обучения и математическое моделирование двухфазной фильтрации в призабойной области. Такой подход позволяет не только учесть сложные физико-химические процессы, происходящие в пласте, но и существенно повысить точность прогнозирования результатов теплового воздействия.
В ходе численного моделирования получены пространственные распределения ключевых характеристик пласта, таких как температура, вязкость флюида и их влияние на эффективность добычи. Результаты расчетов подтвердили, что предложенная методика позволяет лучше прогнозировать извлечения нефти, особенно в условиях высокой вязкости и низкой проницаемости пласта.
Библиографическая ссылка
Тютяев А.В., Кадет В.В., Васильев И.В., Павлов А.Е., Макаров И.Ю., Макаров Д.Ю. НЕЙРОСЕТЕВОЕ ПРОКСИ-МОДЕЛИРОВАНИЕ ПРОГРАММ ТЕХНОЛОГИЧЕСКИХ МЕРОПРИЯТИЙ НА НЕФТЯНЫХ СКВАЖИНАХ // Современные наукоемкие технологии. 2025. № 2. С. 65-72;URL: https://top-technologies.ru/ru/article/view?id=40305 (дата обращения: 28.12.2025).
DOI: https://doi.org/10.17513/snt.40305



