Введение
На протяжении последних нескольких лет поддерживать темпы выполнения закона Мура становится сложной и отнюдь не тривиальной задачей. Отдавая должное различным инновациям, которые уже сегодня позволяют удовлетворить высокие требования к мощности и производительности экзамасштабных систем, в научно-экспертном сообещстве прогнозируется, что альтернативный подход даст возможность обеспечить устойчивый рост вычислительной мощности за пределами экзамасштаба. По мнению исследователей, одной из таких альтернатив являются квантовые вычисления (КВ), которые обладают потенциалом экспоненциального ускорения для некоторых типов вычислений [1]. В этой ситуации, несомненно, доминирует цифровая модель КВ, основанная на вентилях, и, хотя существуют теоретические гарантии того, что другие конкурирующие режимы, например адиабатические КВ, не менее эффективны, они остаются гораздо более нишевой технологией.
Следует отметить, что КВ – это в большей степени комплексный термин, который охватывает ряд различных архитектурных, логических и вычислительных подходов для решения некоторых типов задач, которые классически неразрешимы. Среди широкого спектра приложений КВ классическое моделирование необходимо исследователям в целях разработки оптимизированных квантовых алгоритмов, проверки функциональности квантовых схем и более четкого понимания квантовых операций [2]. В то же время следует отметить, что моделирование квантовых схем – это достаточно сложная и трудновыполнимая задача, поскольку предполагает необходимость проведения больших вычислений, требует наличия значительных объемов памяти для оценки амплитуд состояний кубитов. Например, чтобы реализовать полное моделирование n-кубитной схемы, требуется экспоненциальный размер вектора для хранения 2n амплитуд [3]. Для решения данной проблемы ученые активно изучают сжатие данных, рассматривают возможности оптимизации схем и перспективы проведения параллельных вычислений.
В данном контексте особого внимания заслуживает симулятор квантовых схем на основе вектора состояния, который эффективно поддерживает инкрементальность с помощью параллелизма задач. Параллелизм данных хорошо работает для высокорегулярных вычислений, которые можно представить как операции над плотными матрицами. Центральным моментом данного предложения является разделение квантовой системы на ряд подэлементов, которые слабо запутаны и могут моделироваться параллельно на разных схемах. Влияние различных областей системы друг на друга можно суммировать эффективным состоянием на гораздо меньшем количестве квантовых битов. Кроме того, параллелизм данных позволяет разделить вычислительные задачи и данные на невзаимодействующие подмножества, что значительно снижает накладные расходы на взаимодействие с внешним окружением. Но в то же время, к примеру, параллелизм с трудом справляется с нерегулярными вычислениями, где объем работы может варьировать между различными «итерациями», подлежащими распараллеливанию.
В связи с этим дальнейшие исследования стратегий параллельного моделирования квантовых схем и перспектив их расширения на квантовые процессоры составляют важную научно-практическую задачу, которая и предопределила выбор темы данной статьи.
Один из первых примеров параллельного симулятора в научной литературе представлен в работах Francisco Pasadas и Pedro C. Feijoo [4]. Он был реализован на языке C и давал возможность провести распараллеливание с помощью интерфейса передачи сообщений. Отличительной характеристикой данного симулятора является использование терминов экспериментальных параметров затвора для реализации квантовых затворов с целью имитации лазерных импульсов в ионных ловушках.
Ряд наработок, касающихся создания инструментальной цепочки для симулятора, которая дает возможность выполнять синтезированные квантовые схемы и запускать открытый стандартный квантовый ассемблерный код, а также проводить сверхглубокие и крупномасштабные симуляции, представлен в трудах Sukin Sim, Peter D. Johnson, Alán Aspuru-Guzik [5]. Стоит также упомянуть работы, где описывались специализированные симуляторы, среди которых выделяются те, которые основаны на тензорных сетях, такие как ExaTN, QTensor и ITensor [6, 7].
Вопросы, связанные с возможностями параллельного выполнения во многих потоках КВ на основе графических процессоров (GPU), а также ключевые аспекты новой методологии программирования для нескольких GPU под названием MG-BSP, которая строит виртуальную BSP-машину поверх современных платформ, рассматривают Bakr Ahmed Taha, Ali J. Addie, Adawiya J. Haider [8].
В то же время при высокой оценке имеющихся на сегодняшний день исследований и наработок некоторые проблемные вопросы, связанные с возможностями параллельных вычислений, остаются открытыми. Так, отдельного внимания заслуживают проблемы с объемом памяти, которые препятствуют расширению моделирования для охвата большего числа кубитов. Помимо этого, влияние квантования с фиксированной точкой на квантовые схемы с увеличивающимся числом кубитов требует дополнительного исследования для всесторонней оценки.
Цель исследования – рассмотреть особенности и перспективы реализации параллельного компактного моделирования квантовых схем.
Материал и методы исследования
Материал и методы исследования – модели, методы, алгоритмы и процедуры параллельного синтеза и анализа специализированных логических схем, численные методы решения алгебраических уравнений, группировка, сравнение, абстракция, дедукция.
Результаты исследования и их обсуждение
Одной из первых работ в направлении параллельного квантового моделирования является параллельная квантовая схема O(log n)-глубины Клива и Уотруса для n-кубитного квантового преобразования Фурье, которая может быть использована для распараллеливания алгоритма факторизации Шора с поливременной классической предварительной и последующей обработкой [9]. Кроме того, учеными был предложен квантовый алгоритм с постоянной квантовой глубиной, который позволяет провести оценку многомерных следов. В то же время следует отметить, что изыскания в направлении параллельных квантовых вычислений не ограничиваются только схемной моделью. Например, в квантовых вычислениях, основанных на измерениях, было замечено, что параллелизм способен обеспечить больше преимуществ, чем в модели схемы. Другой параллельной моделью, которая представляется более близкой к современному квантовому оборудованию, являются распределенные КВ, которые имеют все возможности эффективно моделировать квантовую схемную модель с низкой глубиной накладных расходов [10]. Параллелизм также изучается на более абстрактных уровнях, таких как квантовое программирование.
Параллелизация
Определим параллельное квантовое прохождение, которое может быть реализовано квантовой схемой постоянной глубины с запросами к равномерно структурированным гамильтонианам. Пусть j ∈ Hr, если в графе H существует путь j = (j0, ..., jr)12 длины r + 1.
Предположим, что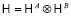 
– пространство состояний, где
.
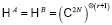Для каждого j0 ∈ [N] определим:
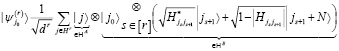(1)
где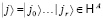 
.
Пусть:
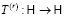любой унитарный оператор, такой, что:
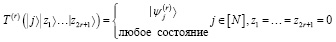(2)
для всех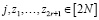 
.
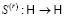оператор обратного порядка:
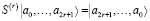(3)
для всех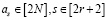 
.
В данном случае шаг r-параллельного квантового прохода для H вычисляется следующим образом: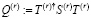 
.
Ключевая идея параллельного квантового прохождения заключается в том, что происходит расширение состояния |Ψj⟩, которое является суперпозицией одного шага движения (j, k) ∈ H, до состояния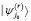 
, которое представляет собой суперпозицию r шагов движения (т.е. пути) j ∈ Hr. Оператор движения Q(r) становится блок-кодом монома (H/d)r, обобщением H/d, полученного из исходного квантового движения. В этом смысле оператор движения Q(r) является расширением T†QT вместо Q. Следует подчеркнуть, что r-параллельное квантовое прохождение не эквивалентно r последовательным шагам исходного квантового прохода, который вместо этого кодирует полином Чебышева Tr(H/d).
Набор квантовых ворот, находящихся на одном уровне, создает унитарную матрицу преобразования, которая определяется произведением Кронекера (⊗) отдельных матриц ворот от первого кубита до n-го кубита [6]. На рисунке 1 показана пятикубитная схема с пятью воротами Хадамарда и четырьмя воротами CNOT.
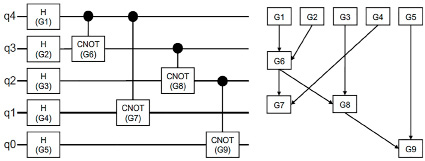
Рис. 1. Пятиквантовая квантовая схема из девяти ворот (слева) и ее граф зависимости от ворот (справа) [6]
Первые пять хадамардовских ворот создают матрицу преобразования 32×32, H⊗5, что позволяет получить суперпозицию. Ворота CNOT формируют запутанность. Поиск унитарных матриц является обязательным элементом моделирования квантовых схем. Вначале осуществляется упорядочивание ворот слева направо и заполняется пустое место матрицей тождества соответствующей размерности. В свою очередь, параллельные ворота могут быть упорядочены произвольно, например G7 и G8.
Общие вычислительные аспекты параллелизации
Время процессора и имеющиеся объемы памяти формируют комплекс ограничений на размер квантового компьютера, который может быть смоделирован на обычном цифровом компьютере. Необходимое время процессора определяется числом операций, которые требуется реализовать с кубитами. Состояние L-кубитного квантового компьютера служит комплексно-значимым вектором длины D=2L. Принимая во внимание потенциально большое количество арифметических операций, которые необходимо осуществить, целесообразно использовать 13–15-разрядную арифметику с плавающей точкой (что соответствует 8 байтам для вещественного числа) [7]. Таким образом, для представления состояния квантовой системы из L кубитов в обычном цифровом компьютере потребуется не менее 2L+4 байт. Следовательно, объем памяти, который требуется для создания модели квантового компьютера с L кубитами, возрастает экспоненциальными темпами с числом кубитов L. Например, для L=24 потребуется не менее 256 МБ памяти для хранения одного произвольного состояния |Ф⟩.
Операции U над вектором состояния |Ф⟩ приводят к преобразованию амплитуд базисных состояний в |Ф⟩. Более конкретно это может быть представлено следующим образом [7]:
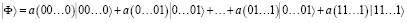(4)
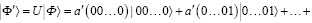
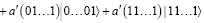(5)
Рассмотрим более подробно одноквантовые операции на кубите j, которые преобразуют |Ф⟩ в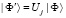 
. Операция Хадамарда на кубите j, Hj преобразует амплитуды в соответствии с:
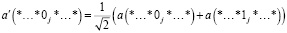(6)
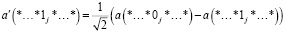(7)
В формулах 6, 7 звездочка обозначает, что биты в соответствующих позициях одинаковы. Для Xj, действующего на |Ф⟩, элементы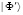 
получаются следующим образом:
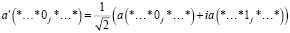(8)
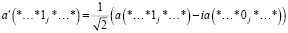(9)
В случае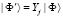 
следует, что:
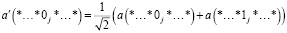(10)
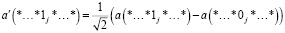(11)
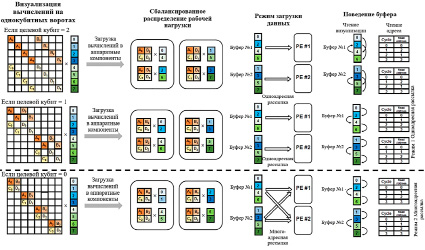
Рис. 2. Два режима (одноадресный и многоадресный режимы загрузки данных) для поддержания баланса рабочей нагрузки
В целом, можно отметить, что выполнение операции над кубитом j требует обновления 2L элементов |Ф⟩. Исключение составляет операция сдвига фазы на одном кубите, которая требует обновления только 2L-1 единичных амплитуд. Необходимо сделать акцент на том, что все эти операции могут быть выполнены на месте, то есть без использования другого вектора длины 2L.
Компактный формат вычислений
При использовании описания вектора состояний применение ворот U к состоянию |ψ⟩ позволяет без излишних затрат и с допустимой скоростью выполнить матрично-векторное умножение U|ψ⟩. Например, применение однокубитных ворот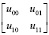 
к состоянию 
дает состояние:
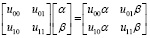(12)
Далее можно распространить (12) на многоквантовые случаи, в результате получаем матрично-векторное представление, которое отображено в левой части на рисунке 2 (применение одноквантовых ворот к трехквантовому вектору состояний с различными целевыми кубитами).
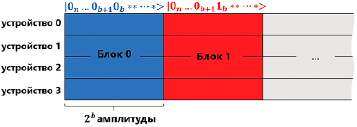
Рис. 3. Схема параллельной компоновка хранилища
Целевой кубит в квантовых воротах отражает запутанность между элементами внутри вектора состояния. Учитывая, что большинство квантовых ворот в обычных схемах являются однокубитными, то есть между большинством элементов нет запутывания, соответствующее матричное представление имеет большое количество нулевых элементов. Для повышения эффективности представляется целесообразным хранить и вычислять только ненулевые элементы, что является, по сути, компактным форматом вычислений.
Направления оптимизации параллелизма для ускорения компактного моделирования квантовых схем
Параллелизм ввода-вывода. Для повышения производительности ввода-вывода эффективным методом может быть организация устройств хранения данных аналогично конфигурации RAID-0, но с большим размером блока (stripe) (рис. 3). При наличии d устройств хранения с параметром размера блока b каждый блок из 2b амплитуд может быть распределен между d устройствами. Каждое устройство содержит 2b/d амплитуд на блок. После этого алгоритм, используя эту схему и библиотеку асинхронного ввода-вывода, распараллеливает операции ввода-вывода.
Размер любой операции ввода-вывода больше или равен 2
Библиографическая ссылка
Тырышкин С.Ю. ПАРАЛЛЕЛЬНОЕ КОМПАКТНОЕ МОДЕЛИРОВАНИЕ КВАНТОВЫХ СХЕМ // Современные наукоемкие технологии. – 2025. – № 1. – С. 185-191;URL: https://top-technologies.ru/ru/article/view?id=40296 (дата обращения: 23.02.2025).