Введение
Структура параллельного сумматора двоичных чисел совершенствуется с каждым новым поколением вычислительных систем. Сумматор – узловой элемент арифметико-логического устройства, от устройства и технологических параметров которого зависят оценки быстродействия, надежности и точности вычислений компьютера в целом. Структуры, особенности функционирования, технологические параметры активно исследуются и обновляются с учетом новых технологий. Результаты исследований отражаются в интенсивном потоке публикаций. Так, основополагающие понятия и алгоритмические конструкции, комплексные подходы в актуальных аспектах проблемы построения параллельных сумматоров освещаются в [1, с. 294; 2, с. 39]. Направления исследований, опирающиеся на преобразования булевых формул и функций, представлены в [3, 4]. Аналогичные направления представлены также в [5, 6]. В целом, разнообразие направлений, в том числе с применением параллельных алгоритмов Когге–Стоуна, первоначально предложенных для преобразования в параллельную форму рекуррентных вычислительных алгоритмов, отражается в [3, 7]. Помимо того, к данному направлению примыкают работы [8, 9]. В рассматриваемом аспекте можно дополнительно указать [10, 11]. На основе булевых формул и функций построены также исследования [12, 13]. Наряду с тем в современных исследованиях структур параллельных сумматоров поддерживаются традиционные направления, опирающиеся на преобразования схемы Склянского. Теоретические результаты фундаментального характера излагаются в [14, с. 10; 15, с. 3], там же освещаются аспекты теории сложности. Направление, связанное с исследованиями Склянского, Когге–Стоуна, Ладнера и других, наиболее соответствует структурам параллельно-префиксных сумматоров. Известные оценки временной сложности параллельного сложения двоичных полиномов имеют вид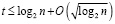 
[16] и 
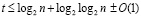, кроме того, указывается оценка 
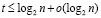, сумматоры имеют линейную сложность по числу элементов [4]. В перечисленных работах порядок временной сложности не улучшается вследствие логарифмической нижней оценки глубины схем переноса [15, с. 4]. В излагаемой ниже работе обсуждается возможность выполнения многоразрядных арифметических операций без вычисления переноса, что позволяет их реализовать синхронно и параллельно по всем разрядам операндов. В основе построения предлагаемой структуры параллельного сумматора лежит выполнение предварительного шага параллельного по всем разрядам сложения битовых коэффициентов равного веса двух двоичных полиномов. Предварительный шаг и последующие преобразования используют арифметические свойства сложения и позиционной двоичной системы счисления. Булевы формулы и функции используются для организации логических элементов, каждый из которых сопоставлен отдельному разряду слагаемых. При данном подходе оказывается возможным исключить логарифмическую глубину схемы переноса. Как результат, достигается единичное время сложения n+1-разрядных двоичных полиномов при произвольном n с линейным количеством элементов сумматора, t(n) = O(1). В данной работе также ставится вопрос о распространении предложенного метода на другие позиционные системы счисления, показано, что искомая возможность реализуется с помощью конструктивных алгоритмов.
Цели исследования. Первой целью является обосновать возможность бинарного сложения n+1-разрядных двоичных полиномов без вычисления переноса с единичной оценкой времени при количестве элементов сумматора, пропорциональном числу разрядов. Вторая цель – рассмотреть аналогичную возможность для произвольной позиционной системы счисления, сравнить предложенный метод с известными аналогами и указать актуальные приложения.
Материалы и методы исследования
Исследование опирается на методы синтеза и анализа параллельных алгоритмов в приложении к разрядному распараллеливанию суммирования двоичных полиномов.
Результаты исследования и их обсуждение
Предложен метод поразрядно-параллельного сложения n-разрядных двоичных полиномов. В максимально параллельной форме сложение выполняется за время O(1) в случае произвольного n. Структура параллельного сумматора отличается от аналогов тем, что не является результатом синтеза схем переноса на основе булевых формул и функций. Предложенный сумматор реализует элементарные операции сложения битовых коэффициентов двоичных полиномов равного веса параллельно по всем разрядам слагаемых. В результате предварительного шага переносы взаимно отделяются промежуточными парами нулевых коэффициентов равного веса, дальнейший процесс реализует физическое разделение цепочек переноса и цепочек единиц без переноса. Разделение реализуется за время однократного переключения элементов. После этого повторяется параллельное по всем разрядам сложение коэффициентов равного веса. Окончательное значение суммы двух двоичных полиномов степени n получается за время O(1) на O(n) разрядных элементах. Известные методы синтеза параллельных сумматоров имеют логарифмическую оценку глубины схемы переноса, время сложения в них оценивается как O(log2n). Сумматор с предложенной структурой позволяет существенно увеличить разрядность данных при выполнении арифметических операций, в результате должна возрасти точность вычислительной обработки. Метод переносится на сложение чисел в произвольной позиционной системе счисления с натуральным основанием.
Исходные соотношения. Описание первого шага поразрядно-параллельного сложения двоичных полиномов. Пусть требуется сложить два n+1-разрядных двоичных полинома с битовыми коэффициентами, что записывается в виде
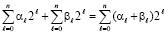, (1)
где
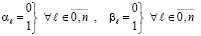. (2)
Сложение коэффициентов равного веса предлагается выполнять по вертикали – синхронно и параллельно по всем разрядам:
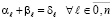, (3)
где
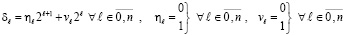. (4)
Ниже параллельное по всем разрядам суммирование вида (3), (4) называется первым шагом вертикального сложения. При выполнении первого шага перенос не распространяется, а результаты параллельного по всем разрядам битового суммирования в виде двухразрядных чисел (4) записываются синхронно и параллельно по всем разрядам согласно весу коэффициентов разрядной суммы – по диагонали. В результате образуется двухрядный двоичный код в двух разрядных сетках (верхней и нижней):
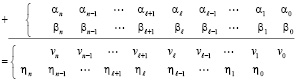(5)
верхняя разрядная сетка
нижняя разрядная сетка
Например,
(6)
В нижней и верхней разрядных сетках суммы (6) последние два разряда результата не отделены вертикальной парой нулей от предшествующих двух переносов. Это происходит в том единственном случае, если эти разряды переноса не содержат. Любой перенос от ближайшего предшествующего, равно как и последующего, переноса необходимо отделять вертикальной парой нулей.
Например,
(7)
Если бы на месте любого нуля разделяющей вертикальной пары нулей в сумме (7) оказалась единица, то это бы означало запись двух единиц по диагонали. Такая запись расшифровывалась бы как сумма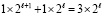 
, тогда как по вертикали складывалось не более двух единиц веса 
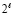. В общем случае два любых переноса, образовавшихся после первого шага вертикального сложения, необходимо отделены друг от друга вертикальной парой нулей. Поэтому после первого шага переносы не накладываются друг на друга: в один и тот же разряд никогда не придут одновременно две единицы. В различной форме эти свойства указывались и использовались в [17, 18]. В дальнейшем алгоритм и реализация суммирования по сравнению с прототипами изменятся.
Имеет место
Лемма 1. Пусть требуется найти сумму двух двоичных полиномов (1), (2). Пусть выполнен первый шаг вертикального сложения (3) – (5) и его результат расположен в верхней и нижней разрядной сетках. Тогда две ближайшие друг к другу цепочки единиц соседней пары переносов в этих двух разрядных сетках необходимо отделяются друг от друга хотя бы одной промежуточной вертикальной парой нулей равного между собой веса (парой нулевых двоичных коэффициентов равного веса в верхней и нижней разрядной сетке). Такая вертикальная пара нулей необходимо располагается в соседнем слева разряде от каждой цепочки переноса, то есть, в разряде на единицу большего веса, чем старший единичный разряд любой цепочки переноса.
Доказательство. По способу выполнения первого шага вертикального сложения, согласно (4), в верхней разрядной сетке суммы (5) оказываются коэффициенты веса, который равен весу битовых коэффициентов слагаемых, взятых по вертикали разряда, и только такие коэффициенты. В нижней разрядной сетке (5) оказываются коэффициенты на единицу большего веса, чем вес коэффициентов по вертикали разряда слагаемых, и только такие коэффициенты. В результате после первого шага вертикального сложения перенос (если он есть) состоит из вертикальной пары единиц равного веса в младшем разряде цепочки, располагающихся в верхней и нижней разрядной сетке и продолжающих их справа налево горизонтальной цепочки единиц без пробелов последующих старших разрядов, располагающейся исключительно в верхней разрядной сетке (5). Под каждым единичным разрядом этой горизонтальной цепочки, за исключением младшего ее разряда, в случае если ее длина больше единицы, находится ноль в нижней разрядной сетке (5). В самом деле, если бы под единицей рассматриваемой горизонтальной цепочки по вертикали в нижней разрядной сетке оказалась бы единица, то это бы означало результат сложения по вертикали трех единичных коэффициентов предшествующего младшего разряда, 
, что невозможно, поскольку по вертикали складываются только два битовых двоичных коэффициента равного веса. Такая горизонтальная цепочка единиц переноса в верхней разрядной сетке своим старшим единичным разрядом необходимо отделяется нулевым значением разряда от ближайшей слева вертикальной пары единиц соседнего переноса в старших разрядах. Если бы она не отделялась нулем и перед левой вертикальной парой единиц справа в верхней разрядной сетке непосредственно находилась бы единица, то это снова бы означало результат суммирования по вертикали трех единиц, на этот раз веса старшего разряда правосторонней цепочки, 
, что по-прежнему невозможно. Где бы относительно ближайшей слева цепочки переноса ни располагался ноль в соседнем с единицей старшем разряде верхней разрядной сетки рассматриваемой правосторонней цепочки переноса, по вертикали от этого нуля, в нижней разрядной сетке должен находиться ноль,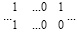 
. Иначе бы вместе с единицей старшего разряда правосторонней цепочки переноса образовался бы результат суммирования трех единиц по вертикали веса этого старшего разряда, 
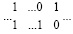, что невозможно. Поэтому непосредственно слева от единицы старшего разряда горизонтальной части цепочки переноса необходимо находится разделительная вертикальная пара нулей веса следующего за этой единицей старшего разряда, 
, причем, какова бы ни была длина горизонтальной цепочки переноса, включая, возможно, единичную длину,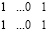 
, – изложенные рассуждения сохраняются в этом случае. Лемма доказана.
Замечание 1. После первого вертикального шага сложения, в отличие от верхней разрядной сетки, в нижней разрядной сетке (5) перед вертикальной парой единиц младшего разряда цепочки переноса справа в соседнем разряде может находиться единица (или подряд несколько единиц). Это возможно только в том случае, когда по вертикали над этой единицей (равно как над единицей младшего разряда подряд несколько таких единиц) и по диагонали от нее в соседнем младшем разряде верхней разрядной сетки находится ноль, 
, как в примерах (6), (7), иначе возникало бы описанное ранее противоречие: 
или 
, что невозможно. На наличие разделительной вертикальной пары нулей двух цепочек переноса рассмотренный в данном замечании случай никак не влияет. Более того, справа рассмотренную и любую другую цепочку единиц (возможно единичной длины) нижней разрядной сетки всегда ограничивает вертикальная пара нулей в силу аналогии с рассуждениями, изложенными непосредственно выше. Кроме того, ни в одном разряде сверху над рассматриваемой цепочкой единиц нижней разрядной сетке нет единиц, то есть сверху над каждой единицей такой цепочки (не входящей в цепочку переноса) всегда расположен ноль верхней разрядной сетки.
Следствие 1. В условиях леммы 1 любая горизонтальная цепочка единиц переноса располагается в верхней разрядной сетке и непосредственно слева ограничена вертикальной парой нулей соседнего с ней старшего разряда, 
, или же она ограничена левым концом верхней разрядной сетки. Справа горизонтальная цепочка единиц переноса ограничена вертикальной парой единиц младшего разряда цепочки и нулем соседнего с вертикальной парой единиц младшего разряда. Такой нулевой коэффициент располагается в верхней разрядной сетке, непосредственно справа от вертикальной пары единиц,
,
или 
.
Или же горизонтальная цепочка единиц переноса ограничена правым концом верхней разрядной сетки.
Для единства терминологии вводится нестандартное для разрядной сетки предположение. Будет предполагаться, что в верхней разрядной сетке после старшего разряда веса 2n, слева от него, располагается еще один разряд, имеющий вес 2n+1, и в этом разряде априори записан 0 (нулевой коэффициент веса 2n+1). Кроме того, будет предполагаться, что в верхней разрядной сетке до младшего разряда веса 20, справа от него, располагается еще один разряд, имеющий вес 0, и в этом разряде априори записано значение 0 (нулевой коэффициент веса 0). Аналогичное предположение вводится относительно нижней разрядной сетки.
В этой терминологии в дальнейшем нет необходимости отдельно оговаривать правые и левые границы горизонтальной части цепочки переноса, если они совпадают с концом или началом разрядной сетки.
Второй шаг поразрядно-параллельной обработки. После первого шага вертикального сложения на втором шаге параллельно выполняется выделение всех горизонтальных цепочек единиц, подряд расположенных в верхней разрядной сетке, которые не являются цепочками переноса. Это делается на той основе, что в ближайшем разряде слева от рассматриваемой цепочки единиц находится разряд с нулевым значением (возможно, это последний справа налево старший разряд веса 2n+1), и в ближайшем разряде справа от этой же цепочки также находится разряд с нулевым значением (возможно, это первый справа налево младший разряд веса 0). При этом непосредственно слева от рассматриваемой цепочки единиц находится не один ноль, а вертикальная пара нулей. Справа от той же цепочки находится не только один ноль, а еще один ноль находится под начальной единицей цепочки. Более точно, имеет место
Лемма 2. Пусть выполнены условия леммы 1. Тогда любая горизонтальная цепочка подряд расположенных в верхней разрядной сетке единиц, не являющаяся цепочкой переноса, ограничена нулями непосредственно слева от старшего и справа от младшего разрядов с единичными значениями. При этом в левую границу входит не один ноль верхней разрядной сетки, а вертикальная пара нулей верхней и нижней разрядной сетки. Кроме того, эта цепочка по определению не включает переноса, и ни под одной ее единицей в верхней разрядной сетке нет единицы того же веса в нижней разрядной сетке. Как следствие ноль справа от рассматриваемой единичной цепочки, расположенный в верхней разрядной сетке, сочетается с нулем по диагонали в нижней разрядной сетке (с нулевым значением под единицей младшего разряда цепочки).
Доказательство. Пусть выполнен первый шаг вертикального сложения. В верхней разрядной сетке горизонтальная цепочка подряд расположенных единиц, не являющаяся цепочкой переноса, не может непосредственно продолжаться влево цепочкой переноса, она отделена, как показано в доказательстве леммы 1, от цепочки переноса хотя бы одним промежуточным разрядом с нулевым значением. При этом ноль левой границы в верхней разрядной сетке входит в вертикальную пару нулей вместе с нулем нижней разрядной сетки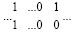 
. Иначе бы вместе с единицей старшего разряда рассматриваемой горизонтальной цепочки образовался бы результат суммирования трех единиц по вертикали веса этого старшего разряда, 
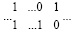, что невозможно. Справа рассматриваемая горизонтальная цепочка единиц верхней разрядной сетки может прерываться только разрядом с нулевым значением, поскольку она начинается с единицы и не включает переноса. Рассматриваемая горизонтальная цепочка единиц верхней разрядной сетки под каждой своей единицей имеет нулевой коэффициент того же веса в нижней разрядной сетке, поскольку, как отмечено, не включает переноса. Ноль в нижней разрядной сетке веса младшего разряда этой цепочки продолжает по диагонали прерывающий цепочку ноль верхней разрядной сетки из соседнего с единицей младшего разряда цепочки, 
. Лемма доказана.
Следствие 2. После первого шага вертикального сложения любая цепочка переноса отличается от любой горизонтальной цепочки единиц, не являющейся цепочкой переноса и расположенной в верхней разрядной сетке, наличием вертикальной пары единиц равного веса в младшем разряде цепочки переноса, а также нулем в верхней разрядной сетке непосредственно справа от вертикальной пары единиц. Ее расположение в верхней и нижней разрядной сетке имеет вид
или 
.
У горизонтальной цепочки единиц, не являющейся цепочкой переноса и расположенной в верхней разрядной сетке, отличительная комбинация двоичных цифр в верхней и нижней разрядной сетке имеет вид:
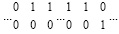
или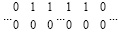 
.
Таким образом, отличительная комбинация трех цифр создается на правой границе рассматриваемой цепочки. Для цепочки переноса с учетом верхней и нижней разрядной сетки отличительная комбинация на правой границе имеет вид: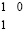 
, а для цепочки единиц, не содержащей переноса, аналогичная комбинация необходимо имеет вид: 
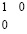. Левые границы рассматриваемых цепочек по виду совпадают и состоят из вертикальной пары нулей перед единицей старшего разряда, эта граничная слева комбинация цифр имеет вид: 
.
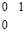Из лемм 1, 2 и из следствий 1, 2 вытекает
Следствие 3. Пусть выполнен первый шаг вертикального сложения. Тогда, чтобы любая горизонтальная цепочка единиц в верхней разрядной сетке не являлась цепочкой переноса, необходимо и достаточно, чтобы непосредственно слева она была ограничена комбинаций цифр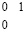 
, где 1 – значение старшего разряда цепочки, и непосредственно справа комбинацией цифр 
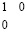, где 1 – значение младшего разряда цепочки.
Граничные комбинации цифр из следствия 3 определяются как соответственно левый и правый идентификаторы горизонтальной цепочки единиц, не являющейся цепочкой переноса.
В примерах (6) и (7) в верхней разрядной сетке нет горизонтальных цепочек единиц, не содержащих переноса. В примере непосредственно ниже в результате выполнения первого шага вертикального сложения такая цепочка содержится в разрядах от веса 24 до веса 27 включительно верхней разрядной сетки (после знака равенства):
(8)
Если каждую полученную после первого шага вертикального сложения горизонтальную цепочку единиц, не содержащую переноса, выделить по левому и правому идентификаторам, а затем параллельно по всем разрядам переписать в нижнюю разрядную сетку с сохранением веса и значений разрядов, то в верхней разрядной сетке останутся только цепочки переноса. Они отделены друг от друга вертикальными парами нулей слева от единицы старшего разряда и ограничены справа вертикальными парами единиц в младших разрядах этих цепочек. Сумма от перезаписи, очевидно, не изменится. Из примера (8) получится:
(9)
Параллельно по всем разрядам такое тождественное преобразование результата первого шага вертикального сложения можно реализовать схемотехнически. Сравнительно несложная схема заключается в следующем. Пусть сумматор располагает двумя условно горизонтально расположенными проводниками электрического тока (шина 1 и шина 2), нижний из которых (шина 2) условно проходит непосредственно над верхней разрядной сеткой (рисунок). По шине 1 непрерывно проходит постоянный ток в направлении справа налево (от младших разрядов к старшим). Обе горизонтальные шины «поразрядно» (по их расположению) соединены вертикальными проводами, в каждый из которых встроено по одному переключателю. Число вертикальных проводных соединений и соответственных им таких переключателей равно числу разрядов верхней разрядной сетки. В вертикальных проводных соединениях переключатели взаимно независимы и работают как «выключатели» – для замыкания и разрыва цепи. При этом они пропускают или запирают ток только в вертикальном направлении сверху вниз. Каждый переключатель (и соответственное ему вертикальное соединение) находится во взаимно однозначном соответствии с разрядом одного и только одного веса (вертикальной пары разрядов) верхней и нижней разрядной сетки. Столько же таких же переключателей тока, но только в горизонтальном направлении, в таком же взаимно однозначном соответствии с разрядами верхней и нижней разрядной сетки, встроено в шину 2. В шине 2 эти переключатели либо проводят ток в направлении от младших разрядов к старшим, либо запирают ток (разрывают цепь). Ток поступает из шины 1 в шину 2 в том и только в том случае, если в соответственное состояние установлен переключатель вертикального соединения, – установка переключателя выполняется через логический элемент управления в соответствии с комбинацией цифр правого идентификатора цепочки единиц, не являющейся цепочкой переноса. Более точно: ток поступает в шину 2 из шины 1 через переключатель вертикального соединения в случае состояния правого идентификатора рассматриваемой цепочки единиц, определяемого комбинацией цифр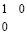 
, где 1 – значение младшего разряда рассматриваемой цепочки. Эта комбинация цифр с помощью логического элемента управления переводит переключатель вертикального соединения, сопоставленный разряду с правой граничной единицей цепочки, в состояние, при котором он направит ток из шины 1 в шину 2. В результате ток пойдет по шине 2 справа налево (в направлении от младших разрядов к старшим). Ток прерывает прохождение по шине 2 в направлении старших разрядов, если в соответственное состояние переводится переключатель шины 2, соответствующий левому идентификатору цепочки единиц, не содержащей переноса. Такое переключение выполняется по управлению от логического элемента, соответственного вертикальной паре нулей в левом идентификаторе рассматриваемой цепочки, имеющем вид: 
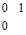, где 1 – значение старшего разряда данной цепочки единиц. Эта комбинация цифр левого идентификатора цепочки переводит переключатель в состояние, при котором он не пропускает ток по шине 2 в направлении старших разрядов дальше вертикальной пары нулей. Одновременно с тем каждая единица рассматриваемой (а также любой другой) горизонтальной цепочки единиц верхней разрядной сетки, непосредственно справа от которой находится единица, по идентификатору 
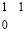посредством управления от логического элемента, сопоставленного разряду данной единицы, отключает сопоставленный ей переключатель вертикального соединения. Точно такое же действие выполняет каждая единица верхней разрядной сетки, если по вертикали под ней находится единица нижней разрядной сетки (вертикальная пара единиц начала цепочки переноса). В это же самое время каждое из всех остальных единичных значений разрядов верхней разрядной сетки через сопоставленный разряду логический элемент ставит сопоставленный этому разряду переключатель шины 2 в априорное состояние, при котором переключатель реализует сквозное прохождение тока по шине 2 справа налево в направлении старших разрядов.
Вся описанная установка состояний вертикальных и горизонтальных переключателей в требуемое положение реализуется синхронно и параллельно по всем сопоставленным переключателям разрядам за один такт непосредственно сразу после выполнения первого шага вертикального сложения – согласно априори полученным на входе второго шага значениям всех разрядов верхней и нижней разрядных сеток.
В результате такой установки состояний контактов всех переключателей ток не будет проходить по шине 2 ни через одну цепочку переноса. Правый идентификатор цепочки переноса имеет вид: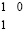 
, поэтому переключатель по вертикали ток в этот разряд не пропускает, а переключатель, соответственный предшествующей справа вертикальной паре нулей младшего разряда, заведомо прерывает прохождение тока справа налево к цепочке единиц переноса. Таким образом, ток не проходит вдоль любой из цепочек переноса, и ни одна из этих цепочек не подвергается никакому изменению.
Напротив, ток проходит по шине 2 вдоль каждой цепочки единиц, не являющейся цепочкой переноса. При этом логический элемент, сопоставленный единице этой цепочки, принимает проходящий по шине 2 ток на свой вход и интерпретирует наличие тока на входе от шины 2 как управляющий сигнал для перезаписи данной единицы из верхней разрядной сетки в нижнюю разрядную сетку с сохранением значения и веса разряда.
Данное преобразование выполняется параллельно по всем разрядам цепочки единиц, не являющейся цепочкой переноса, а также параллельно по всем таким цепочкам, априори взаимно отделенным левым и правым идентификаторами друг от друга (после первого шага вертикального сложения). Все такие цепочки, не являющиеся цепочками переноса, взаимно независимы, обрабатываются синхронно, параллельно, поэтому синхронно и параллельно по всем разрядам перепишутся из верхней разрядной сетки в нижнюю разрядную сетку.
Однако, как отмечалось, ни одна цепочка единиц переноса не подвергнется никакому преобразованию: все единицы всех цепочек переноса останутся на своих местах в верхней разрядной сетке, равно как и ограничивающие их вертикальные пары единиц в младших разрядах верхней и нижней разрядных сеток. Кроме того, без изменения останутся все их граничные идентификаторы.
Описанные соответствия состояний контактов переключателей значениям разрядов слагаемых после первого шага вертикального сложения иллюстрирует рисунок.
Управляющий электрический сигнал на физическое различение цепочек единиц без переноса и с переносом физически направлен (как единичный или соответственно нулевой) от правого идентификатора цепочки. Этот сигнал для каждой цепочки исключается за пределами цепочки, что позволяет выполнить искомые отличительные преобразования одновременно во всех цепочках единиц верхней разрядной сетки и вертикальной пары единиц младшего разряда цепочки переноса.
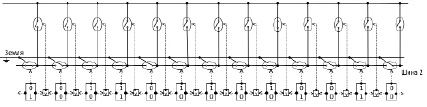
Соответствие состояний контактов переключателей значениям разрядов из (8) Источник: составлено автором
В результате представление слагаемых (8) переводится в форму (9). На этом заканчивается второй шаг поразрядно-параллельной обработки.
Третий шаг поразрядно-параллельной обработки. На выходе преобразований второго шага обработки слагаемых все цепочки единиц из верхней разрядной сетки, не включающие переносы, окажутся в нижней разрядной сетке. Все цепочки единиц верхней разрядной сетки, включающие переносы, останутся без изменений в верхней разрядной сетке. Также без изменений останутся единицы нижней разрядной сетки, входящие в перенос в виде вертикальной пары единиц младшего разряда цепочки переноса или представляющие собой не связанную с переносом цепочку единиц (возможно, единичной длины) нижней разрядной сетки. Третий шаг состоит в следующем преобразовании каждой из цепочек именно переноса. Каждая единица цепочки в верхней разрядной сетке заменяется на минус единицу, записываемую в том же разряде, а чтобы результат сложения арифметически не изменился, к каждой минус единице добавляется плюс два, при этом добавленная двойка записывается согласно весу в соседний старший разряд – по диагонали в нижнюю разрядную сетку. Это равносильно тождеству 1 = –1 + 2, применяемому к каждой единице верхней разрядной сетки. Единицы, поступившие в нижнюю разрядную сетку на выходе первого шага вертикальной обработки, а также на выходе второго шага поразрядно-параллельной обработки, никак не преобразуются. Запись по диагонали добавляемой двойки в виде единицы соседнего старшего разряда в нижнюю разрядную сетку всегда возможна, поскольку согласно следствию 2 по вертикали под каждой единицей верхней разрядной сетки (за исключением вертикальной пары единиц младшего разряда цепочки переноса) находится ноль, а кроме того, ноль находится по диагонали от старшего разряда единицы цепочки переноса. Расположение цепочки переноса в верхней и нижней разрядной сетке имеет вид:
или 
.
В результате запись единиц по диагонали всегда возможна без изменения искомой суммы. Преобразуемые цепочки примут вид:
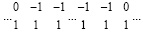
или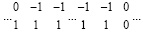 
.
В частности, (9) преобразуется к виду:
(10)
Преобразование выполняется синхронно и параллельно по всем разрядам. В этом состоит третий шаг поразрядно-параллельной обработки.
Четвертый шаг поразрядно-параллельной обработки. Синхронно и параллельно по всем разрядам преобразованного на третьем шаге двухрядного кода промежуточной суммы выполняется вертикальное сложение двоичных коэффициентов равного веса (повторяются действия первого шага вертикального сложения). В результате рассматриваемого вертикального сложения для цепочек переноса сумма примет вид:
,
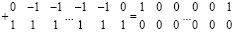или,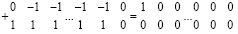 
.
В любом случае под бывшей цепочкой единиц переноса в нижней разрядной сетке будут только нули. В верхней разрядной сетке будет только реализованное по всем разрядам значение переноса.
Для каждой цепочки единиц, не включающей переноса и размещенной в результате третьего шага в нижнюю разрядную сетку, описываемое вертикальное сложение влечет
,
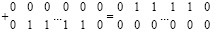то есть такая цепочка без изменения вернется в верхнюю разрядную сетку. Совершенно аналогично в верхнюю разрядную сетку перепишется каждая цепочка единиц, в том числе единичной длины, которая априори (после первого шага вертикального сложения) располагалась в нижней разрядной сетке, будучи никак не связанной с переносом. Таким образом, в верхней разрядной сетке расположится окончательная однорядная сумма двух двоичных полиномов, а нижняя разрядная сетка вся будет заполнена нулями. В частности, для преобразования (10) получится:
(11)
Для полноты обоснования использованной на данном четвертом шаге перезаписи цепочки единиц из нижней разрядной сетки в верхнюю, равно как и предварительной перезаписи цепочки единиц из верхней разрядной сетки в нижнюю, формулируется
Предложение 1. После первого шага вертикального сложения каждая цепочка единиц верхней разрядной сетки, не являющаяся цепочкой переноса, обладает той особенностью, что под каждой единицей этой цепочки по вертикали находится ноль нижней разрядной сетки (нулевой коэффициент того же веса, что и рассматриваемая единица). Одновременно с тем каждая цепочка единиц нижней разрядной сетки обладает той особенностью, что над каждой единицей этой цепочки по вертикали находится ноль верхней разрядной сетки, исключение составляет единица младшего разряда цепочки переноса, если она входит в рассматриваемую цепочку нижней разрядной сетки. После третьего шага поразрядно-параллельной обработки оговорка относительно исключения становится излишней (ввиду априорной реализации каждого переноса).
Доказательство. Если бы на месте нуля по вертикали находилась единица, то она образовывала бы пару вертикальных единиц и перенос, что противоречит условию, с точностью до оговоренного исключения.
На выполнении рассмотренных преобразований завершается четвертый шаг поразрядно-параллельного сложения двоичных полиномов, который является окончательным.
Реализация четвертого шага может быть иной, без ввода отрицательных единиц. Именно: пусть выполнены первый, второй и третий шаги поразрядно-параллельной обработки и все цепочки единиц, не содержащие переноса, переписаны в нижнюю разрядную сетку, а расположение всех цепочек переноса осталось без изменений. Тогда во всех цепочках переноса синхронно и параллельно по всем разрядам выполняется следующее преобразование. Ноль непосредственно слева от единицы старшего разряда цепочки единиц переноса в верхней разрядной сетке инвертируется в единицу. Каждая единица цепочки переноса инвертируется в ноль. В том числе в ноль инвертируется единица из нижней разрядной сетки вертикальной пары единиц младшего разряда цепочки переноса. Таким образом, каждая цифра цепочки переноса, ее левой нулевой границы и вертикальной пары единиц младшего разряда инвертируется в обратный код (инверсия реализуема через функцию логического отрицания). Остальные цифры нижней разрядной сетки не преобразуются. На выходе преобразования реализуется выполнение переноса:
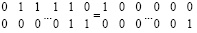, или, 
.
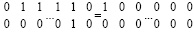Преобразование выполняется синхронно и параллельно по всем цепочкам переноса. Для окончания обработки останется переписать по вертикали с сохранением веса все единицы из нижней разрядной сетки в верхнюю разрядную сетку, где окончательно окажется представленным однорядный код суммы двоичных полиномов. В частности, для преобразования (10) получится:
(12)
Очевидно, (12) эквивалентно (11). На этом завершается данная разновидность четвертого шага поразрядно-параллельного сложения двоичных полиномов.
Оценка временной сложности и числа элементов параллельного сумматора. Передача тока по шине 2 (рисунок) является сквозной – в том смысле, что она происходит при априори зафиксированных состояниях контактов переключательных элементов. Эти состояния зафиксированы синхронно, параллельно по всем разрядам и по всем переключательным элементам, в начале второго шага, сразу после первого шага вертикального сложения, во взаимно однозначном соответствии полученным значениям разрядов. Определяющие состояния контактов переключателей значения разрядов получены на входе второго шага априори, непосредственно с выхода первого шага вертикального сложения, настройка состояний контактов всех переключателей по управлению от разрядных логических элементов выполняется, таким образом, априори. Переключатели не меняют направление тока в процессе выполнения второго шага поразрядно-параллельной обработки, состояние их контактов не зависит от дальнейшего прохождения тока по верхнему и нижнему проводникам, состояние контактов зависит только от априорной параллельной настройки на входе второго шага. Это означает, что ни один из переключательных элементов в процессе выполнения второго шага не перешел из одного состояния в другое, переключатели не подвергались последовательным шагам изменения состояний своих контактов, их состояние стационарно. Состояние контактов переключателей на втором шаге поразрядно-параллельной обработки не вызовет иной задержки времени, кроме той, которая априори потребовалась для однократной параллельной настройки контактов. Поэтому время выполнения второго шага имеет единичную задержку τ, требуемую на переключение логического элемента, затем столько же времени требуется на параллельную перезапись цепочек в нижнюю разрядную сетку. С точностью до постоянного коэффициента такое же время требуется на выполнение первого, третьего и четвертого шагов рассматриваемой поразрядно-параллельной обработки. В результате время рассматриваемого сложения двоичных полиномов формально не зависит от числа разрядов слагаемых (от степени полиномов n) и оценивается как:
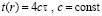, (13)
где константа c зависит от технологических параметров элементов, τ – время однократного переключения элемента. В (13) и ниже r – количество элементов сумматора, которое, очевидно, линейно зависит от числа разрядов слагаемых:
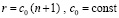, (14)
значение c0 определяется техническими параметрами связи соседних элементов.
Из изложенного вытекает
Теорема 1. Пусть требуется выполнить бинарное сложение двоичных полиномов степени n из (1), (2). Пусть сумматор с представленной выше структурой реализует алгоритм из четырех описанных выше шагов. Тогда, каково бы ни было произвольно заданное n, рассматриваемый сумматор, работая параллельно по всем разрядам, без использования логической схемы вычисления переноса, найдет искомую сумму за время t = O(1). При этом число элементов сумматора составит O(n). Сложность схемы в целом оценивается в виде:
t(r) = O(1), r = O(n). (15)
Шаги 3 и 4 можно совместить, что взамен (13) повлечет t(r) =3cτ, где r из (14).
О распространении алгоритмической структуры метода на другие позиционные системы счисления. Алгоритмическая основа предложенного метода непосредственно переносится на целочисленные полиномы с любым натуральным основанием степени, большим единицы, соответственно с натуральными коэффициентами, меньшими основания. Иными словами, метод применим в любой позиционной системе счисления с натуральным основанием. После выполнения первого шага вертикальной обработки цепочки переноса отделятся друг от друга коэффициентами, заведомо меньшими, чем элементы этой цепочки. Цепочку переноса составит наибольший коэффициент системы счисления (он на единицу меньше основания системы счисления), цепочка переноса горизонтально разместится в верхней разрядной сетке. В нижнюю разрядную сетку попадут значения основания системы счисления со сдвигом по диагонали согласно весу разряда вертикального сложения. Точнее, в нижнюю разрядную сетку попадут единичные коэффициенты с весом сдвинутого на разряд влево основания системы счисления. Слева по диагонали под всей цепочкой переноса в нижней разрядной сетке расположатся нули. Справа, в младшем разряде цепочки переноса, под наибольшим коэффициентом системы счисления верхней разрядной сетки, по вертикали, в нижней разрядной сетке расположится единица. Этот шаг можно проиллюстрировать на примере десятичной системы счисления. По аналогии с (8) выполнение первого шага вертикальной обработки влечет:
(16)
В (16) в нижней паре строк (в верхней и нижней разрядных сетках) получились две цепочки переноса:
и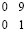 
.
По диагонали от девятки старшего разряда цепочки всегда ноль. Любое другое значение коэффициента означало бы суммирование по вертикали в рассматриваемом старшем разряде двух чисел, не больших 9, сумма которых оказалась бы не меньше 19. По этой же причине 0 располагается под каждой цифрой 9 данной цепочки переноса, за исключением ее младшего разряда, в котором всегда вертикальная пара 
, начинающая цепочку переноса. В верхней разрядной сетке цепочку переноса слева ограничивает некоторое число, всегда меньшее 9. В обеих разрядных сетках цепочку переноса слева от старшего разряда ограничивает вертикальная пара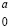 
, где a < 9. Справа от младшего разряда цепочку переноса ограничивает вертикальная пара 
, где b < 9, или, 
, где c < 9. В случае если эта вертикальная пара есть 
, то в верхней разрядной сетке справа, в соседнем младшем разряде должно быть число, меньшее 9. Цепочка чисел, не содержащая переноса, в младшем (и ни в каком другом) разряде не включает граничную пару 
. Если есть 1 в нижней разрядной сетке, то по вертикали в верхней разрядной сетке будет число меньшее 9: 
, где c < 9.
Таким образом, после первого шага вертикального сложения цепочки переноса взаимно разделены, и ни в один разряд не может прийти одновременно два ненулевых коэффициента. Такие цепочки переноса можно обрабатывать взаимно независимо и независимо от цепочек чисел, не содержащих переноса. Ввиду специфики вида цепочек переноса
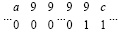, где a < 9, c < 9,
или
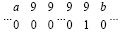, где a < 9, b < 9,
эти цепочки можно обрабатывать аналогично случаю двоичной системы. Именно: 9 можно заменить на –1, а по диагонали вместо нуля дописать +1. Это равносильно тождеству 9 = –1 + 10. В результате получится:
,
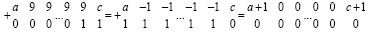где a < 9, или, соответственно,
,
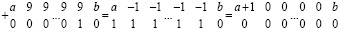где a < 9, и, следовательно, перенос выполнен в обоих случаях. При этом обработка сохраняет параллельность по всем разрядам. Без применения электронно-логического выделения цепочек, не содержащих переноса, остается сделать еще один, заключительный, шаг вертикального сложения, чтобы в верхней разрядной сетке получился окончательный десятичный результат сложения двух многоразрядных десятичных чисел.
Так, в примере (16) получится:
(17)
То же можно получить, заменяя в цепочках переноса 9, а также 1 младшего разряда в нижней разрядной сетке на 0, а в верхней разрядной сетке добавив 1 к значению разряда, соседнего со старшим разрядом цепочки переноса:
(18)
Очевидно, (18) эквивалентно (17).
В общем случае позиционной системы счисления с натуральным основанием v достаточно повторить изложенные рассуждения, заменив наибольший коэффициент 9 десятичной системы на наибольший коэффициент v – 1 системы счисления по основанию v. Пусть рассматривается такая система счисления и пусть требуется сложить два n + 1-разрядных целочисленных полинома с основанием степени v и с натуральными коэффициентами:
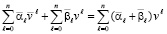, (19)
где
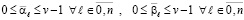. (20)
Как и в двоичной системе, сложение коэффициентов равного веса можно выполнять по вертикали, параллельно по всем разрядам:
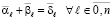, (21)
где все коэффициенты – натуральные числа, не большие v – 1, –
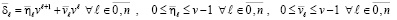. (22)
Параллельное по всем разрядам суммирование вида (21), (22), как и в случае двоичной системы, именуется первым шагом вертикального сложения. Как и прежде, при выполнении первого шага вертикального сложения перенос не распространяется, а результаты параллельного по всем разрядам суммирования коэффициентов равного веса в виде двухразрядных чисел (22) записываются параллельно по всем разрядам согласно весу коэффициентов – по диагонали, образуя двухрядный код в двух разрядных сетках:
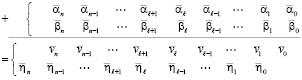(23)
верхняя разрядная сетка
нижняя разрядная сетка
При этом в нижней разрядной сетке могут располагаться исключительно нули или единицы: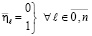 
.
Имеет место
Лемма 3. Пусть в позиционной системе счисления по основанию v требуется найти сумму двух полиномов (19), (20), и пусть выполнен первый шаг вертикального сложения вида (21) – (23). Тогда любая цепочка переноса примет вид:
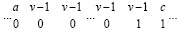, 0 ≤ a < v – 1, 0 ≤ c < v – 1, (24)
или
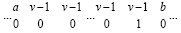, 0 ≤ a < v – 1, 0 ≤ b < v – 1. (25)
При этом две ближайшие друг к другу цепочки переносов необходимо отделятся друг от друга хотя бы одной вертикальной парой значений равного веса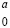 
, где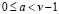 
. По крайней мере, одна из таких вертикальных пар необходимо располагается слева от значения v – 1, в разряде на единицу большего веса, чем старший разряд цепочки переноса.
Доказательство. Неравенство 0 ≤ a < v – 1 выполнено в силу того, что a обрывает цепочку переноса. Любое значение вместо нуля в паре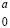 
означало бы априорное суммирование по вертикали в старшем разряде цепочки переноса двух коэффициентов, сумма которых не меньше v + v – 1 = 2v – 1, что невозможно, поскольку по вертикали складываются два коэффициента равного веса, каждый из которых не больше v – 1, и, таким образом, сумма не больше 2v – 2. Значения справа от цепочки переноса обусловлены тем, что вертикальная пара 
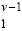начинает цепочку переноса. При этом диагональная запись 
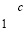или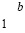 
не может совпадать c 
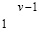. Лемма доказана.
Лемма 4. В условиях леммы 3 любая цепочка переноса может быть эквивалентно преобразована к виду:
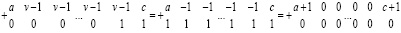, (26)
или
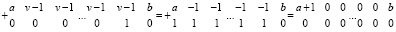, (27)
образуя в верхней разрядной сетке окончательный однорядный код результата переноса.
Доказательство. Запись результата первого вертикального шага сложения по диагонали вида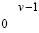 
означает, что сумма по вертикали в разряде веса 
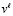равна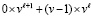 
.
Эта сумма тождественно преобразуется в цепочке равенств
.
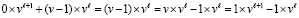Последнее равенство в двух разрядных сетках (23) в диагональной записи примет вид: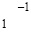 
. Последующее поразрядно-параллельное сложение по вертикали влечет правую часть равенств (26), (27). Лемма доказана.
Следствие 4. В условиях леммы 3 любая цепочка переноса может быть эквивалентно преобразована к виду:
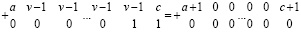, (28)
или
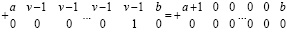, (29)
образуя в верхней разрядной сетке окончательный однорядный код результата переноса.
Доказательство непосредственно следует из (26), (27).
Равенства (28), (29) означают, что в любой позиционной системе счисления по натуральному основанию v после первого вертикального шага сложения любая цепочка переноса преобразуется в однорядный код с окончательно реализованным распространением переноса следующим образом. Каждое значение v – 1 верхнего ряда цепочки нужно заменить на ноль, заменить на ноль нужно также единицу нижнего ряда в младшем разряде цепочки, и, кроме того, следует прибавить единицу к значению разряда, соседнего со старшим разрядом цепочки переноса.
Очевидно, после первого шага вертикального сложения любая цепочка переноса необходимо отделена с обеих сторон от каждой соседней цепочки коэффициентов, не содержащей переноса, слева и справа ограничителями из (24), (25). Поэтому любая цепочка промежуточных между цепочками переноса значений, не содержащая переноса, может быть отделена вместе с входящими в нее единицами нижней разрядной сетки. В частности, это можно сделать с помощью схемы, в целом аналогичной схеме на рисунке, и разместить значения отделенных разрядов, например, в резервной паре верхней и нижней разрядных сеток. Затем отделенные значения разрядов можно параллельно по всем разрядам сложить с единицами по вертикали. Диагональная запись суммы не понадобится, поскольку по вертикали складываются числа, сумма которых меньше основания системы счисления v. Такое преобразование можно выполнить одновременно для всех цепочек коэффициентов, не содержащих переноса. Тогда в верхней разрядной сетке исходной пары разрядных сеток останутся цепочки переноса, которые одновременно преобразуются параллельно по всем разрядам согласно лемме 4 и следствию 4. Таким образом, в любой позиционной системе счисления с натуральным основанием v можно выполнять поразрядно-параллельное сложение чисел. При этом с техническими оговорками могут сохраниться оценки времени сложения и числа компонентов сумматора вида (15).
Все изложенные свойства верны для двоичной позиционной системы счисления, если положить v = 2, что было использовано выше в структуре параллельного сумматора. Свойства сохраняются для десятичной системы счисления, как описано выше, если положить v = 10.
Обсуждение. Предложенная структура параллельного сумматора отличается от аналогов тем, что не является результатом синтеза схем переноса на основе булевых формул и функций. Она не использует также схему Когге–Стоуна, часто применяемую для каскадирования ускоренного переноса по всем разрядам слагаемых. Предложенный сумматор реализует элементарные операции сложения битовых коэффициентов двоичных полиномов равного веса параллельно по всем разрядам слагаемых. После предварительного шага сложения по вертикали переносы взаимно отделяются промежуточными парами нулевых коэффициентов равного веса, что сводит дальнейший процесс к физическому разделению цепочек переноса от цепочек единиц без переноса. Разделение реализуется за время однократного переключения элементов. После этого, с точностью до непринципиальных оговорок, повторяется параллельное по всем разрядам сложение коэффициентов равного веса. Результатом является окончательное значение однорядной двоичной суммы двух двоичных полиномов степени n с оценкой времени сложения O(1) на O(n) разрядных элементах. Известные методы синтеза параллельных сумматоров имеют логарифмическую нижнюю оценку глубины схемы переноса, время сложения в них оценивается как O(log2n). Прототип предложенного сумматора ранее был описан в [17, с. 158; 18, с. 57], но при этом не использовалось электронно-логическое отделение цепочек без переноса, без чего количество элементов сумматора составляло не менее O(n2) элементов. Предложенная структура сумматора соответствует методу поразрядно-параллельной групповой обработки потока арифметических операций, рассмотренному в [17, с. 147; 18, с. 149], и может упрощать получение окончательной суммы и произведения. Упрощение очевидным образом распространяется на случай применения дополнительного кода для вычитания, рассматривавшегося в [18, с. 153], позволяя выполнить бинарное вычитание n+1-разрядных двоичных полиномов за время O(1) на сумматоре из O(n) элементов. Нетрудно видеть, что сумматор с предложенной структурой позволяет существенно увеличить разрядность данных, в результате повысить точность вычислительной обработки, что актуально в процессах численного моделирования. Отличительное качество изложенного подхода состоит в том, что он переносится на сложение чисел в произвольной позиционной системе счисления с натуральным основанием. В заключение можно указать на применимость параллельного сумматора с предложенной структурой для поразрядно-паралельного сравнения слов в методах поиска.
Заключение
В работе показана возможность выполнения бинарного многоразрядного арифметического сложения без вычисления переноса. Сложение двоичных полиномов степени n выполняется параллельно по всем n + 1 разрядам за единичное время с линейным количеством элементов сумматора: t(n) = O(1). Предложенная структура параллельного сумматора использует арифметические свойства сложения и позиционной двоичной системы счисления без преобразований булевых формул и функций, при этом исключается логарифмическая глубина схемы переноса. В целом метод сложения распространяется на произвольные позиционные системы счисления по натуральному основанию. Актуальные приложения связаны с ускорением потоковой обработки групповых арифметических операций и с увеличением точности вычислений в процессах численного моделирования.
Библиографическая ссылка
Ромм Я.Е. О ПОРАЗРЯДНО-ПАРАЛЛЕЛЬНОМ СЛОЖЕНИИ ДВОИЧНЫХ ПОЛИНОМОВ ЗА ЕДИНИЧНОЕ ВРЕМЯ ПРИ КОЛИЧЕСТВЕ ЭЛЕМЕНТОВ СУММАТОРА, ПРОПОРЦИОНАЛЬНОМ ЧИСЛУ РАЗРЯДОВ // Современные наукоемкие технологии. – 2025. – № 1. – С. 29-45;URL: https://top-technologies.ru/ru/article/view?id=40276 (дата обращения: 23.02.2025).