Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ромм Я.Е. 1 Тюшнякова И.А. 1

---

1 Таганрогский институт имени А.П. Чехова (филиал) ФГБОУ ВО «Ростовский государственный экономический университет (РИНХ)»

Целью работы является представление метода компьютерной идентификации средних значений по формулам Лагранжа и Коши. Средние значения определяются как минимумы модуля функции, состоящей из разности отношения приращения функции к приращению аргумента и производной на отрезке приращения. Минимум модуля функции идентифицируется по программе, без изменения заимствованной из метода идентификации нулей полиномов на основе устойчивой адресной сортировки. Предложены видоизменения теорем Лагранжа и Коши, при которых от входных функций не требуется непрерывность, а их средние значения выражаются через средние значения других, произвольно взятых функций, удовлетворяющих условиям теорем Лагранжа и Коши. Представлены различные примеры программной идентификации средних значений по классическим и видоизмененным формулам. Показано, что предложенный метод является частным случаем общего метода решения функциональных уравнений от одной действительной переменной, особенности его применения иллюстрируются на наглядных примерах. Отличительным качеством метода является ненакопление погрешности. Это достигается вследствие того, что метод не преобразует входные данные, а только сравнивает их, как того требует сортировка. При спуске к локализованному значению также используются только операции сравнения. Погрешность возникает единственно на входе метода при вычислении значений входных функций для последующих сравнений. Приводится код использованной программы, описаны результаты численных экспериментов. Отмечены возможные применения метода, одно из которых относится к компьютерному анализу устойчивости в смысле Ляпунова.

Статья в формате PDF

1430 KB

средние значения

формулы Лагранжа и Коши

видоизменение теорем о средних значениях

устойчивая сортировка слиянием

компьютерная идентификация средних значений

решение функциональных уравнений

1. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 1. СПб.: Лань, 2018. 608 с.

2. Ромм Я.Е. Об условиях устойчивости с обратной пропорцией начальным значениям решений систем обыкновенных дифференциальных уравнений // Современные наукоемкие технологии. 2023. № 9. С. 31–60. DOI: 10.17513/snt.39760.

3. Ромм Я.Е. Идентификация нулей и экстремумов функций на основе сортировки с приложением к анализу устойчивости. I. Случай одной действительной переменной // Современные наукоемкие технологии. 2020. № 6-1. С. 79–97. DOI: 10.17513/snt.38075.

4. Ромм Я.Е. Идентификация нулей и экстремумов функций на основе сортировки с приложением к анализу устойчивости. II. Случай двух действительных и одной комплексной переменной // Современные наукоемкие технологии. 2020. № 6-2. С. 254–282. DOI: 10.17513/snt.38101.

5. Ромм Я.Е. О границах идентификации корней полиномов на основе устойчивой адресной сортировки // Современные наукоемкие технологии. 2021. № 12-1. С. 84–108. DOI: 10.17513/snt.38959.

6. Заика И.В. Разработка и исследование схем оптимизации на основе алгоритмов сортировки с приложением к идентификации экстремумов решений дифференциальных уравнений: автореф. дис. … канд. техн. наук. Таганрог: ТРТУ, 2007. 19 с.

7. Джанунц Г.А. Методы обработки данных в информационно-вычислительных системах для моделей периодических процессов: автореф. дис. … докт. техн. наук. Таганрог: ЮФУ, 2023. 41 с.

8. Джанунц Г.А., Ромм Я.Е. Варьируемое кусочно-интерполяционное решение задачи Коши для обыкновенных дифференциальных уравнений с итерационным уточнением // Журнал вычислительной математики и математической физики. 2017. Т. 57, № 10. С. 1641–1660.

9. Демидович Б.П. Лекции по математической теории устойчивости. М.: Науку – всем, 2019. 480 с.

10. Гантмахер Ф.Р. Теория матриц. М.: Физматлит, 2010. 558 с.

11. Любимов В.В. Математическая теория устойчивости с приложениями. СПб.: Лань, 2018. 180 с.

12. Масина О.Н., Дружинина О.В., Рапопорт Л.Б. Элементы теории устойчивости математических моделей управляемых систем. Елец: Елецкий государственный университет им. И.А. Бунина, 2019. 143 с.

13. Поляк Б.Т., Хлебников М.В., Рапопорт Л.Б. Математическая теория автоматического управления. М.: ЛЕНАНД, 2019. 500 с.

14. Маркушевич А.И. Краткий курс теории аналитических функций. М.: Мир, 2006. 336 с.

15. Привалов И.И. Введение в теорию функций комплексного переменного. M.: Лань-Пресс, 2020. 442 с.

16. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 2. СПб.: Лань, 2019. 800 с

Введение

Теоремы о средних значениях принадлежат к основам математического анализа, являются наиболее популярными в теоретических исследованиях в области анализа. Формула Лагранжа имеет физическую трактовку: существует такой момент времени, в который мгновенная скорость движения равна средней скорости [1, с. 254]. Вместе с тем формулы Лагранжа и Коши относятся к типичным теоремам существования: они утверждают существование средних значений, но не указывают алгоритмов их вычисления. Знание средних значений востребовано во многих приложениях, однако общий способ их нахождения в научной литературе не представлен. Необходимость конструктивного алгоритма вычисления средних значений инициировалась исследованием устойчивости в смысле Ляпунова решений обыкновенных дифференциальных уравнений. Один из предложенных в [2, с. 51] критериев выражался через приращения решений и средние значения правых частей системы. Там же указывалось, как средние значения могут быть вычислены на основе устойчивой адресной сортировки, примененной к поиску корней функций одной действительной переменной. В излагаемой ниже работе рассматривается конструктивное решение этой задачи. Сравнительно подробно излагается принцип и особенности его программной реализации, заключающиеся в переносе на данную предметную область метода компьютерной идентификации корней полиномов. Выполняется исследование формальных разновидностей формул Лагранжа и Коши, а также программной реализации этих формул и их разновидностей.

Цель исследования – аналитически и с помощью численного эксперимента представить метод идентификации средних значений по формулам Лагранжа и Коши и показать связь предлагаемого метода с общим методом численного решения функциональных уравнений на основе устойчивой адресной сортировки.

Применение метода идентификации нулей функций на основе устойчивой адресной сортировки для идентификации средних значений. В [3, с. 81–87] изложен сравнительно общий метод идентификации нулей (корней – синоним будет применяться семантически равноценно без дополнительных оговорок) функций одной действительной переменной, в частности полиномов на основе устойчивой сортировки последовательности с взаимно однозначным соответствием входных и выходных индексов. Суть метода состоит в следующем. В любой числовой последовательности устойчивая адресная сортировка позволяет выделить все локально (и глобально) экстремальные элементы с помощью элементарных операторов. После сортировки последовательности с каждый ее локально минимальный элемент с входным индексом ek, 1 ≤ k ≤ N, в произвольном радиусе локализации r = ε0 идентифицируется по условию

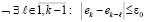. (1)

Фрагмент программной реализации условия (1) имеет вид

{выполнение процедуры сортировки sort}

k:=1; while k <= n do begin for L:=1 to k-1 do if abs(e[k]-e[k-L]) <= eps0 then goto 11; ilokmin:= e[k];

11: k:= k+1 end;

Здесь ilokmin – индекс локально минимального элемента в окрестности радиуса eps0 = ε0: оператор ilokmin:= e[k]; выполняется, если входной индекс e[k-L] любого элемента меньшего c[e[k]] (сk ) располагается от e[k] дальше, чем на eps0, в этом случае e[k] – индекс локально минимального элемента c[e[k]] в окрестности радиуса eps0. Если входной индекс e[k-L] хотя бы одного элемента c[e[k-L]] меньшего c[e[k]] расположен ближе чем на eps0 от e[k], элемент c[e[k]] не является минимальным в окрестности радиуса eps0 и пропускается путем перехода (goto 11;) к следующему номеру k. На вход сортировки с шагом дискретизации h поступают значения модуля функции, образующие входную последовательность. Пусть вначале рассматривается аналитическая функция в области поиска нулей. Тогда по принципу минимума модуля в результате выполнения (1) в окрестности радиуса ε0 окажется один и только один корень в некотором приближении. К нему выполняется спуск посредством итеративного сужения диаметра окрестности локализованного приближения до сближения концов диаметра меньше заданной границы абсолютной погрешности. Если функция не является аналитической, то минимум ее модуля идентифицируется непосредственно по построению в силу (1). В этом случае необходимо и достаточно непосредственно проверить значение минимума модуля на совпадение с нулем после окончания вычислений. Данный способ требует, чтобы радиус ε0 был выбран и зафиксирован меньше половины расстояния между ближайшими друг к другу соседними минимумами [3, с. 84]. Идентификация средних значений на этой же основе описывается непосредственно ниже. Именно, теорема Лагранжа о среднем значении согласно [1, с. 253] формулируется следующим образом.

Теорема 1. Пусть 1) функция f(x) определена и непрерывна в замкнутом промежутке [a, b], 2) существует конечная производная f'(x), по крайней мере, в открытом промежутке (a, b). Тогда между a и b найдется такая точка c (a < c < b), что для нее выполняется равенство

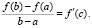(2)

Нули функции в предлагаемом методе идентифицируются как минимумы модуля функции. Поэтому от (1) выполняется переход к функции

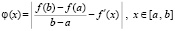, (3)

для (3) выполняется поиск минимумов на [a, b]. Программа (Delphi), реализующая метод, без изменения заимствуется из [3, с. 91], с той разницей, что она идентифицирует нули произвольной функции одной действительной переменной, а не корни полиномов, в таком виде она приводится непосредственно ниже:

program KORDEMINfuncLagrangeCauchy;

{$APPTYPE CONSOLE}

uses

SysUtils;

label 21, 22;

const

eps=1E-44; eps0=0.000049; h=eps0/40; n00=1512; mm=4;

x00=-1.2*1.3; x11=2*1.7;

type vect1=array [0..4*n00] of extended; vect2=array [0..4*n00] of longint;

var i,j,k,l,ee,nn0: longint;

aaa,x,x0,x1,xk,xk0,xk1,h0,min,eps1,hh,z,z1: extended;var c:vect1;var e:vect2;

function func (var x: extended): extended;

var p,p1,p11,p0,p00,p000:extended;

begin

func:=abs((sin(sqr(x11)-1)-sin(sqr(x00)-1))/(x11-x00)-2*x*cos(sqr(x)-1));

end;

procedure min1 (var x: extended;var ee:longint);

begin min:=func(x); ee:=0; for i:=1 to mm do begin

x:=xk0+i*h0; if min > func(x) then begin min:=func(x); ee:=i; end;end;end;

procedure sort(var nn0:longint; var c: vect1; var e: vect2);

type vecc=array[0..4*n00] of longint;

var ab:integer; i,j,k,l,m,r,nm,p,n: longint; e1, e2: vecc;

begin

p := trunc(ln(nn0)/ln(2)); if p<> ln(nn0)/ln(2) then p := p+1;

n := round(exp(p*ln(2)));

for l := 1 to n do if l<=nn0 then e[l] := l else ab:=1;

for r := 1 to p do begin m :=round(exp(r*ln(2))); nm:=n div m;

for k := 0 to nm-1 do begin

for l := 1 to m div 2 do begin

if (k * m + l > nn0) or (e[k * m + l]>nn0) then ab := l

else e1[l] := e[k * m + l];

if (k * m + m div 2+ l > nn0) or (e[k * m + m div 2+ l]>nn0) then ab := 1

else e2[l] := e[k * m + m div 2 + l] end;

i := 1; j := 0; while i + j <= m do begin

if i = m div 2 + 1 then ab := -1;

if j = m div 2 then ab := 1;

if (k * m + i > nn0) or (e[k * m + i]>nn0)

or (k * m + m div 2 + j > nn0-1) or (e[k * m + m div 2+ j]>nn0)

then ab:=1;

if (i <= m div 2) and (j <= m div 2 -1) and (k * m + i<= nn0)

and (k * m + m div 2 + j <= nn0-1)

then if (e2[j + 1] > nn0) or (e1[i]> nn0) then ab := 1 else

begin if c[e2[j + 1]] - c[e1[i]]= 0 then ab := 0;

if c[e2[j + 1]] - c[e1[i]]> 0 then ab := 1;

if c[e2[j + 1]] - c[e1[i]]< 0 then ab := -1

end; if ab >= 0 then

begin e[k * m + i + j] := e1[i]; i := i + 1 end

else begin e[k * m + i + j] := e2[j + 1]; j := j + 1 end

end end end end;

begin

aaa:=1e62; nn0:=n00; hh:=nn0*h;

x0:=x00; while x0 <= x11 do

while x0 <= x11 do

begin for i:=1 to nn0 do begin x:=x0+i*h; c[i]:=func(x); end;

sort(nn0, c, e); k:=1; while k<= nn0 do

begin for l := 1 to k-1 do if abs(e[k]-e[k-l]) <= eps0/h then goto 22;

xk:= x0+e[k]*h; eps1:=eps0; xk0:=xk-eps1; xk1:=xk+eps1; h0:=abs(2*eps1)/mm;

while abs(eps1) > eps do begin x:=xk0; min1(x,ee); eps1:=eps1/1.2;

xk0:=xk0+ee*h0-eps1; xk1:=xk0+ee*h0+eps1; h0:=abs(2*eps1)/mm; end;

if func(xk)= 0 then begin x:=xk; goto 21; end;

x:=xk0+ee*h0+eps1;

for i:= 1 to 2 do begin z:=x+i*h; if func(x) >= func(z) then goto 22; end;

for i:= 1 to 2 do begin z1:=x-i*h; if func(x) >= func(z1) then goto 22; end;

if abs(aaa-x)<=1e-20 then goto 22;

21: writeln (‘ ‘, x,’ ‘,(sin(sqr(x11)-1)-sin(sqr(x00)-1))/(x11-x00),’ ‘,2*x*cos(sqr(x)-1)); aaa:=x;

22: k:=k+1 end; x0:=x0 + hh end;

readln;

end.

Пример 1. Программа KORDEMINfuncLagrangeCauchy вычисляет средние точки функции

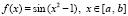, (4)

где a = –1.2*1.3, b = 2*1.7.

Для (4) составляется выражение производной 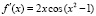и компонуется вспомогательная функция φ(x) вида (3), которая в подпрограмме function func (var x: extended): extended; реализуется в виде

func:=abs((sin(sqr(x11)-1)-sin(sqr(x00)-1))/(x11-x00)-2*x*cos(sqr(x)-1)).

Промежуток [a, b] в разделе описания констант задается операторами x00=-1.2*1.3; x11=2*1.7; Результат работы программы:

c 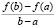f ʹ(c)

-3.09353239416177E-0001 -3.82506294187577E-0001 -3.82506294187577E-0001

1.63942706246943E+0000 -3.82506294187577E-0001 -3.82506294187577E-0001

2.37312244360731E+0000 -3.82506294187577E-0001 -3.82506294187577E-0001

2.98631356653877E+0000 -3.82506294187577E-0001 -3.82506294187577E-0001

В первом столбце выводится точка c среднего значения из (2). В третьем столбце выводится среднее значение производной f ʹ(c) из (2). Второй столбец взят для контроля правильности программы: в нем выводится 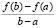из (2). Таким образом, приращение функции совпадает со средним значением.

Пример 2. Если промежуток [a, b] удлинить в 4 раза слева и справа от нуля (x00=-1.2*1.3*4; x11=2*1.7*4;), то для функции (4) получится

c 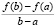f ʹ(c)

-6.09304693690835E+0000 3.77103058929846E-0002 3.77103058929845E-0002

-5.83009064921545E+0000 3.77103058929846E-0002 3.77103058929845E-0002

-5.55353356335865E+0000 3.77103058929846E-0002 3.77103058929846E-0002

-5.26375527885346E+0000 3.77103058929846E-0002 3.77103058929845E-0002

…………………………………………………………………………………………….

4.27588227867179E+0000 3.77103058929846E-0002 3.77103058929846E-0002

4.62777245438890E+0000 3.77103058929846E-0002 3.77103058929845E-0002

4.95638468302221E+0000 3.77103058929846E-0002 3.77103058929846E-0002

5.26307467286399E+0000 3.77103058929846E-0002 3.77103058929846E-0002

……………………………………………………………………………………………

1.32423493431969E+0001 3.77103058929846E-0002 3.77103058929843E-0002

1.33603358359356E+0001 3.77103058929846E-0002 3.77103058929847E-0002

1.34774988997091E+0001 3.77103058929846E-0002 3.77103058929845E-0002

1.35934463311493E+0001 3.77103058929846E-0002 3.77103058929842E-0002

Если промежуток [a, b] уменьшить в 4 раза слева и справа от нуля (x00=-1.2*1.3/4; x11=2*1.7/4;), то идентифицируется всего одна средняя точка:

c 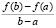f ʹ(c)

3.10209118743417E-0001 3.83823093645001E-0001 3.83823093645001E-0001

Пример 3. Пусть

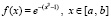, (5)

тогда 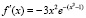, для (5) компонуется модуль разности вида (3):

func:=abs((exp(-x11*sqr(x11)+1)-exp(-x00*sqr(x00)+1))/(x11-x00)+3*sqr(x)*exp(-x*sqr(x)+1));

и на том же промежутке (x00=-1.2*1.3/4; x11=2*1.7/4;) результат работы программы примет вид

c 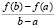f ʹ(c)

-3.64904360559138E-0001 -1.13992358309859E+0000 -1.13992358309859E+0000

3.84671652319215E-0001 -1.13992358309859E+0000 -1.13992358309859E+0000

На малых отрезках в окрестности заданной точки вычисления производной, например, на отрезке 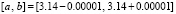для той же функции получится

c 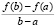f ʹ(c)

3.13999999952860E+0000 -2.88329869261089E-0012 -2.88329869261089E-0012

Пример 4. На отрезке 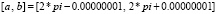для функции 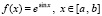, , 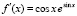получится среднее значение, близкое к значению производной в центре [a, b]:

c 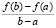f ʹ(c)

6.28318530717959E+0000 1.00000000000000E+0000 1.00000000000000E+0000

Численный эксперимент показывает достоверность работы программы на множестве корректно определенных в условиях теоремы 1 и в языке программирования функций.

Аналогично идентифицируются средние значения формулы Коши. Именно, согласно [1, с. 257] теорема Коши о среднем значении формулируется следующим образом.

Теорема 2. Пусть 1) функции f(x) и g(x) определены и непрерывны в замкнутом промежутке [a, b]; 2) существуют конечные производные f ʹ(x) и gʹ(x), по крайней мере, в открытом промежутке (a, b); 3) 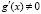в промежутке (a, b). Тогда между a и b найдется такая точка c0 (a < c0 < b), что

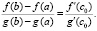(6)

От (6) выполняется переход к функции

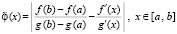, (7)

для которой выполняется поиск минимумов на [a, b].

Пример 5. Программа KORDEMINfuncLagrangeCauchy согласно (7) вычислит средние точки функций

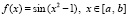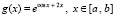, , (8)

при .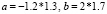

Для (8) составляются аналитические выражения производных 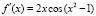, 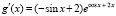. Из функций и производных компонуется вспомогательная функция 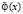вида (7). Ее реализация в подпрограмме function func (var x: extended): extended; примет вид:

func:=abs((sin(sqr(x11)-1)-sin(sqr(x00)-1))/(exp(cos(x11)+2*x11)-exp(cos(x00)+2*x00))- 2*x*cos(sqr(x)-1)/((2-sin(x))*exp(cos(x)+2*x)));

Результат работы программы:

c0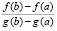

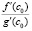
-2.68137968046213E-0002 -5.55711882250242E-0003 -5.55711882250242E-0003

1.61631844691806E+0000 -5.55711882250242E-0003 -5.55711882250242E-0003

2.37206383332615E+0000 -5.55711882250242E-0003 -5.55711882250242E-0003

3.02108361296119E+0000 -5.55711882250242E-0003 -5.55711882250242E-0003

3.37147901438510E+0000 -5.55711882250242E-0003 -5.55711882250242E-0003

Согласно эксперименту программа работает правильно на множестве функций, корректно определенных в условиях теоремы 2 и в языке программирования.

Применение метода для видоизмененных формул Лагранжа и Коши. Теорема Лагранжа допускает видоизменение, которое связывает между собой приращения и производные двух произвольно взятых и различных между собой функций в точках средних значений. Именно, имеет место

Предложение 1. Пусть для функции f(x) выполнены все условия теоремы 1 в замкнутом промежутке [a, b], а для ее производной f ʹ(x) – в открытом промежутке (a, b), и согласно этой теореме 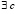, такое, что верно равенство

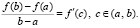(9)

Пусть для некоторой другой функции g(x) все те же условия выполнены на [a, b], для ее производной gʹ(x) – на (a, b), и, следовательно, 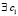, такое, что верно равенство

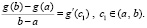(10)

Тогда, есл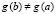и и 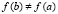, то наряду с (9) и (10) верно равенство

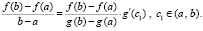(11)

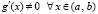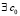Если в этих условиях , то , такое, что

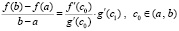, (12)

при этом

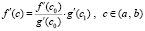, (13)

где три средние точки c, c0 , c1 из промежутка (a, b), вообще говоря, различны.

Доказательство. С учетом того, что для всех рассматриваемых в доказываемой теореме функций и их производных выполнены все соответственные условия теорем 1, 2, правомерны следующие элементарные преобразования. Умножение обеих частей (11) на дробь 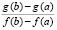влечет (10), умножение обеих частей (10) на 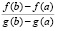влечет (11), так что эти равенства эквивалентны. Замена в (11) 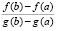на правую часть (6) влечет (12). Левая часть (12) совпадает с правой частью (9), что влечет (13). Предложение доказано.

Чтобы вычислить средние точки по формулам (12), (13), вначале надо вычислить дробный коэффициент 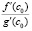. Это получится по теореме Коши согласно формуле (6), если перейти к (7) и подать такую функцию на вход программы KORDEMINfuncLagrangeCauchy.

После нахождения коэффициента нужно составить новую функцию вида

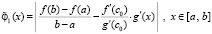(14)

и подать эту функцию на вход той же программы. Искомые средние точки c1 получатся как нулевые минимумы модуля (14) на (a, b), а значение gʹ(c1) получится непосредственной подстановкой c1 в выражение производной gʹ(x).

Пример 6. Пусть взяты функци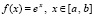и и 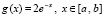. Их производные соответственно 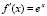и 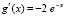. Пусть .

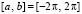Функция (7) примет вид

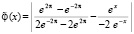, или, после преобразования, .

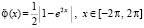В операторах программы func:=abs(1-exp(2*x))/2; Результат работы программы:

c0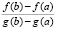

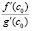
-1.35525271560688E-0020 -5.00000000000000E-0001 -5.00000000000000E-0001

Равенство (12) примет вид .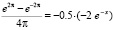

На вход программы поступит выражение 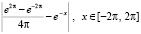, которое в операторах программы запишется как func:=abs((exp(2*pi)-exp(2*(-pi)))/(4*pi) -exp(-x));

Окончательный результат работы программы:

c1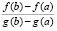

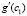
-3.75215757286186E+0000 -5.00000000000000E-0001 -8.52258467484871E+0001

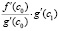
4.26129233742435E+0001

Соотношение (13) можно получить непосредственно из формул Лагранжа и Коши. Если в условиях теоремы 3 выполнено (9) и (10), то деление левых и правых частей повлечет

.

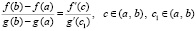Согласно теореме Коши

.

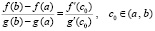Отсюда правые части равны,

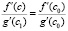, (14)

что влечет (13). Ниже последовательность данных соотношений реализуется по программе KORDEMINfuncLagrangeCauchy.

Пример 7. Если , , ,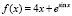

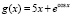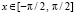то , , .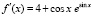

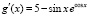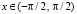Функции вида (3) примут вид ,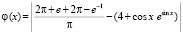

или, 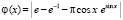, и, соответственно,

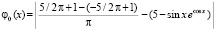, или, .

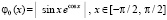В программной реализации

первая из функций func:=abs(exp(1)-exp(-1)-pi*cos(x)*exp(sin(x)));

вторая функция, соответственно, func:=abs(sin(x)*exp(cos(x)));

Результаты работы программы KORDEMINfuncLagrangeCauchy для этих функций раздельно приводятся непосредственно ниже

c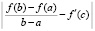

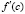
-2.59086855641386E-0001 0.00000000000000E+0000 4.74815631638363E+0000

1.27963743139017E+0000 0.00000000000000E+0000 4.74815631638363E+0000

и

c1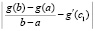

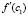
1.74749833825092E-0045 4.75019297812984E-0045 5.00000000000000E+0000

Левая часть (14) примет значения, располагаемые ниже в третьем столбце:

c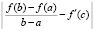

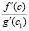
-2.59086855641386E-0001 0.00000000000000E+0000 9.49631263276725E-0001

1.27963743139017E+0000 0.00000000000000E+0000 9.49631263276725E-0001

То же получится по теореме Коши, именно,

,

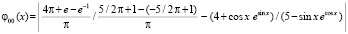или, .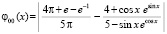

В программной реализации –

func:=abs((4*pi+exp(1)-exp(-1))/(5*pi)-(4+cos(x)*exp(sin(x)))/(5-sin(x)*exp(cos(x)))).

Результат работы программы:

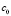
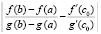
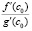
-7.05355879518969E-0002 5.42101086242752E-0020 9.49631263276725E-0001

Тем самым формула (14) на данном примере получила программное подтверждение.

Аналогично предложению 1 в дальнейшем приводится видоизменение теоремы Коши.

Дополнительные видоизменения теорем Лагранжа и Коши. Связь приращения одной функции с производной другой функции является более общей, чем показано выше. Это иллюстрируют приводимые ниже утверждения.

Лемма 1. Пусть для каждой из различных функций f(x) и g(x), а также для их производных выполнены все условия теоремы 1 на промежутке [a, b]. Тогда, если на этом промежутке равны приращения

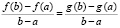, (15)

то 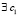, такое, что верно равенство

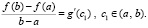(16)

Доказательство. По теореме 1 для функции g(x) выполнено (10). В силу условия (15) равенство (10) перейдет в равенство (16). Лемма доказана.

Имеет место

Предложение 2. Пусть для различных функций f(x) и g(x) выполнены все условия теоремы 1 на промежутке [a, b] и для определенности 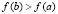. Если 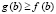и , то и 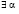, такие, что выполняется соотношение

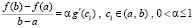. (17)

Данное утверждение и соотношение (17) сохраняются в случае 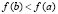, есл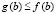и и 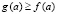. Кроме того, в рассматриваемых условиях 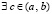, такое что

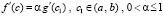. (18)

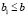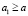Доказательство. Поскольку функция g(x) непрерывна, то найдутся точки и , такие, что 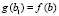и 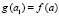. Если 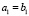, то искомое утверждение непосредственно следует из леммы 1. Пусть рассматривается случай 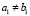. В этом случае на промежутке 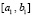для функции g(x) выполнены все условия теоремы 1, и согласно этой теореме 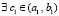, такое, что

.

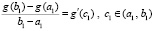Отсюда, с учетом , ,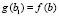

,

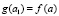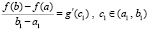и, таким образом,

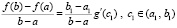. (19)

Поскольку 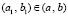, то 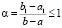, кроме того, 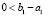, поэтому из (19) следует (17). Случай 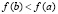при услови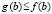и и 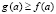рассматривается аналогично. Равенство (18) следует из теоремы Лагранжа применительно к левой части (17). Предложение доказано.

Следствие 1. Пусть для различных функций f(x) и g(x) выполнены все условия теоремы 1 на промежутке [a, b] и для определенности 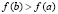. Если 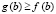, но 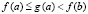, то утверждения теоремы 3 и соотношение (17) сохраняются со следующим видоизменением

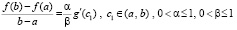. (20)

Это же утверждение и соотношение (20) сохраняются также в случае 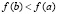, если 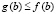и . Кроме того, в рассматриваемых условиях 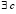, такое что

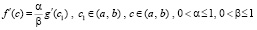. (21)

Доказательство. Пусть рассматривается случай 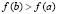при условии 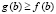, но 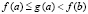. Пусть 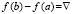. По непрерывности g(x) найдется промежуток 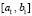, , 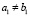, 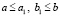такой, что .

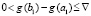Очевидно, .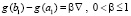

На промежутке 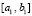для функции g(x) выполнены все условия теоремы 1. Согласно этой теореме 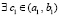, такое, что .

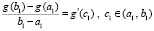Тогда 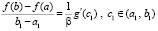. Отсюда

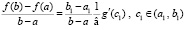. (22)

Поскольку 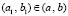, то , , 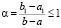кроме того, 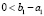. Поэтому из (22) следует (20).

Случай 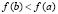при услови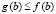и и 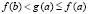рассматривается аналогично. Соотношение (21) – следствие теоремы Лагранжа применительно к левой части (20). Следствие доказано.

Предложение 2 и следствие 1, без требования непрерывности функции f(x), обобщает

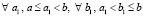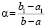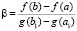Теорема 3. Пусть функция f(x) определена на промежутке [a, b]. Пусть, кроме того, функция g(x) определена и непрерывна на [a, b], и у нее существует конечная производная gʹ(x) на (a, b). Тогда ,, и , при условии 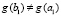, справедливо утверждение: 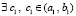, такое, что

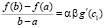. (23)

Если, кроме того, f(x) имеет конечную производную на (a, b), то 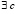, такое что

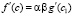. (24)

Доказательство. В условиях рассматриваемой теоремы верно тождество

.

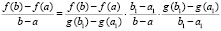На промежутке 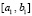для функции g(x) выполнены все условия теоремы 1.

Поэтому 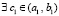такое, что 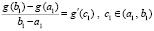. Отсюда следует (23).

Если, кроме того, функция f(x) непрерывна на [a, b] и существует конечная производная f’(x) на (a, b), то по теореме Лагранжа 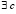такое, что 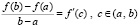, в этом случае (23) перейдет в (24). Теорема доказана.

Теорема 3 дает конструктивную возможность вычислить по программе KORDEMINfuncLagrangeCauchy среднюю точку и среднее значение для любой функции g(x) из условий теоремы. Сначала произвольно фиксируются точки a1, b1, в них вычисляются g(a1) и g(b1). Затем вычисляются значения дробе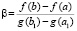й и .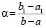

После этого составляется модуль разности 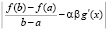, который в виде подпрограммы-функции func поступает на вход программы при значениях x00= a1; x11= b1. В результате работы программы идентифицируются искомые средние значения 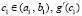. По той же программе 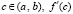можно найти, составив 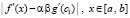, или, составив .

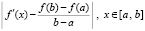Пример 8. Пусть

, ; , , .

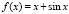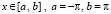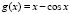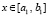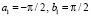В этом случае ;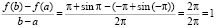

; ;

, .

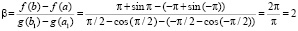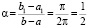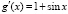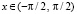Таким образом, .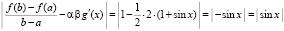

Для программы KORDEMINfuncLagrangeCauchy задаются границы x00=-pi/2; x11= pi/2; задается подпрограмма-функция func:=abs(sin(x)); в результате работы программы получится

c1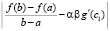

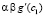
1.74749833825092E-0045 1.74749833825092E-0045 1.00000000000000E+0000

Иными словами, c1 = 0, 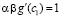и .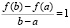

Если теперь положить , ,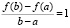

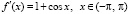, соответственно, выполнить x00=-pi; x11= pi;

func:=abs(cos(x)); то в результате работы той же программы получится:

c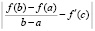

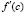
-1.57079632679490E+0000 2.71050543121376E-0020 1.00000000000000E+0000

1.57079632679490E+0000 2.71050543121376E-0020 1.00000000000000E+0000

В этом случае получились две средние точки с одинаковым значением в них производной, при этом значение производной совпало с предыдущим результатом, что подтверждает соотношение (24). В данном примере этот результат виден аналитически.

В общем случае теорема Лагранжа следует из теоремы 3 при 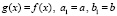, и при условии непрерывности функции f(x). Собственно в теореме 3 непрерывность f(x) для выполнения (23) не требуется.

Аналогично теореме 3 доказывается

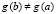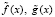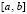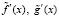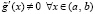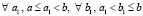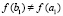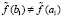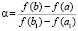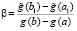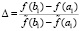Теорема 4. Пусть функции f(x), g(x) определены на промежутке [a, b] и . Пусть произвольно выбраны функции , которые определены, непрерывны на , у них существуют конечные производные на (a, b), и при этом . Тогда , таких, что , , при значениях , и , справедливо утверждение: 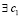, , 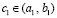такое, что

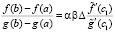. (25)

Если, кроме того, 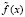имеет конечную производную на (a, b), причем 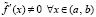, то 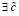,,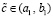 такое, что

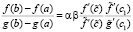. (26)

Если помимо этого g(x) имеет конечную производную на (a, b), причем 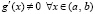, то 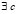, , 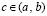такое, что

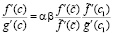. (27)

Доказательство опирается на тождественные преобразования

,

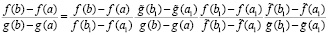и

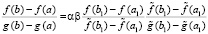, (28)

с переходом в правой (затем левой) части (28) к отношениям производных согласно теореме Коши, что влечет соответственно (25), (26) и (27).

Как нетрудно видеть, из теоремы 4 следуют теорема 3, а также теоремы 2 и 1.

О численном решении функциональных уравнений на основе устойчивой адресной сортировки. В представленных применениях метода на вход подавался модуль разности, например, из (3):

.

Метод имеет более общий характер – он применим для любых корректно заданных функций. В случае формулы Лагранжа функция φ(x) означала разновидность поиска минимума модуля функции

,

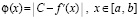где C = const – произвольно заданное число. В рассмотренных случаях .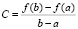

В случае формулы Коши рассматривалась константа 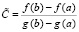и функция

.

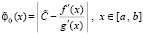В общем случае, если на вход метода подавать функцию

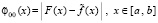, (29)

где обе функции под знаком модуля такие, что обосновано существование корня их разности, например, обе эти функции аналитические, то на основе программы KORDEMINfuncLagrangeCauchy будут идентифицированы все корни функции 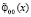, то есть все решения функционального уравнения

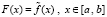. (30)

Пример 9. Пусть рассматривается уравнение 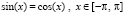. На вход метода подается 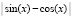, ищутся минимумы этой функции. Для программы KORDEMINfuncLagrangeCauchy задаются границы x00=-pi; x11=pi; определяется подпрограмма-функция func:=abs(sin(x)-cos(x)); в результате работы программы получится:

x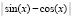

-2.35619449019234E+0000 1.62630325872826E-0019

7.85398163397448E-0001 5.42101086242752E-0020

Если вывести x/π, то результат примет вид

x/π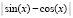

-7.50000000000000E-0001 1.62630325872826E-0019

2.50000000000000E-0001 5.42101086242752E-0020

В правой и левой частях (30) могут быть заданы производные любого порядка.

Пример 10.

Пусть 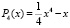и 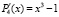. Требуется решить уравнение 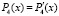, то есть найти действительные корни этого уравнения. Составляется модуль разности 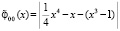, или, .

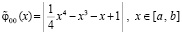Для программы KORDEMINfuncLagrangeCauchy задаются границы x00=-100; x11=100; определяется функция func:=abs(1/4*sqr(sqr(x))-x*sqr(x)-x+1); в результате работы программы получится

x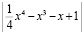

2.25351769306885E-0001 0.00000000000000E+0000

1.32879973565507E+0000 8.67361737988404E-0019

Остальные корни комплексные. Границы расположения корней определяются автоматически [4, с. 259; 5, с. 90] и достаточно быстро, если взять увеличенное, например, в 100 раз eps0=0.000049*100.

Пример 11. Если взять полином 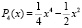и его производную 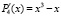, то рассматриваемый способ позволяет указать кратность корня с помощью дополнительного раздельного вывода значения полинома и его производной –

;

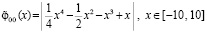x00=-10; x11=10; func:=abs(1/4*sqr(sqr(x))-1/2*sqr(x)-x*sqr(x)+x);

в результате работы программы получится

x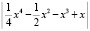

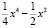
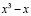
-3.51024200364276E-0001 0.00000000000000E+0000 -2.38323813456247E-0001 -2.38323813456247E-0001

3.58726976475287E-0045 1.12697403393924E-0044 -6.35035236586642E-0089 -1.12697403393924E-0044

2.71720304028491E-0001 5.42101086242752E-0020 -2.31597975776807E-0001 -2.31597975776807E-0001

1.35254344107095E+0000 8.67361737988404E-0019 7.24699217892331E+0001 7.24699217892331E+0001

Из второй строки (курсив) видно, что корень x = 0 является корнем одновременно полинома и его производной, тем самым это кратный корень полинома.

Если входную функцию на вход программы определять без модуля, то программа выдаст все минимумы этой функции, например

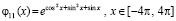. (31)

Программное представление функции (31) func:=exp(sqr(cos(x))+sqr(sin(x))+sin(x)); начало и конец промежутка x00=-4*pi; x11=4*pi; подаются на вход программы KORDEMINfuncLagrangeCauchy.

Результат работы программы:

x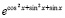

-7.85398163441007E+0000 1.00000000000000E+0000

-1.57079632723048E+0000 1.00000000000000E+0000

4.71238897994910E+0000 1.00000000000000E+0000

1.09955742871286E+0001 1.00000000000000E+0000

Если, для наглядности, выводить x/π, то результат примет вид

x/π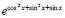

-2.50000000013865E+0000 1.00000000000000E+0000

-5.00000000138651E-0001 1.00000000000000E+0000

1.49999999986135E+0000 1.00000000000000E+0000

3.49999999986135E+0000 1.00000000000000E+0000

Если на вход метода подать функцию со знаком минус, а вывести результат с обратным знаком, то программа определит все максимумы функции. Для функции (30) на том же промежутке получится func:=-exp(sqr(cos(x))+sqr(sin(x))+sin(x)); результат работы программы:

x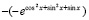

-1.09955742879675E+0001 7.38905609893065E+0000

-4.71238898078796E+0000 7.38905609893065E+0000

1.57079632639162E+0000 7.38905609893065E+0000

7.85398163357121E+0000 7.38905609893065E+0000

Если, для наглядности, выводить 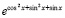/ 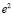, то результат примет вид

x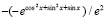

-1.09955742879675E+0001 1.00000000000000E+0000

-4.71238898078796E+0000 1.00000000000000E+0000

1.57079632639162E+0000 1.00000000000000E+0000

7.85398163357121E+0000 1.00000000000000E+0000

Все экстремумы определяются по местоположению и по значению.

Метод в целом переносится на функции двух [4, с. 255] и нескольких переменных [6, с. 6], при поиске корней функций метод переносится на случай функций комплексных переменных [4, с. 255]. При поиске действительных корней полиномов степени 12880 и выше корни идентифицируются с сохранением всех значащих цифр мантисс в формате представления данных при взаимной отделенности корней на 0.0001 [5, с. 92]. Все комплексные корни полинома с комплексными коэффициентами степени 220 идентифицируются с сохранением всех значащих цифр мантисс действительной и мнимой частей в формате представления данных в случае взаимной отделенности корней на 0.1 [5, с. 99].

О возможных применениях метода. Предложенная идентификация средних значений применима при вычислении интегралов и производных на основе кусочной интерполяции функции (в частности, на каждом подынтервале приближения) [7, с. 41]. Другое применение возможно для приближенного решения систем обыкновенных дифференциальных уравнений в случае использования варьируемого кусочно-интерполяционного решения задачи Коши (также на каждом подынтервале приближения решения и производной) [8, с. 1642]. Непосредственное применение метода целесообразно для компьютерного анализа устойчивости в смысле Ляпунова решений систем обыкновенных дифференциальных уравнений. Так, в [2, с. 51] приводится необходимое и достаточное условие устойчивости в терминах средних точек формулы Лагранжа. Во всех этих применениях предметом особого внимания должна быть погрешность интерполяции. Сам по себе предложенный метод выполняет только сортировку и спуск к локализованным значениям, при этом выполняются исключительно операции сравнения, чем обходится накопление погрешности. Погрешность возникает лишь при вычислении значений входной функции, в дальнейшем она не накапливается. Для линейных систем с постоянными коэффициентами базовый критерий устойчивости использует корни характеристического полинома и определение их кратности [9, с. 86; 10, с. 134], что достигается на основе охарактеризованного обобщения метода. В свою очередь, анализ устойчивости имеет широко известные технические и технологические применения [11, с. 3; 12, с. 7; 13, с. 83]. Относительно математического обоснования предложенного метода необходимо отметить следующее. Применение предложенного метода непосредственно для идентификации средних значений основано на существовании точек средних значений в условиях теорем Лагранжа и Коши. При видоизменении формул в условиях теоремы 3 существование точек средних значений для функций правой части (23) вытекает из теоремы Лагранжа. Для приращения левой части (23) эти точки переводятся в точки средних значений с помощью тривиально конструируемых коэффициентов 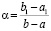и .

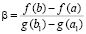Аналогичное утверждение можно сделать относительно существования точек средних значений в условиях теоремы 4. Собственно процесс программной идентификации искомых точек основан на построении алгоритма идентификации экстремальных элементов последовательности согласно (1). В более общем случае решения уравнений вида (30) метод опирается на принцип минимума модуля [14, с. 284; 15, с. 361], вследствие которого аналитическая функция под знаком модуля в (29) может достигать минимума модуля только в случае, если она обращается в нуль. Существует принципиальная возможность применения метода на основе теорем о средних значениях несобственных интегралов [16, с. 600].

Заключение

Изложен компьютерный метод идентификации средних значений по формулам Лагранжа и Коши. Метод основан на сортировке слиянием по матрицам сравнений. Сортировка устойчива, обладает взаимно однозначным соответствием входных и выходных индексов отсортированных элементов, ее применение позволяет избежать накопления погрешности. Предложены модификации формул Лагранжа и Коши, при которых от входной функции не требуется непрерывность на промежутке приращения. Метод является частным случаем общего метода решения функциональных уравнений, особенности его применения иллюстрируются на сравнительно большом количестве наглядных примеров.

Библиографическая ссылка