Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Шайдуллина Н.К. 1 Печеный Е.А. 1 Нуриев Н.К. 1

---

1 ФГБОУ ВО «Казанский национальный исследовательский технологический университет»

Целью исследования является получение зависимости между количеством каналов обслуживания и долей обработанных заявок в области систем массового обслуживания со смешанным входным потоком заявок, имеющих ограниченное время жизни. В публикации представлены результаты численной обработки смешанного потока заявок с ограниченным временем жизни. Получены зависимости между количеством каналов обслуживания и долей обработанных заявок. Для этого построена имитационная модель с программной реализацией, позволяющая варьировать не только входные параметры, но и управляющие механизмы. Рассмотрены простейшие потоки заявок и смешанные со случайным количеством требований, поступающих одномоментно. Исследованы системы с очередью и отказами, произведен сравнительный анализ результатов их деятельности. Установлено, что различные комбинации входных параметров влияют на количественный результат, но не влияют на тенденцию стремления к определенному состоянию. Представлены результаты численных расчетов для определенной комбинации входных параметров и заданных законов распределения случайных величин, которыми являются время между поступлением групп требований, время обслуживания заявки, количество заявок в группе. Проиллюстрированы графически зависимости доли обработанных заявок от количества каналов для систем с очередью и без, для систем, в которых вариативен один из показателей упомянутых законов распределения. Установлены предельные значения доли обработанных заявок, которые невозможно преодолеть введением дополнительных каналов обслуживания.

Статья в формате PDF

960 KB

система массового обслуживания

смешанный входной поток заявок

ограниченный срок жизни заявки

имитационная модель

1. Кирпичников А.П., Флакс Д.Б., Валеева Л.Р. Системы массового обслуживания с ограниченным средним временем пребывания заявки в системе и их вероятностные характеристики // ФӘн-наука. 2015. № 6(45). С. 5-9.

2. Шайдуллина Н.К., Печеный Е.А., Нуриев Н.К. Проблема эффективного администрирования системы массового обслуживания с ограниченным временем жизни заявок // Современные наукоемкие технологии. 2022. № 7. С. 69-73. DOI: 10.17513/snt.39235.

3. Постников В.М., Спиридонов С.Б., Терехов В.И. Методы и модели массового обслуживания в системах организационного управления: учебно-методическое пособие по дисциплине «Аналитические модели автоматизированных систем обработки информации и управления». М.: Спутник +, 2023. 261 с.

4. Рыжиков Ю.И. Расчет систем обслуживания с большим числом каналов // Информационные технологии и математическое моделирование (ИТММ-2018): материалы XVII Международной конференции имени А.Ф. Терпугова. Томск: Изд-во НТЛ, 2018. С. 132-138.

5. Бурлаков М.В., Подоляк Е.Е., Шаповал Е.И. О динамической сортировке заявок в системах с ограниченным временем пребывания // Автоматика и телемеханика. 1985. Выпуск 10. С. 39–43.

6. Кирпичников А.П., Томилова М.Н. Вероятностные характеристики открытых многоканальных систем массового обслуживания с частичной взаимопомощью между каналами // Вестник технологического университета. 2019. Т. 22, № 1. С. 92-96.

7. Старыгина С.Д., Нуриев Н.К., Печеный Е.А. Построение математической модели процесса регламентации педагогического тестирования // Информационные технологии и математическое моделирование (ИТММ-2017): материалы XVI Международной конференции имени А.Ф. Терпугова. Томск: Изд-во НТЛ, 2017. С. 223-229.

Введение

Работы в области систем массового обслуживания (СМО) с ограниченным временем пребывания заявок имеют безусловную актуальность, которая обусловлена обширностью их сферы применения. В качестве примера можно привести технологические производственные процессы, в которых время обслуживания заявки может быть ограничено ее физическими характеристиками или зоной действия обслуживающего устройства, через которую она проходит [1]. Другой немаловажной зоной применения могут служить торговые операции, в которых роль заявок с ограниченным временем жизни выполняют товары с ограниченным сроком годности [2]. В качестве еще одного примера СМО подобного типа можно указать процесс оказания неотложной помощи пациентам медицинских учреждениях, который требует проведения срочных манипуляций с ограниченным временем применимости. Безусловно, нельзя обойти вниманием и зону приложения, особенно актуальную в современных реалиях. Речь идет о системах организационного управления, в которых роль заявок выполняет информация, поступающая в случайные моменты времени и имеющая ограниченное время актуальности [3, с. 7]. Например, в информационных системах, являющихся частным случаем систем организационного управления, требования на обслуживание представляют собой запросы к серверам и могут иметь конечное время жизни ввиду быстрого старения информации.

Задачи поиска характеристик систем массового обслуживания с ограниченным временем жизни заявок рассматривались во многих работах и в разных постановках. Это одноканальные системы с детерминированным входным потоком заявок и определенным законом распределения времени обслуживания, одноканальные системы с простейшим входным потоком заявок, произвольным законом распределения времени обслуживания и временем ожидания, ограниченным постоянной величиной, многоканальные системы с пуассоновским входным потоком и экспоненциальным законом распределения времени обслуживания со случайным ограничением на время ожидания [4-6]. В некоторых из них были получены аналитические результаты для СМО определенного класса, но универсальных расчетных механизмов приемлемой сложности ни в одной работе предложено не было.

Универсальным расчетным средством в плане практической применимости может служить имитационное моделирование. Оно дает возможность задать закон распределения входного потока случайных величин, закон распределения времени обслуживания заявки, один на всех обслуживающих устройствах или индивидуально для каждого, обусловить процесс формирования очереди, задать характер потока требований (ординарный, групповой, смешанный).

Целью исследования является получение зависимости между количеством каналов обслуживания и долей обработанных заявок в СМО со смешанным входным потоком заявок, имеющих ограниченное время жизни. Для этого поставлены и решены следующие задачи: построение цифровой модели, программная реализация модели на языке C#, проведение имитационных экспериментов, анализ результатов.

Материалы и методы исследования

Входными параметрами имитационной модели являются: модельное время, срок жизни заявки – величина постоянная, одинаковая для всех требований, закон распределения времени между поступлением групп заявок – экспоненциальный, закон распределения времени обработки заявки – экспоненциальный, количество заявок в группе – случайная величина, распределенная равномерно. Имитационные эксперименты были выполнены как в условиях отсутствия очереди, так и при наличии опции ее накопления.

В случае наличия очереди предполагается, что потеря заявки может произойти как во время ожидания обслуживания при истечении срока жизни требования, так и на стадии обслуживания, если время обработки вкупе со временем ожидания оказалось больше времени жизни заявки. В системе без формирования очереди потеря может произойти при занятости всех обслуживающих устройств в момент поступления требования в систему и в ходе процесса обслуживания, если время, затраченное на обработку, больше времени жизни заявки.

В процессе работы над статьей выполнен ряд имитационных экспериментов, в которых варьировались значения параметров системы. Кроме того, для анализа результатов проведены опыты над ординарным потоком заявок с ограниченным временем жизни и по известным формулам (1, 2) вычислены значения относительной пропускной способности системы, обслуживающей простейший поток заявок с неограниченным временем жизни.

Для одноканальной СМО с отказами и неограниченным временем жизни заявок относительная пропускная способность системы вычисляется по формуле:

Q = (1 + ρ)–1 (1)

Для многоканальной СМО с отказами:

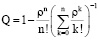, (2)

где ρ – средняя нагрузка на канал,

n – количество каналов.

Результаты исследования и их обсуждение

В таблице представлена часть численных результатов имитационных экспериментов для СМО с очередью и отказами, где:

T = 100000 врем. ед. – модельное время,

tend = 6 врем. ед. – срок жизни заявки,

t1 = 4 врем. ед. – среднее время между поступлением групп заявок – характеристика экспоненциального распределения,

t2 = 6 врем. ед. – среднее время обработки заявки – характеристика экспоненциального распределения,

количество заявок в группе равно 1 для ординарного потока или распределено равномерно от 1 до 4 (10).

Доля обработанных заявок для количества каналов от 1 до 20

В столбце «простейший» приведены расчеты для простейшего потока заявок с неограниченным временем жизни.

Для систем с наличием очереди при ρ > 1 одноканальная система попадает в поглощающее состояние и признается неработоспособной. При большем количестве обрабатывающих устройств условие возникновения поглощающего состояния преобразуется к виду:

.

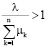где λ – интенсивность потока заявок,

μk – интенсивность k-го канала обслуживания,

n – количество каналов.

Данные таблицы показывают, что при небольшом количестве каналов обслуживания доля обработанных заявок для систем, работающих в условиях смешанного входного потока, значительно меньше, нежели при ординарном потоке. При увеличении числа обрабатывающих устройств до 8 единиц значимое различие сохраняется только для потока, где допустимое значение групповой составляющей велико, а при числе каналов более 20 различия практически исчезают.

Это наглядно демонстрирует графическая иллюстрация результатов работы алгоритма. Для системы без очереди она представлена на рисунке 1. Здесь «смешанный 4» и «смешанный 10» означают смешанный поток заявок, в котором одномоментно может появиться от 1 до 4 или от 1 до 10 заявок соответственно.

На рисунке 2 представлены результаты работы алгоритма для СМО с бесконечной очередью и теми же входными параметрами. Заметим, что «бесконечность» очереди означает лишь отсутствие в модели ограничений на ее длину. Физически же, в силу конечного времени жизни заявок, очередь будет ограниченной, независимо от значений интенсивностей входного потока заявок и потока обслуживания.

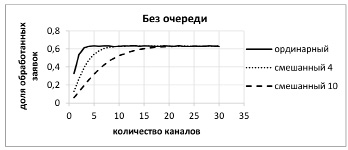
Рис. 1. Зависимости доли обработанных заявок от количества каналов в СМО без очереди

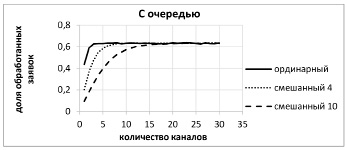
Рис. 2. Зависимости доли обработанных заявок от количества каналов в СМО с очередью

Рисунки 1 и 2 показывают, что по мере увеличения числа обслуживающих устройств доля обработанных заявок системами, обслуживающими смешанные потоки, довольно быстро приближается к соответствующим значениям, которые достигаются системой, функционирующей в условиях ординарного входного потока. Это обусловливает целесообразность его использования в качестве базы сравнения.

На следующем этапе средствами имитационного моделирования исследовалась зависимость доли полностью обработанных заявок от количества каналов обслуживания в системах, работающих в условиях смешанного входного потока требований, где предусмотрена опция накопления очереди.

В первой серии опытов варьировались значения срока жизни заявок в промежутке от 4 до 8 с шагом 2. При этом среднее время между поступлением групп заявок t1 было принято равным 4; среднее время обработки заявки t2 = 6; принята гипотеза о равномерном распределении числа заявок в группе от 1 до 4. Графическая иллюстрация результатов данного численного эксперимента представлена на рисунке 3.

Во второй серии варьировалось среднее время обработки заявки t2 от 4 до 8 также с шагом 2. При этом средняя длина интервала между поступлением групп заявок t1 = 4; продолжительность времени жизни заявок tend = 6; гипотеза о законе распределения и числе заявок в составе группы та же, что и в первой серии опытов. На рисунке 4 результаты этой серии представлены графически.

Графическое представление результатов первой и второй серии имитационных экспериментов позволяет с уверенностью утверждать, что с увеличением срока жизни заявок и сокращением среднего времени ее обработки количество требований, которое сможет обслужить система, возрастает. Стоит также обратить внимание на вид полученных зависимостей: все они имеют ярко выраженное «плато». Это свидетельствует о том, что при достижении определенного уровня, зависящего от интенсивности обслуживания и времени жизни заявок, дальнейшее наращивание ресурсов (каналов обслуживания) становится нецелесообразным. Данный результат согласуется с выводами авторов, представленными в работе [7].

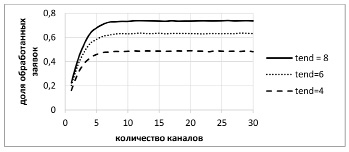
Рис. 3. Варьирование срока жизни заявок

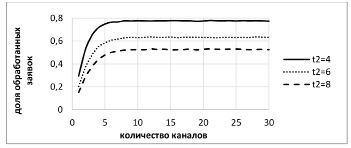
Рис. 4. Варьирование среднего времени обработки заявки

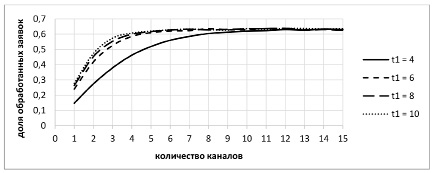
Рис. 5. Варьирование среднего времени между поступлением групп заявок

В третьей серии имитационных экспериментов изучалось влияние интенсивности входного потока заявок, для чего варьировалось среднее время между поступлением групп заявок t1 от 4 до 10 с шагом 2 при среднем времени обслуживания t2 = 6, времени жизни tend = 6 и равномерном распределении заявок внутри группы от 1 до 4 (рис. 5).

Результаты третьей серии опытов практически полностью аналогичны тем, что были получены в первых двух сериях. С увеличением числа действующих каналов доля заявок, обслуженных в полном объеме, быстро растет, стремясь к некоторому предельному значению, которое практически не обнаруживает зависимости от интенсивности входного потока.

Заключение

В работе изучено поведение СМО со смешанным входным потоком заявок, имеющих ограниченное время жизни. Для анализа построена и реализована на языке C# имитационная модель.

Получены соотношения между долей обработанных заявок и количеством каналов обслуживания как для систем с опцией накопления очереди, так и без нее. Проведены эксперименты с ординарным входным потоком заявок с тем же самым набором параметров. Одним из результатов явилось обнаружение «выхода на плато» долей обработанных заявок в процессах с различным количеством элементов в составе группы. Если число каналов становится больше некоторого значения, доля обработанных заявок с приемлемой для практических расчетов погрешностью стремится к значению для ординарного потока. Эта тенденция сохраняется как для СМО с наличием очереди, так и без нее. Для систем с отсутствием ограничения на длину очереди построены зависимости доли обработанных заявок от количества каналов обслуживания.

На основании проведенного исследования можно утверждать, что увеличение числа каналов, начиная с некоторого значения, становится практически неэффективным. Поскольку введение каждого дополнительного канала в состав системы сопряжено с увеличением затрат ресурсов, основной задачей администратора является принятие решения о целесообразности их использования.

Библиографическая ссылка