Введение
Одним из эффективных способов повышения производительности работы производственного оборудования является применение инструментов составления оптимальных производственных расписаний. В результате минимизируются простои оборудования, что приводит к повышению эффективности производства с минимальными финансовыми затратами. Для решения проблемы простоев существуют системы формирования производственных расписаний [1], позволяющие получить некоторый рациональный производственный план. Однако из-за многовариантности и сложности производственных процессов задача развития теории формирования производственных расписаний остается актуальной.
Обзор систем составления производственных расписаний не позволил выявить информацию о применяемых в них алгоритмах [1]. В научной литературе проблеме составления оптимальных производственных расписаний уделяется много внимания как российскими исследователями, так и зарубежными. В одних источниках, например в [2; 3], в качестве метода оптимизации рассматриваются генетические алгоритмы (ГА), в других авторы идут по пути комбинирования нескольких подходов, позволяющих усилить возможности каждого [4]. Анализ публикаций позволил установить, что задача составления производственных расписаний, несмотря на существующие специализированные системы, вызывает высокий интерес, что свидетельствует о наличии нерешенных проблем и обуславливает актуальность исследований в области оптимизации оперативно-календарного планирования. Предложенное в работе [5] решение о модификации алгоритма путем разбиения на исследующий поиск и поиск глобального оптимального значения близко к комбинации эволюционных моделей Дарвина и де Фриза, основанной на совокупности катастроф и глобальных катаклизмов в естественной среде, вызвавших изменения особей и популяций в целом [6, с. 66].
Сама по себе идея комбинирования различных моделей эволюции для решения одной оптимизационной задачи не нова. Так, например, в одной работе описывается совместное использование ГА, основанных на эволюционных моделях Дарвина, Ламарка, де Фриза и Поппера [7, с. 164]. Проведенный авторами вычислительный эксперимент показал, что последовательное применение моделей эволюции Ламарка и де Фриза дало положительный результат, но привело к увеличению объема вычислений [5]. Незначительные изменения популяции, вызываемые оператором мутации, не смогли гарантированно избежать определения локального оптимального производственного расписания. С другой стороны, гипотеза о теории глобальных катаклизмов показала свою эффективность.
Целью исследования является исключение сходимости генетического алгоритма в локальном экстремуме при поиске оптимального производственного расписания.
Материалы и методы исследования
Для того, чтобы увеличить генетическое разнообразие, на начальных этапах поиска оптимального производственного расписания предлагается ввести оператор редукции, который предназначен для устранения выявленных неудачных решений [7, с. 92].
В ряде исследований высокую эффективность показало применение элитной редукции, при которой из популяции исключается n худших особей, а взамен по алгоритму создания популяции случайным образом генерируется такое же количество новых [8–10]. От величины и вероятности редукции напрямую зависит эффективность работы генетического алгоритма. Жестко заданные высокие значения этих параметров не позволят алгоритму сойтись в минимуме, а низкие значения могут не дать ожидаемого разнообразия популяции в момент застревания ГА в локальном оптимуме для выхода к глобальному.
На начальных этапах работы ГА исключение особей из популяции применением последовательного типа редукции, на основе случайного выбора позволит разнообразить популяцию. В процессе эволюции поколений необходимо снижать вероятность выполнения оператора редукции, для обеспечения сходимости ГА. Применение варьируемых значений параметров генетических операторов обычно реализуется на основе математических положений нечеткого логического вывода [11; 12]. Нечеткая логика в основном применяется для настройки операторов кроссовера и мутации [13–15]. В проведенном авторами исследовании предлагается в качестве управляемых значений параметров ГА задать лингвистические переменные NR – Величина редукции и VR – Вероятность редукции. Значение этих переменных зависит от скорости сходимости алгоритма и количества прошедших эпох.
Для переменной Nr – Величина редукции определим универсальное множество UR = [0,50] и терм-множество TR = {низкая, нормальная, высокая}. Для каждого терм-множества зададим функции принадлежности, графики которых приведены на рис. 1, а.
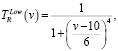 (1)
(1)
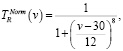 (2)
(2)
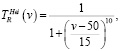 (3)
(3)
где v – количество особей, выбранных для операции редукции.
Здесь и в дальнейшем функции принадлежности и их параметры задавались на основе соответствия ожидаемой логике работы нечеткой операции редукции и корректировались на этапах тестирования и отладки работы программного модуля.
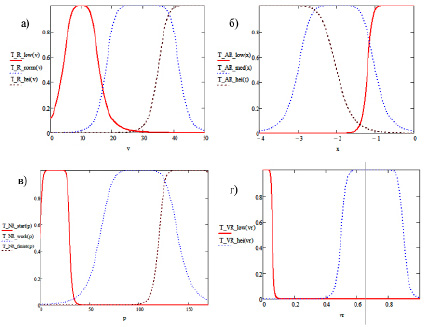
Рис. 1. Графики функций принадлежности терм-множества TR лингвистической переменной Величина редукции: а) терм-множество TR лингвистической переменной Величина редукции; б) терм-множество TAR лингвистической переменной Угол наклона линии тренда; в) терм-множество TNR логистической переменной Количество эпох; г) терм-множество TVR лингвистической переменной Вероятность редукции
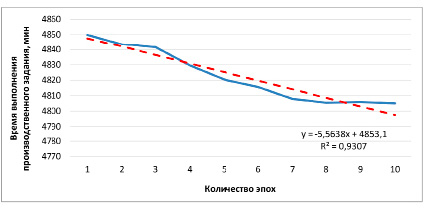
Рис. 2. Пример графика зависимости среднего значения длительности выполнения производственного задания от количества эпох с отображением линии тренда
Значение величины редукции (количества особей, подлежащих замене) зависит от скорости сходимости и количества эпох, выполненных генетическим алгоритмом. Скорость сходимости удобно определить по углу наклона линии тренда графика зависимости среднего значения длительности выполнения производственного задания от количества эпох, пример которого приведен на рис. 2. Первый параметр уравнения линии тренда, представленного на рис. 2, отражает угол наклона и легко определяется с помощью метода наименьших квадратов. В дальнейшем угол наклона линии тренда будем определять по этому параметру.
Зададим лингвистическую переменную AR – Угол наклона линии тренда. Определим для угла наклона универсальное множество UAR = [–4,0] и терм-множество TAR = {низкий, средний, высокий}. Для каждого терм-множества UAR зададим функции принадлежности.
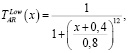 (4)
(4)
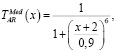 (5)
(5)
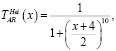 (6)
(6)
где x – угол наклона линии тренда.
Графики описанных функций принадлежности терм-множества логистической переменной Угол наклона линии тренда представлены на рис. 1, б.
Лингвистическую переменную NR – Количество эпох ограничим универсальным множеством UNR = [0,150] и терм-множеством TNR = {начальная, рабочая, финишная}. Для каждого терм-множества TNR зададим функции принадлежности.
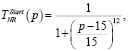 (7)
(7)
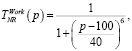 (8)
(8)
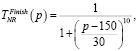 (9)
(9)
где p – количество эпох.
Графики функций принадлежности терм-множества TNR логистической переменной Количество эпох приведены на рис. 1, в.
Наиболее распространенным определением, задающим нечеткое отношение высказывания вида «если А, то В», выявленным японскими математиками Мидзумото, Танака и Фуками, является
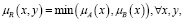 (10)
(10)
где А и В – нечеткие множества на X и Y соответственно;
μR(x,y) – усеченная функция, задаваемая правилами нечеткой базы знаний.
Определим правила, описывающие взаимосвязи между сходимостью алгоритма, количеством эпох и величиной редукции.
1. Если Угол наклона линии тренда «высокий», то Величина редукции «низкая», μ1(x,v).
2. Если Угол наклона линии тренда «средний» и Количество эпох «начальное», то Величина редукции «нормальная», μ2(x,p,v).
3. Если Угол наклона линии тренда «средний» и Количество эпох «рабочее», то Величина редукции «низкая», μ3(x,p,v).
4. Если Количество эпох «финишное», то Величина редукции «низкая», μ4(p,v).
5. Если Угол наклона линии тренда «низкий» и Количество эпох «начальное», то Величина редукции «высокая», μ5(x,p,v).
6. Если Угол наклона линии тренда «низкий» и Количество эпох «рабочее», то Величина редукции «нормальная», μ6(x,p,v).
7. Если Угол наклона линии тренда «низкий» и Количество эпох «финишное», то Величина редукции «высокая», μ7(x,p,v).
Для каждого правила определим усеченные функции принадлежности на основе построения нечеткой импликации в соответствии с (10).
Следующим этапом выполняется процедура аккумуляции, которая определяет функцию принадлежности для всех введенных правил. На этапе аккумуляции могут использоваться функции определения максимума или суммы. Воспользуемся суммированием усеченных функций принадлежности каждого правила:
μ(v) = μ1(x,v) + μ2(x,p,v) + μ3(x,p,v) + μ4(p,v) +
+ μ5(x,p,v) + μ6(x,p,v) + μ7(x,p,v). (11)
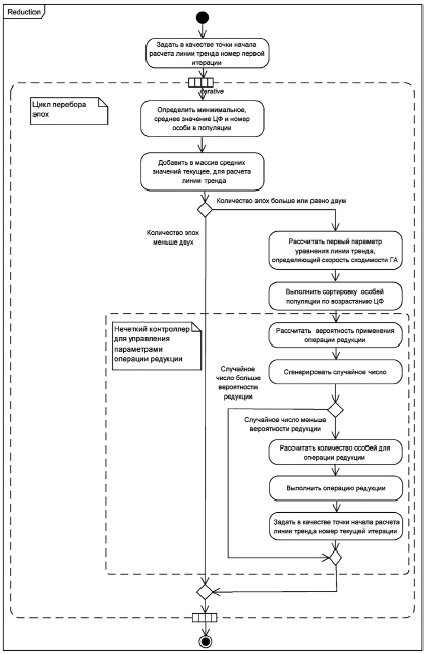
Рис. 3. UML-диаграмма деятельности нечеткой операции редукции
Этап дефаззификации позволяет перейти от нечетких значений переменных к точным значениям. Одним из наиболее популярных методов определения точных значений является вычисление «центра тяжести» функции принадлежности μ(v) для нечеткого значения, полученной на этапе аккумуляции.
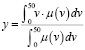 . (12)
. (12)
Вероятность редукции зависит от параметров процесса поиска. На начальных этапах работы генетического алгоритма при высокой сходимости редукция не требуется или может быть применена с минимальной вероятностью и для минимального количества особей. В процессе дальнейшей работы алгоритма вероятность применения операции редукции может увеличиться при схождении ГА к оптимальному, возможно локальному, значению. Тем самым увеличение вероятности применения операции редукции приводит к возмущению процесса поиска оптимального значения и выходу из области локального оптимума.
Для переменной VR – Вероятность редукции определим универсальное множество UVR = [0,1] и терм-множество TVR = {низкая, высокая}. Для каждого терм-множества зададим функции принадлежности.
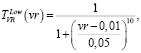 (13)
(13)
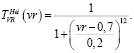 (14)
(14)
где vr – вероятность выполнения операции редукции.
Графики функций принадлежности терм-множества TVR представлены на рис. 1, г.
С учетом (10) определим правила, описывающие зависимость вероятности применения операции редукции от скорости сходимости и количества эпох, пройденных ГА.
8. Если Угол наклона линии тренда «низкий» и Количество эпох «начальное», то Вероятность редукции «высокая», μ8(x,p,vr).
9. Если Угол наклона линии тренда «высокий» и Количество эпох «рабочее», то Вероятность редукции «низкая», μ9(x,p,vr).
Тогда на этапе аккумуляции получим
μvr(vr) = μ8(x,p,vr) + μ9(x,p,vr) (15)
На этапе дефаззификации формула (12) примет вид
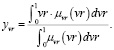 (16)
(16)
Программная реализация нечеткого контроллера для управления параметрами генетического алгоритма
UML-диаграмма деятельности нечеткой операции редукции приведена на рис. 3.
Особенностью реализации является сдвиг начала расчета угла наклона линии тренда после каждого выполнения операции редукции на номер текущего поколения. Рассчитанное значение первого параметра уравнения линии тренда в дальнейшем используется при определении вероятности редукции и при определении количества особей, участвующих в операции редукции. Условием окончания поиска в данном случае является достижение генетическим алгоритмом 150 эпох. Данная реализация предназначена для проведения вычислительных экспериментов, направленных на определение эффективности поиска глобального оптимального производственного расписания. В дальнейшем в качестве условия окончания поиска может выступать близость предыдущего оптимального решения и решения, полученного на текущей итерации алгоритма.
Результаты исследования и их обсуждение
Оценка эффективности поиска оптимального производственного расписания с помощью нечеткого генетического алгоритма выполнялась путем многократного запуска процесса поиска оптимального значения с ведением протокола. Расписание составлялось для шести изделий, четыре из которых должны обрабатываться на трех группах оборудования. Горизонт планирования ограничивается количеством запускаемых изделий в обработку, равным 100 шт. для каждого наименования. Экспериментально был определен глобальный минимум времени выполнения этого производственного задания, который составил 4800 мин.
Результаты экспериментов, при которых генетический алгоритм сразу сходился к глобальному оптимальному значению, отбрасывались, и для обработки оставлялись результаты только тех экспериментов, на которых возникало застревание в локальном экстремуме.
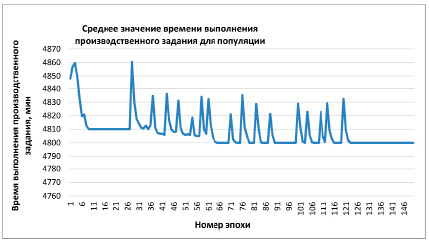
Рис. 4. Фрагмент с результатами процесса поиска оптимального производственного расписания с применением нечеткой редукции
На рис. 4 представлен фрагмент полученных результатов одного из запусков процесса поиска. Из рисунка видно, что на 10 эпохе алгоритм сошелся в локальном оптимуме (модель эволюции Ламарка), составляющем 4810 мин, и не мог выйти из него до момента срабатывания нечеткой редукции (модель эволюции де Фриза, 27 эпоха). Затем было несколько вызовов операции нечеткой редукции, которые внесли существенное разнообразие в сложившуюся популяцию, и алгоритм стал сходиться к другому локальному значению производственного расписания, равному 4805 мин, что хорошо видно на 56 эпохе. Дальнейшая работа нечеткой операции редукции позволила алгоритму достичь глобального минимума на 66 эпохе. После этого видно еще несколько вызовов нечеткой операции редукции, но их действие не привело к выходу из глобального оптимума ни в одном из 30 экспериментов.
Заключение
В результате проведенного исследования получены новые модели, обеспечивающие управление параметрами генетического алгоритма, отличающиеся от известных тем, что определяют величину и вероятность редукции в зависимости от скорости сходимости алгоритма и количества прошедших эпох. Применение предложенных моделей в генетическом алгоритме оптимизации производственного расписания позволило определить глобальный экстремум для всех 30 экспериментов. Ключевым результатом, полученным при использовании нечеткой операции редукции, является выход алгоритма из локального оптимума, который мог определяться в течение нескольких эпох. На практике полученные результаты позволят полностью исключить простои оборудования, возможные в случае составлении локального оптимального производственного расписания.
Библиографическая ссылка
Сергеев А.И., Воронин Д.Н., Корнипаев М.А., Проскурин Д.А. ФОРМИРОВАНИЕ ПРОИЗВОДСТВЕННЫХ РАСПИСАНИЙ ГЕНЕТИЧЕСКИМ АЛГОРИТМОМ С НЕЧЕТКОЙ ОПЕРАЦИЕЙ РЕДУКЦИИ // Современные наукоемкие технологии. 2024. № 10. С. 86-93;URL: https://top-technologies.ru/ru/article/view?id=40176 (дата обращения: 10.03.2026).
DOI: https://doi.org/10.17513/snt.40176



