Введение
В последнее время в связи с переходом на «альтернативные» виды энергетики проточные накопители гибридного типа начали представлять большой интерес. К таким накопителям, например, относятся основанные на парах цинк-воздушные батареи, цинк-никель, цинк-серебро, цинк-кобальт и цинк-марганец.
В связи с необходимости обеспечить бесперебойную подачу энергии с ветровых и солнечных электростанций развиваются такие технологические решения, как проточные накопители. Из-за сравнительной небольшой себестоимости на рынок выходят гибридные накопители на основе цинка. Во время зарядки проточных накопителей при протекании тока на отрицательном электроде выделяется цинк. Во время разрядки этот цинк, наоборот, растворяется в электролите. При этом, как и для всех батарей гибридного типа, время работы определяется площадью поверхности электродов и скоростью разрастания осадка на ней.
Водные цинковые батареи в зависимости от водородного показателя можно разделить на кислые, щелочные и нейтральные. В работе [1] можно найти некоторые варианты составов катода с мягкими водными электролитами для использования с цинковыми анодами и кислыми электролитами. Также в ней приведены общие реакции для марганцевых и кобальтовых батарей. В работе [2] приведена обзорная информация о щелочных цинковых батареях. В качестве достоинства было отмечено, что они обладают высокой энергетической плотностью; были показаны сравнительные характеристики цинковых батарей в зависимости от парного компонента. В обзоре разобраны основные проблемы цинковых батарей, такие как неравномерное осаждение цинка, выделение водорода, пассивация поверхности.
Одним из способов изучения фундаментальных процессов осаждения и растворения цинка является моделирование, которое уменьшает время на подбор параметров для режимов работы разрабатываемых и модифицируемых установок.
Гетерогенные процессы, к которым относится и электролиз, протекают на поверхности раздела сред, при этом их относят к процессам, развитие которых происходит линейно. Однако в силу большого количества факторов, таких как материал электрода, состав электролита, шероховатость поверхности, скорость отвода продуктов реакции и т.д., происходит нарушение линейности изменения характеристик процесса. Так как на поверхности могут протекать параллельные процессы выделения, имеющие несколько веток стадийных электрохимических реакций, то эффективность электролизера можно представить решением «0» – мерных кинетических моделей. Первый подход состоит в поиске коэффициентов по литературным источникам или экспериментальным их определениям. Сложность данного подхода заключается в том, что:
− константы скоростей процессов (коэффициенты уравнений) зависят от большого количества факторов и зачастую применимы только для рассматриваемой системы;
− сложность экспериментального нахождения констант заключается в том, что общая реакция проходит в несколько стадий. При этом каждая стадия может иметь как линейный, так и экспоненциальный характер, выраженный уравнением Аррениуса, и самая медленная из них окажется лимитирующей. Поэтому встает еще одна задача по исследованию вида зависимости для расчета лимитирующей скорости (ведь она может быть как нулевого порядка, так и экспоненциального), а данная задача не является тривиальной.
Целью исследования является установление возможности переноса численного алгоритма исследования прикатодных процессов электролиза, разработанного в приближении неизменности площади электрода для вещества, выделяемого в газовой фазе, на случай осаждения вещества на электроде, приводящего к изменению поверхностных свойств электрода.
Материалы и методы исследования
Гетерогенные процессы, проходящие на границе сред, можно рассматривать в «0»-мерном приближении, если условия однородны на всей поверхности раздела сред. В этом приближении изменений концентрации записываются в виде системы кинетических уравнений, где скорость изменения концентрации по времени равна суммарной скорости увеличения и уменьшения концентрации в результате протекания стадийных химических реакций. Если известны константы скоростей химических реакций, то, как правило, система решается явными или неявными методами семейства Рунге – Кутты в зависимости от свойств системы. Если же скорости неизвестны, то задача перестает быть тривиальной. В данной работе предложен метод, позволяющий решать обратную задачу по имеющимся экспериментальным данным выхода, опираясь на описания протекания химических процессов. С помощью данного алгоритма можно провести расчеты на каждом из электродов. В ходе численных экспериментов вычисляются не только прогнозные значения выхода, но и константы скоростей электрохимических стадийных процессов.
В этой статье метод, представленный в работах [3, 4], исследуется на возможность применения в случае, когда осаждаемый осадок покрывает поверхность электрода и образует пористую пленку, не оказывающую сопротивление реагентам, в модели это учитывается через слагаемые, отвечающие за диффузию через пограничный слой (осадок). Однако в случае наличия добавок, уменьшающих образование дендритов, модель должна быть изменена. Алгоритм, разработанный авторами в работах [5], был видоизменен. Изначально алгоритм сочетал в себе прямой оптимизационный метод и явный метод Рунге – Кутты четвертого порядка. Последний метод был заменен неявным методом Рунге – Кутты из-за того, что общая скорость электроосаждения определяется самой медленной лимитирующий реакцией, а также некоторыми другими параметрами, из-за этого лимитирующий процесс может сместиться в сторону нелинейного характера. Метод Хука – Дживса относится к классу прямых методов, поэтому он основывается на непосредственном вычислении суммы квадратов отклонения просчитанных значений от полученных практически. Также на данный метод накладываются условия неотрицательности для концентраций и констант.
Как было упомянуто выше в связи с тем, что линейность процесса может быть нарушена, для решения прямой задачи использовался неявный метод Рунге – Кутты. Решение системы задач Коши, описывающих изменение концентраций по времени, находится итерационно, начальное приближение взято из состоянии систем:
,
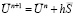где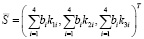 
.
Здесь коэффициенты kj,i находятся из системы нелинейных уравнений
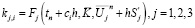
и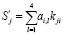 
с помощью метода прямой итерации. Здесь коэффициенты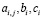 
– числа на соответствующих местах в матрице Бутчера:
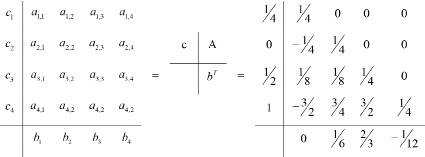
Опишем также метод прямой итерации: зададим начальное приближение kj0 и точность ε. Обозначим:
.
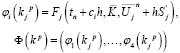Далее находим следующее приближение, как: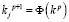 
.
Если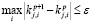 
, то алгоритм заканчивает работу.
Иначе, полагаем p = p + 1 и находим следующее приближение.
Эксперимент, результат которого использовался для верификации данного метода, описан в [6].
Наглядно представлены результаты выщелачивания цинковой руды. В ней измельченная до 150 мкм и прокаленная в течение 2 ч при 400ºС руда помещалась на 4 ч в 20% раствором гидроксида натрия при 100ºС. Затем попавший в электролит свинец осаждался сульфидом натрия. При этом концентрация ионов цинка Zn2+ в приготовленном растворе составляет 10 г/л.
Рабочий электрод был сделан из нержавеющей стали и имеет площадь в 1 см2.
Результаты исследования и их обсуждение
В работе [7] было показано, что в щелочном электролите осаждение цинка проходит через образование и разложение иона тетрогидроксоцинката цинка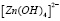 
с одновременным спонтанным выделением водорода.
В работе [8] показано, что пороговое значение концентрации раствора гидроксида натрия достаточное для существования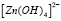 
это 20 %. При уменьшении концентрации выделение цинка происходит через его оксид. Однако при определенных условиях возможно загрязнение цинкового покрытия гидроксидом цинка [9], но так как в большинстве работ это не наблюдается, то в данной работе этот случай не рассматривается.
Таким образом, процесс растворения цинкосодержащей руды в 20% растворе NaOH опишем как
.
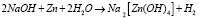При электроэкстракции спонтанное выделение водорода приводит к водородной хрупкости металла [10; 11, с. 351–352]. Однако преобладает мнение, что прямой связи между этими конкурирующими реакциями нет, поэтому для примера возьмем только те стадийные реакции, которые описывают электроосаждение цинка [12].
Тогда процесс осаждения цинка можно описать следующей системой:
,
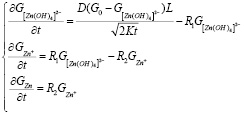где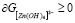 
, 
, 
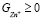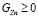– концентрация ионов тетрагидроксоцинката, ионов цинка и концентрация цинка соответственно, R1 и R2 – константы скоростей реакций. Также введем K – константу пропорциональности между толщиной пористой пленки осадка и времени из уравнения Яндера и L – коэффициент пропорциональности диффузионного потока 
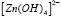через пористый слой.
Данная математическая модель построена в предположении пористости осадка, что в целом находит подтверждение при исследовании образования дендритов [13, 14].
Для перевода вычисленной концентрации в массу пленки используем следующую формулу:
,
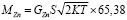где T – время, на которое существуют экспериментальные значения. Здесь считается, что выполняется уравнение Яндера.
Результаты работы сравнивались с экспериментальными данными работы [6] и [5], при плотности тока 125 А/м2 и расчетными данными работы [5]. Для начала расчетов из условий эксперимента [6] и уравнения реакции растворения цинкосодержащей руды примем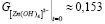 
моль/л, 
, 
.
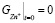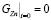Условия на скорости процессов задаются согласно соотношению, связывающему лимитирующую скорость реакций и соответствующие стехиометрические числа. Результаты вычислений приведены в таблице.
Сравнение данных при плотности тока 125 А/м2
|
Временной шаг, мин |
Эксперимент [6], г |
Расчет, г |
Расчет [5], г |
|
20 |
0,467–0,49 |
0,30 |
0,30115 |
|
40 |
0,976–1,03 |
0,56 |
0,8516 |
|
60 |
1,4945–1,6 |
1,55 |
1,564 |
Расчеты показали большую погрешность в начальной стадии развития процесса, когда образование дендритов цинка сильно нарушает линейность процесса, в силу того, что процессы проходят с разной скоростью на стальном электроде и зародыше цинка. Здесь результаты вычислений показали необходимость учета процессов выделения водорода, несмотря на кажущуюся независимость параллельных реакций. В работе [15] предположено, что возможны реакции перезарядки, то есть обмен электронами, между ионами цинка и атомами водорода, а также ионами водорода и атомами. Также может иметь место установление линейности процесса с течением времени. В начале, когда только начинается зародышеобразование, выделение цинка проходит с разной скоростью на неравномерной поверхности электрода, и происходит нарушение линейности процесса. В работе [13] для кислого электролита в цинк ионной батареи была исследована зависимость между плотностью зародышеобразования, плотностью тока и пропускной способностью емкости и было показано, что чем выше плотность тока, тем выше плотность ядер и тем меньше размер образованных ядер у зародышей. Можно предположить существование аналогичных зависимостей для щелочных электролитов. В работе [16] отмечено, что использование цинковых батарей затрудняется образованием дендритов. Для решения этой проблемы было предложено использование добавок к основному электролиту для обеспечения более равномерного осаждения. Однако в научной литературе обычно отмечается, что при обратном растворении цинка могут возникнуть затруднения, если использовать для более равномерного осаждения цинка катализаторы. Так, в обзоре [17] отмечено, что проблема однородности осадка еще не решена и ее решение должно быть комплексным и заключаться в модифицировании самой поверхности электродов и нахождении легкодоступных добавок к электролиту.
Заключение
В данной работе рассматривается возможность переноса численного алгоритма исследования прикатодных процессов электролиза, разработанного в приближении неизменности площади электрода для вещества, выделяемого в газовой фазе, на случай осаждения вещества на электроде, приводящего к изменению поверхностных свойств электрода. Алгоритм, в отличие от известных статистических методов, например построения регрессионных моделей или методов интерполяции, позволяет определить прогнозные значения массы цинка при меньшем количестве экспериментов не просто в виде функциональной зависимости с подгоночными коэффициентами, а непосредственно оценить вклады электрохимических процессов, выделить лимитирующую реакцию, непосредственно опираясь на теорию электрохимических процессов.
Результаты расчетов на примере электроосаждения цинка показали большую погрешность в начальный период процесса, где происходит рост дендритов цинка, и уменьшение погрешности с увеличением времени протекания процесса, таким образом алгоритм можно использовать для прогнозирования выделения на больший временной отрезок, непосредственно на начальный период в математической модели необходимо учесть влияние водорода и сильную неоднородность поверхности, формирующуюся за счет роста дендритов.
Библиографическая ссылка
Дмитриев М.С., Кашапов Н.Ф., Чебакова В.Ю., Кормушин К.В. МОДЕЛИРОВАНИЕ ВЫДЕЛЕНИЯ ЦИНКА В НАКОПИТЕЛЯХ ГИБРИДНОГО ТИПА // Современные наукоемкие технологии. – 2024. – № 10. – С. 44-48;URL: https://top-technologies.ru/ru/article/view?id=40170 (дата обращения: 21.11.2024).