Введение
Пористые материалы получили широкое распространение в строительстве – они используются для создания легких бетонов и пенополистирола [1, 2]; в космическом и авиационном машиностроении пористые материалы применяются для изготовления теплоизоляционных материалов и снижения веса конструкций [3]; в энергетике применяются при изготовлении теплообменных трактов теплообменных устройств [4–6], как рабочая зона фильтров, сепараторов и др. [7].
В настоящей работе рассматриваются пористые материалы c упорядоченной структурой на основе трижды периодических минимальных поверхностей (ТПМП-материалы). Подобные материалы представляют особый интерес, так как обладают прогнозируемыми физическими свойствами и уникальной макроструктурой. Так, например, в материалах на основе ТПМП можно организовать систему двух и более непересекающихся поровых объемов, что делает возможным их использование в качестве теплообменных трактов ТМО-оборудования. Кроме того, каркасы ТПМП-материалов обладают развитой поверхностью, что оказывает положительное влияние на теплоотдачу (при течении жидкостей и газов через поровое пространство) и теплопроводность материала.
Все ТПМП-материалы состоят из твердотельного каркаса, образованного элементарными ячейками Фишера – Коха и пор, которые образуют сложную систему каналов, полостей. Поровое пространство может быть заполнено воздухом, жидкостями, газами и другими наполнителями. Особенность ТПМП-материалов состоит в том, что их свойства, в том числе теплофизические, непосредственно связаны с геометрическими характеристиками элементарных ячеек (толщиной стенки, размером и др.). Таким образом, изменяя геометрические характеристики и материал наполнителя, можно получить требуемые физические свойства пористой среды.
Изучение свойств материалов с пористой структурой представляет как теоретический, так и прикладной интерес [8]. Несмотря на очевидные преимущества материалов с прогнозируемыми свойствами, существует ряд факторов, ограничивающих их применение: технологические и технико-экономические ограничения аддитивного производства; сложность моделирования процессов, протекающих в пористых средах, и проектирования устройств на их основе [9–11]. В работах [12–14] приведены результаты экспериментальных и аналитических исследований процессов переноса в ТПМП типа Шена и IWP. Настоящая статья посвящена исследованию процесса переноса тепла в пористом материале на основе элементарной ячейки типа Фишера – Коха S. Представленный алгоритм получения решения может быть использован и для других типов ячеек, допускающих осреднение свойств в пределах исследуемого объема, то есть использование эффективных характеристик вместо истинных. Особенности использования разработанного приближенно-аналитического метода рассмотрены на примере решения краевой задачи теплопроводности в тонкой пластине.
Цель исследования – изучение процесса теплопроводности в пористой пластине с ТПМП-топологией и внутренним источником теплоты, учитывая геометрические характеристики ячейки.
Материалы и методы исследования
В настоящей работе рассмотрена задача теплопроводности в пластине с топологией ТПМП типа Фишера – Коха S. Внутри пластины толщиной 2l действует распределенный объемный источник теплоты, а на поверхности заданы симметричные граничные условия третьего рода (рис. 1).
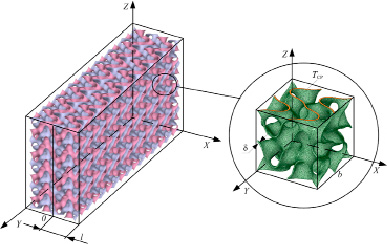
Рис. 1. Графическое представление трехмерной модели пористой пластины
Емкостные свойства среды характеризуются пористостью φ, определяемой выражением [13]:
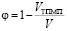 , (1)
, (1)
где VТПМП – объем элементарной ячейки; V – объем куба, в который вписана ячейка.
Пористость элементарной ячейки φ зависит от геометрических параметров (толщины стенки ячейки δ и длины ребра куба b, в который вписана ячейка (рис. 1)) и определяется стандартными средствами модуля SpaceClaim программного комплекса ANSYS. Аппроксимируя полученные результаты в ANSYS, получаем выражение
φ = 1 – 5,0735 ∙ Δ, (2)
где Δ – относительная толщина, Δ = δ / b.
Математическая постановка задачи с учетом симметрии имеет вид
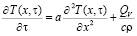 ,
,
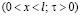 ; (3)
; (3)
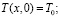 (4)
(4)
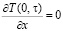 ; (5)
; (5)
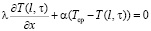 , (6)
, (6)
где T – температура; Tcp – температура среды; T0 – начальная температура; QV – объемная мощность внутреннего источника тепла; x – координата; α – коэффициент теплоотдачи; ρ – плотность; τ – время; λ – коэффициент теплопроводности; a = λ / (cρ) – коэффициент температуропроводности; ρ – плотность; c – удельная теплоемкость; l – половина толщины пластины; λ – коэффициент теплопроводности.
В соответствии с задачей (3)–(6) на одной из граней исследуемой ячейки задается граничное условие третьего рода Tcp, а на всех остальных – отсутствие теплообмена.
С помощью метода минимального репрезентативного объема [12] была выполнена вычислительная «гомогенизация среды», направленная на осреднение теплофизических характеристик материала.
Согласно данному методу, представленному в работе [12], уравнение (3) примет вид
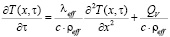 , (7)
, (7)
где ceff (ceff = c), ceff , λeff – эффективные (осредненные) коэффициенты теплоемкости, плотности, теплопроводности гомогенизированной среды.
Эффективная плотность материала ρeff определяется как
ρeff = ρs ∙ (1 – φ), (8)
где ρs – истинное значение плотности материала каркаса, из которого изготовлена пористая ячейка.
Эффективный коэффициент теплопроводности λeff определяется следующей зависимостью:
λeff = λs ∙ 0,73 ∙ (1 – φ), (9)
где λs – коэффициент теплопроводности материала твердотельного каркаса [14].
С учетом (8) и as = λs / (cρs) запишем
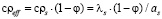 , (10)
, (10)
С учетом (10) уравнение (3) можно представить как
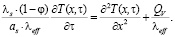 (11)
(11)
Выполним параметризацию уравнения (3). Введем следующие параметры:
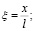
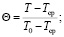
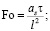
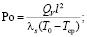
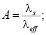
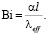
где Θ – безразмерная температура; ξ – безразмерная координата; l – линейный размер ячейки, м; Fo – безразмерное время (критерий Фурье); Po – критерий Померанцева; A – коэффициент, зависящий от тепловых свойств материала твердотельного каркаса и эффективного коэффициента теплопроводности.
Уравнение (3) в безразмерном виде можно записать (рис. 3) как
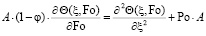
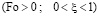 ; (12)
; (12)
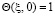 ; (13)
; (13)
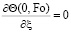 ; (14)
; (14)
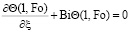 . (15)
. (15)
Для решения задачи (12)–(15) используется метод, предложенный авторами в [15].
Введем в рассмотрение новую искомую функцию времени
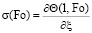 , (16)
, (16)
где α – угол между касательной к графику функции Θ(ξ,Fo) в точке ξ = 1 и координатной осью.
Возвращаясь к размерным величинам, выражение (9) можно представить в виде
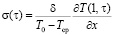 . (17)
. (17)
Плотность теплового потока по закону Фурье на поверхности пластины определяется выражением
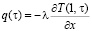 , (18)
, (18)
Подставляя (11) в (10), получаем
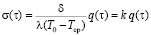 , (19)
, (19)
где k = const – некоторый коэффициент, определяемый масштабом системы.
Решение задачи (5)–(8) представим в виде полинома n-й степени:
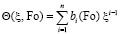 , (20)
, (20)
где 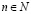 – натуральное число, соответствующее количеству членов ряда (20); bi(Fo) – неизвестные коэффициенты, зависящие от безразмерного времени.
– натуральное число, соответствующее количеству членов ряда (20); bi(Fo) – неизвестные коэффициенты, зависящие от безразмерного времени.
Для получения решения исходной задачи (12)–(15) в первом приближении ограничимся тремя слагаемыми (n = 3) в выражении (20). Выполнив подстановку граничных условий (13)–(15) в полином n-й степени (20), получим систему трех алгебраических уравнений с коэффициентами bi(Fo). Система имеет следующий вид:
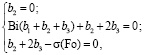
Решая систему, находим коэффициенты:
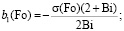
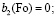
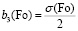 .
.
С учетом полученных коэффициентов полином (20) запишется в виде
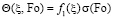 , (21)
, (21)
где 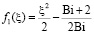 – функция, зависящая от координаты. Найденная функция удовлетворяет граничным условиям (13)–(15) при любых значениях σ(Fo).
– функция, зависящая от координаты. Найденная функция удовлетворяет граничным условиям (13)–(15) при любых значениях σ(Fo).
Проинтегрируем его в пределах изменения пространственной координаты, то есть составим интеграл теплового баланса [9, 10]:
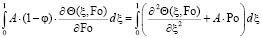 . (22)
. (22)
Вычисляя интеграл, получаем обыкновенное дифференциальное уравнение вида
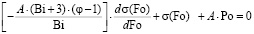 , (23)
, (23)
из решения, которого находим
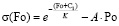 , (24)
, (24)
где C1 – константа интегрирования, 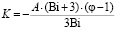 .
.
Подставляя (24) в (21), получаем
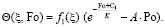 (25)
(25)
Для выполнения начального условия (13) потребуем ортогональности невязки к координатной функции f1(ξ) и составим его невязку:
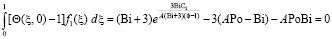 . (26)
. (26)
Из решения уравнения (26) определим константу интегрирования
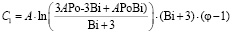 .
.
Выражение (25) с учетом найденной константы С1 представляет собой решение задачи (12)–(15) в первом приближении.
Результаты исследования и их обсуждение
Графики изменения безразмерной температуры по формуле (19) при Bi = 10; Po = 0,005; A = 25,4; φ = 0,95 представлены на рис. 2, 3.
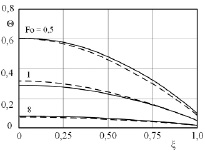
Рис. 2. График распределения температуры в пластине по безразмерной координате: ––––– – приближенное решение (MathCAD), – – – – метод конечных элементов (ANSYS)
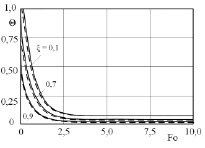
Рис. 3. График распределения температуры в пластине по безразмерному времени: ––––– – приближенное решение (MathCAD), – – – – метод конечных элементов (ANSYS)
Графики изотерм и изменения скоростей движения изотерм представлены на рис. 4, 5. На поверхности тела в определенный момент времени появляется каждая из изотерм, имеющая начальную скорость υ0. Затем скорости изотерм под воздействием постоянного во времени источника Po = 0,0005 стремятся к бесконечным значениям.
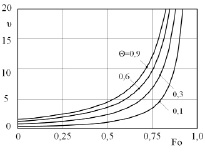
Рис. 4. График распределения скоростей изотерм в пластине при граничных условиях 3-го рода
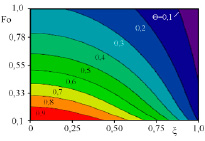
Рис. 5. График распределения изотерм в пластине из пористого материала
Заключение
Было проведено сопоставление результатов расчетов первого приближения температурной функции, полученных приближенно-аналитическим методом и методом конечных элементов, с целью проверки приближенно-аналитического метода решения задачи теплопереноса в пористой среде, основанной на структуре ТПМП типа Фишера – Коха S. Полученные выражения для определения функции температуры позволяют определять распределение тепла внутри пористых материалов, выявлять тепловые потери и др. Решение задачи переноса тепла через плоскую пористую стенку можно получить в простой аналитической форме, не прибегая к специализированному программному обеспечению и вычислительной технике.
В диапазоне времени 0,1 ≤ Fo < ∞ погрешность при вычислениях в первом приближении не более 4% от численных методов. Определение эффективной теплопроводности пористых материалов на основе ТПМП, температурных полей и тепловых потоков внутри пористых сред при одномерном переносе тепла может быть проведено на основе полученных результатов.
Библиографическая ссылка
Губарева К.В., Еремин А.В. ИССЛЕДОВАНИЕ ТЕПЛОПРОВОДНОСТИ ПОРИСТЫХ МАТЕРИАЛОВ СО СТРУКТУРОЙ ТИПА ФИШЕРА – КОХА S // Современные наукоемкие технологии. 2024. № 10. С. 38-43;URL: https://top-technologies.ru/ru/article/view?id=40169 (дата обращения: 10.03.2026).
DOI: https://doi.org/10.17513/snt.40169



