Введение
В процессе строительства верхних слоев асфальтобетонных (АБ) покрытий автомобильных дорог происходит формирование готового объекта. Качество покрытия зависит от эффективности процессов укладки и уплотнения горячей АБ смеси. До 50 % дефектов будущей эксплуатации АБ покрытий зависит от равномерности уплотнения АБ смеси во время строительства. Обеспечение этого фактора является научно-технической проблемой из-за высокой сложности процессов взаимодействия рабочих органов дорожных машин (ДМ) и АБ смеси, а также необходимости повышения производительности строительства при нормативном качестве дорожных покрытий.
Возможным решением проблемы обеспечения равномерной плотности АБ смеси по всей ширине автомобильной дороги во время строительства является усовершенствование технологического процесса на базе использования автоматизированных ДМ с элементами интеллектуального управления ими [1].
Методология, теоретические основы построения интеллектуальной системы автоматического контроля (САК) плотности для асфальтоукладчиков (АУ) и дорожных катков рассмотрена в авторских работах [2, 3]. Методы усовершенствования систем управления плотностью АБ смесей на базе киберфизической системы, применение более эффективной технологии строительства и использования автоматизированных АУ и дорожных катков рассмотрены в работе [4].
Цель исследования – построение модели интеллектуальной системы автоматического контроля плотности АБ смеси для укладчиков.
В работе рассматривается задача построения САК плотности на базе технологии вычислительного интеллекта – нечеткой нейронной сети, для повышения производительности уплотнения и равномерности плотности АБ смеси по всей ширине автомобильной дороги во время укладки смеси с учетом заданных в проекте производства работ значений показателей качества.
Материалы и методы исследования
Базовой информацией являются данные переменных, полученные учеными ВНИИСДМ, СоюзДорНИИ и др., а также определенные автором с соавторами в результате полевого экспериментального исследования в пригороде Красноярска осенью 2021 г.
В рабочем процессе АУ обеспечивает распределение смеси по ширине рабочего органа, уплотнение и нивелирование поверхности заданного профиля и толщины. Современные АУ с рабочим органом, состоящим из трамбующего бруса (ТБ), вибрационной плиты, прессующих планок, в процессе уплотнения обеспечивают деформирование АБ смеси, при этом уплотненность по всей ширине рабочего органа завершается за 4÷6 ударов ТБ. Особенностью процесса укладки АБ смеси АУ является то, что вибрационная плита рабочего органа, находясь в постоянном контакте с поверхностью смеси, обеспечивает структурное улучшение однородности слоя смеси. В зависимости от динамических вибропараметров рабочего органа АУ и физико-механических характеристик АБ смеси амплитуда, скорость и ускорение колебаний виброплиты непрерывно изменяются. В работах [5–7] авторы рассматривали задачу построения интеллектуальной САК плотности АБ смеси на базе нейросетевых структур.
Входные переменные. Переменные, определяемые на основе сигналов акселерометра, – показатели во временной области, показатели ICMVs в частотной области: CMV; CCV; THD; AICV; ICV; MFD [8–10].
Выходная переменная. Обычно после прохода АУ остается уплотненное АБ покрытие, которое характеризуется плотностью АБ смеси. Она зависит от количества циклов трамбующих ударов, времени действия вибрационной нагрузки, а также скорости изменения напряженного состояния [11]. Заданную плотность можно обеспечить при настройках определенных значений режимных параметров АУ и дорожных катков, которые будут соответствовать физико-механическим свойствам уплотняемого материала. Выходной переменной системы является значение степени уплотнения АБ смеси, которая является достаточно информативной и определяет основное назначение будущего дорожного покрытия автомобильной дороги.
Постановку задачи построения системы автоматического контроля плотности смеси для АУ формально предложено представить в виде следующих функциональных зависимостей:
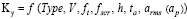 , (1)
, (1)
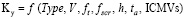 , (2)
, (2)
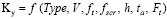 , (3)
, (3)
где Type – индекс типа смеси; V – скорость движения, м/мин; ft – частота колебаний бруса, Гц; fscr – частота колебаний плиты, Гц; h – толщина слоя смеси, м; ta – температура поверхности смеси, oC; arms – среднеквадратичное значение (СКЗ) ускорения плиты, м/с2; ap – максимальное абсолютное значение ускорения, м/с2; ICMVs – показатели интеллектуального уплотнения; Ft – усилие в толкателе бруса, кН.
Анализ переменных Type, V, ft, fscr, h, ta, ap, arms, Ft, ICMVs, представленных в моделях (1)–(3), показал хорошую корреляционную связь с плотностью асфальтобетонной смеси [12].
Использование интеллектуальной САК для АУ, построенной на базе моделей (1)–(3), за счет обеспечения высокой плотности АБ смеси по всей ширине рабочего органа АУ, позволит уменьшить количество применяемых в технологическом процессе дорожных катков, сократить время работы звена ДМ при уплотнении АБ смеси и, следовательно, повысить производительность процесса уплотнения [12].
Предложено построение интеллектуальной САК плотности выполнить на базе гибридной нейронечеткой сети (ГННС). Они обладают достоинствами искусственных нейронных сетей (ИНС) прямого распространения (ПР) к обучению, а также хорошему объяснению выводов нечеткой логики. Недостатком ИНС является необходимость большого количества данных переменных для ее обучения.
В ГННС используется нечеткая логика, которая позволяет строить имитационные модели для условий неопределенности, а также недостатка исходных данных переменных [13]. В работе [14] рассмотрены особенности более десятка разновидностей ГННС: НИНС Такаги – Сугэно – Канга (TSK), Ванга – Менделя (VM), адаптивная НИНС ANFIS и др. Архитектуры сетей НИНС ANFIS (англ. Adaptive-Network-Based Fuzzy Inference System) и GARIC (англ. Generalized Approximate Reasoning-based Intelligence Control) используют в системах управления [14].
Предложено исследовать использование ГННС типа ANFIS в качестве прогнозирующей модели САК плотности АБ смеси. Сеть ANFIS имеет структуру пятислойной ИНС ПР с нечеткой моделью вывода типа Такаги – Сугэно (TS).
Постановка задачи. Построить модель интеллектуальной САК плотности АБ смеси на базе ГННС MISO-типа, с учетом предложенных обоснованных вариантов моделей (рис. 1), отличающихся данными переменных вектора входного слоя сети ANFIS.
Предложен алгоритм синтеза модели ГННС САК плотности АБ смеси для АУ в среде программы MATLAB/Simulink.
Шаг 1. Накопление и предобработка (нормирование) набора данных переменных.
Шаг 2. Задание структуры ГННС САК плотности.
Шаг 3. Запуск ANFIS редактора.
Шаг 4. Загрузка обучающей выборки (файл *.dat).
Шаг 5. Построение исходной системы нечеткого логического вывода.
Шаг 6. Обучение модели ГННС типа ANFIS.
Шаг 7. Тестирование модели ГННС САК плотности.
Шаг 8. Сохранение файла (расширение *.fis.) модели построенной системы.
Шаг 9. Имитационное моделирование ГННС САК. Анализ результатов.
В программной среде MATLAB для системы типа ANFIS реализованы 8 функций принадлежности (ФП): треугольная (trimf); трапециевидная (trapmf); колоколообразная (gbellmf); гауссова и двухсторонняя гауссова (gaussmf и gauss2mf); Пи-образная функция (pimf); разность и произведение двух сигмоидных функций (dsigmf и psigmf).
Сеть ANFIS содержит два типа ФП выходных переменных: константа (constant, нулевой порядок); линейная (linear, первый порядок). Применено нормирование (масштабирование) входного вектора ГННС.
Для создания ГННС MISO системы в программной среде MATLAB/Simulink используется команда anfisedit.
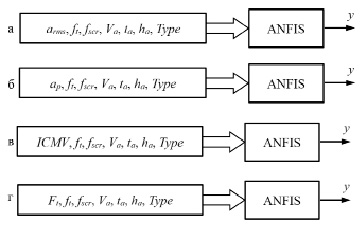
Рис. 1. Варианты модели ГННС САК плотности для АУ : а – 1; б – 2; в – 3; г – 4
Формирование набора данных переменных, использованных во входных векторах ГННС, строилось на базе результатов измерений сигналов акселерометром, установленным на вибрационную плиту АУ, в полевом экспериментальном исследовании в условиях строительства верхнего АБ слоя дорожного покрытия автомобильной дороги. Данные переменных были поделены на обучающую и тестовую выборки в долях 75 % и 25 % соответственно. В табл. 1–4 представлены отрывки обучающих выборок, правый столбец – выходная переменная.
Буква N в индексах переменных (табл. 1–4) указывает на их нормированное значение, масштабированное к интервалу [-1, 1]. Поэтому они имеют как положительные, так и отрицательные значения.
В алгоритме способа нечеткие правила генерируются методом решетчатого разбиения. В исследовании для всех вариантов моделей ГННС типа ANFIS переменные определялись треугольными, трапециевидными, колоколообразными, гауссовыми и двухсторонними гауссовыми ФП. Обучение ГННС выполнялось гибридным методом. Оптимальная модель ANFIS определяется на основе метрики RMSE (англ. Root Mean Squared Error) – среднеквадратическая ошибка.
Таблица 1
Фрагмент обучающей выборки (для варианта модели 1)
|
ft.N, Гц |
arms, м/с2 |
Ку |
|
-0,5 |
1,127 |
0,921 |
|
-0,5 |
0,934 |
0,922 |
|
-0,5 |
0,937 |
0,921 |
|
-0,5 |
0,915 |
0,925 |
|
-0,5 |
1,023 |
0,917 |
|
-0,5 |
1,135 |
0,921 |
Таблица 2
Фрагмент обучающей выборки (для варианта модели 2)
|
ft.N, Гц |
ap, м/с2 |
Ку |
|
-0,5 |
-0,227 |
0,921 |
|
-0,5 |
-0,254 |
0,922 |
|
-0,5 |
-0,342 |
0,921 |
|
-0,5 |
-0,309 |
0,925 |
|
-0,5 |
-0,306 |
0,917 |
|
-0,5 |
-0,128 |
0,921 |
Таблица 3
Фрагмент обучающей выборки (для варианта модели 3)
|
ft.N, Гц |
THDN |
Ку |
|
-0,5 |
0,410 |
0,913 |
|
-0,5 |
0,123 |
0,918 |
|
-0,5 |
0,420 |
0,918 |
|
-0,5 |
0,057 |
0,920 |
|
0,5 |
-0,307 |
0,931 |
|
0,5 |
-0,340 |
0,932 |
Таблица 4
Фрагмент обучающей выборки (для варианта модели 4)
|
TypeN |
ft.N, Гц |
Ft.N, кН |
Ку |
|
-0,5 |
-0,5 |
-0,23 |
0,93 |
|
-0,5 |
-0,378 |
0,34 |
0,97 |
|
-0,5 |
-0,133 |
0,49 |
0,99 |
|
-0,5 |
-0,357 |
-0,29 |
0,91 |
|
-0,167 |
-0,5 |
-0,40 |
0,80 |
|
-0,167 |
-0,378 |
-0,37 |
0,85 |
Результаты исследования и их обсуждение
Модель ННС ANFIS1Paver. Две переменные входного слоя: частота трамбования бруса ft, СКЗ ускорения вибрационной плиты arms, три ФП. После генерации структура системы нечеткого вывода содержит 9 нечетких правил. Результаты обучения модели ГННС типа ANFIS представлены в табл. 5. При использовании двухсторонней гауссовой (gauss2mf) ФП получена лучшая точность – RMSE = 0,002685.
Процедура построения ГННС ANFIS1Paver в среде программы MATLAB при использовании треугольной ФП представлена на рис. 2 и 3.
Проверка адекватности построенных моделей ГННС типа ANFIS в среде программы MATLAB/Simulink выполняется в окне Rule Viewer (рис. 4).
Последовательность проверки заключается во вводе значений исходных данных переменных и автоматическом расчете результата выходной переменной. Визуализация графической поверхности нечеткого вывода для первой ft и второй arms входных переменных 1-й модели представлена на рис. 5.
При построении модели системы на основе ГННС необходимо учитывать особенность, связанную с ограничением прогнозирования в исследованных диапазонах переменных. Для расширения диапазона переменных таких вариантов моделей необходимо сформировать расширенный набор переменных и проводить обучение по приведенной в настоящей работе методике. Обучаемость ГННС типа ANFIS является существенным достоинством для обоснованного выбора при построении систем автоматического управления.
Таблица 5
Структурная информация ANFIS1Paver
|
Тип параметров ANFIS |
ANFIS1Paver (1) |
ANFIS1Paver (2) |
ANFIS1Paver (3) |
ANFIS1Paver (4) |
ANFIS1Paver (5) |
|
Количество входных переменных |
2 |
||||
|
Тип ФП |
треугольная (trimf) |
трапециевидная (trapmf) |
колоколо-образная (gbellmf) |
гауссова (gaussmf) |
гауссова двухсторонняя (gauss2mf) |
|
Тип выходной ФП |
линейная (linear) |
||||
|
Количество ФП входного слоя |
3*3 |
||||
|
Обучающая выборка |
123 |
||||
|
Тестовая выборка |
41 |
||||
|
Количество эпох |
4 |
2 |
60 |
28 |
19 |
|
Количество узлов |
35 |
35 |
35 |
35 |
35 |
|
Количество линейных параметров |
27 |
27 |
27 |
27 |
27 |
|
Количество нелинейных параметров |
18 |
24 |
18 |
12 |
24 |
|
Общее количество параметров |
45 |
51 |
45 |
39 |
51 |
|
Количество нечетких правил |
9 |
9 |
9 |
9 |
9 |
|
Комбинация входа |
ftN, armsN |
||||
|
RMSE |
0.002799 |
0.002786 |
0.002694 |
0.002714 |
0.002685 |
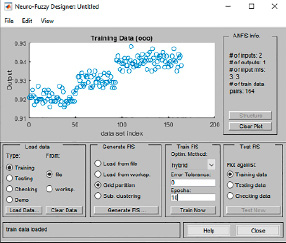
Рис. 2. Вид ANFIS редактора после загрузки обучающих данных
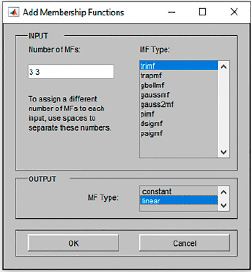
Рис. 3. Выбор количества и типа ФП
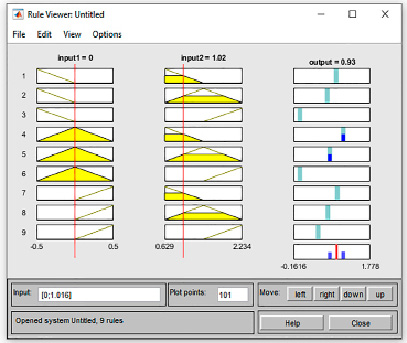
Рис. 4. Просмотр правил сгенерированной системы нечеткого вывода
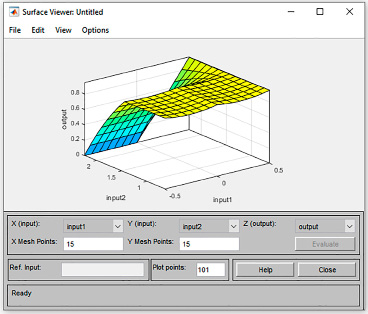
Рис. 5. График поверхности нечеткого вывода модели для первой ft и второй arms переменных
Таблица 6
Результаты имитационного моделирования ГННС типа ANFISiPaver
|
Модель ANFISiPaver |
Переменные входного вектора |
Функция принадлежности |
RMSE |
Относительная ошибка тестовой выборки (максимальное значение), % |
|
ANFIS1Paver(5) |
ft, arms |
двухсторонняя гауссова (gauss2mf) |
0,002685 |
0,54 |
|
ANFIS2Paver(4) |
ft, ap |
гауссова (gaussmf) |
0,002765 |
0,43 |
|
ANFIS3Paver(3) |
ft, THD |
колоколообразная (gbellmf) |
0,002952 |
0,64 |
|
ANFIS4Paver(4) |
Type, ft, Ft |
гауссова (gaussmf) |
0,01272 |
4,09 |
Аналогично найдены решения для 2, 3 и 4-й моделей.
В результате исследования получены 4 оптимальные модели ГННС типа ANFIS, имеющие различные переменные во входном слое. Все варианты предложенных ГННС типа ANFIS показали хорошую или удовлетворительную точность. Проведено моделирование полученных вариантов ГННС на базе тестовых примеров в среде программы MATLAB. Определены относительные ошибки результатов моделирования. Результаты моделирования приведены в табл. 6.
Максимальные значения относительной ошибки для моделей ГННС ANFIS1Paver(5), ANFIS2Paver(4), ANFIS3Paver(3) меньше 1 %, для модели ANFIS4Paver(4) – 4,09 %, что соответствует удовлетворительной адекватности модели.
Концепция построения модели интеллектуальной САК плотности на базе моделей ННС ANFIS позволяет устранить недостатки использования нейросетевых структур.
Заключение
Таким образом, решена задача построения модели интеллектуальной ГННС САК плотности АБ смеси для укладчика. Новизна подхода заключается в предложенных четырех новых моделях интеллектуальных САК плотности.
В результате численного моделирования в среде программы MATLAB/Simulink построенных вариантов моделей ГННС САК показано, что обеспечивается достоверность результата при оценке плотности АБ смеси с относительной ошибкой меньше 5 %.
Использование интеллектуальной САК плотности для АУ позволит повысить производительность процесса уплотнения АБ смесей, а также обеспечить улучшение качества АБ дорожных покрытий автомобильных дорог и объектов транспортной инфраструктуры автомобильного транспорта. Результаты такого улучшения позволят обеспечить ресурсосбережение при строительстве автомобильных дорог на основе уменьшения (оптимизации) количества катков и их типов в звене ДМ, а также увеличения срока службы АБ покрытий при их эксплуатации.
Библиографическая ссылка
Прокопьев А.П., Большаков А.А. РАЗРАБОТКА МОДЕЛИ СИСТЕМЫ КОНТРОЛЯ С НЕЙРОНЕЧЕТКИМ ПРОГНОЗИРОВАНИЕМ ПЛОТНОСТИ АСФАЛЬТОБЕТОННОЙ СМЕСИ ДЛЯ УКЛАДЧИКОВ // Современные наукоемкие технологии. 2024. № 9. С. 36-43;URL: https://top-technologies.ru/ru/article/view?id=40145 (дата обращения: 14.02.2026).
DOI: https://doi.org/10.17513/snt.40145



