Введение
В настоящее время в различных иерархических системах управления – государственных информационных системах, системах управления транспортной отрасли, управляющих подсистемах силовых ведомств, автоматизированных банковских контролирующих системах, автоматизированных системах управления технологическими производственными процессами – возникла необходимость реконфигурации систем математического обеспечения и дооснащения систем защиты информации. Важность оперативного создания дополнительных программно-аппаратных средств, например систем предупреждения несанкционированного доступа (СПНД), обусловлена продолжающимися санкционными воздействиями и неопределенностью содержания их дальнейшего генерирования (количество точечных запретов для отечественных IT-организаций превысило второй десяток). Разработка, испытания и развертывание СПНД должны быть осуществлены в кратчайшие сроки, в связи с этим возникает задача оптимизации расхода ресурсов, привлекаемых к обеспечению выполнения вышеупомянутых проектов. Ее решение, в соответствии с принципом декомпозиции, может включать решение двух взаимосвязанных задач – ситуационной оптимизации структуры иерархической системы управления (ИСУ) и многоэтапной оптимизации процесса дооснащения ИСУ. Результаты решения первой задачи являются исходной информацией для решения второй задачи. Вопросы обоснования структуры иерархических систем рассматривались в работе [1] (минимизация количества уровней, оптимизация степени резервирования, расчет характеристик итерационного обмена информацией). Однако алгоритмы координации были разработаны для конкурентной обстановки (задачи Центра и задачи средних и нижних уровней частично не совпадают, в основном из-за необходимости распределения общего ресурса). Рассматриваемые в статье иерархические системы управления созданы и направлены на достижение единой цели, а вопросы координации уже решены на уровне концептуального (внешнего) проектирования, то есть обеспечение решения целевой задачи не требует проведения расчетов по алгоритму Данцига – Вулфа, по алгоритму Корнаи – Липтака и т.п. Следовательно, необходима разработка новой математической модели функционирования ИСУ в условиях вероятностной неопределенности (как при мониторинговом дежурстве, так и в ходе целевого использования). Анализ показал, что процесс информационного обмена в ИСУ адекватно описывается цепями Маркова, однако оперативное перестроение аналитических моделей для условий жестких временных ограничений на ситуационную переработку моделей затруднителен, при этом может иметь место высокая степень эвристичности. Поэтому вместо аналитической необходимо разработать имитационную модель. Процесс создания ИСУ также описывается марковскими моделями [2], что позволяет сформулировать задачу минимизации расхода ресурсов за счет адаптивного реагирования на исход каждого этапа ранних стадий жизненного цикла, при этом должна использоваться частная имитационная модель.
Целью исследования является минимизация расхода средств, дополнительно привлекаемых для ликвидации этапных опозданий при оптимизации процесса модернизации иерархических систем управления, и для ее достижения необходимо решить новую научную задачу по разработке обобщенной и частной имитационных моделей функционирования и развертывания ИСУ.
Применение общей имитационной модели для оценивания результативности подсистем информационного обеспечения. В общем случае результативность ИСУ оценивается вероятностью Pису доведения за заданное время информации, необходимой для каждого отдельного управляемого объекта. Выражения для расчета Pису могут быть получены с помощью теорем сложения и умножения вероятностей для конкретной структурной схемы в соответствии с техническим исполнением (радиолиния, кабельная линия, последовательное смешанное соединение, степень резервирования и т.п.). Исходными данными для расчета Pису являются количественные оценки интенсивности отказов, параметры внешних воздействий, характеристики окружающей среды, параметры структурно-логических схем для каждого уровня ИСУ, технические характеристики конструктивных элементов и вероятности их безотказной работы. В работах [3, 4] показано, что учет возможных сбоев при прохождении информации от верхнего уровня до нижнего (исполнительского и между уровнями наиболее адекватно описывается дискретными цепями Маркова, однако размерность матриц перехода ИСУ из состояния в состояние резко, непропорционально увеличивается при росте числа объектов в каждом звене. Рабочие алгоритмы использования перечисленных аргументов приведены в руководящих документах и справочниках по надежности электронной техники [4, 5]. Кроме того, следует отметить, что при изменении обстановки и, как следствие, при переходе от исходного облика ИСУ к модифицированному (с сохранением количества уровней) необходимо получение (выведение) новой системы выражений для расчета Pису. При этом для каждого нового варианта преобразовании исходного облика ИСУ решение такой аналитической задачи потребует дополнительных временных затрат, что создает риск срыва своевременной подготовки предложений в руководящие документы. Для устранения этого недостатка представляется целесообразным применение метода статистических испытаний. Логика его применения заключается в следующем. Разыгрывается прохождение сигналов на первом уровне. При положительном исходе розыгрыша (удовлетворяются вероятностные условия эквивалентности и выполняются временные ограничения, соответствующие данному уровню) осуществляется переход к следующему уровню ИСУ. При отрицательном исходе данное статистическое испытание считается неудачным, в вычислительном эксперименте организуется новая попытка. При этом предполагается, что для минимизации временной задержки используются ЧЛБ-код и модифицированная криптосистема Мак-Элиса, позволяющая исключить ошибки оператора, контролирующего обратную связь [6].
При имитации временных затрат для иерархических систем, предназначенных для доведения информации до подвижных объектов (ПО), описанная процедура усложняется, так как в сегментах движения модельного времени необходимо учесть возможный уход ПО из зон досягаемости передаваемой информации (географическая недоступность, геофизические факторы, односторонняя блокировка). Закон распределения участков разрыва информационного взаимодействия может быть определен численным методом для конкретных исходных данных (по структуре ИСУ и по обслуживаемым объектам), при этом также проводится дополнительная процедура статистического моделирования.
Для варианта оценивания результативности ИСУ по обобщенному временному показателю tΣ (суммарное (конечное) время доведения требуемой информации) целесообразно предварительное теоретическое обоснование закона распределения величины tΣ с учетом эксплуатационно-технических характеристик конкретного варианта.
Прогнозирование числа обращений D к датчику случайных чисел в ходе имитации прохождения сигналов является самостоятельной задачей, так как нижняя граница возможных значений D равна произведению Ni*Nij*Nijk (Ni – число уровней, Nij – число звеньев в уровне, Nijk – число исполнительных уровней в звене), а верхняя граница является трижды неопределенной случайной величиной. Следовательно, точность расчета Pису. будет определяться шагом заполнения табличного ряда распределения модельного времени.
Применение частной имитационной модели для оптимизации процесса дооснащения ИСУ. Для реализации крупных высокотехнологических проектов характерны определенные отставания хода отработки, особенно на первых этапах [7, 8]. Причины нарушения первоначально объявленных сроков и способы «компенсации» опозданий не являются универсальными. Для рассматриваемых в статье иерархических систем управления основными причинами опозданий являются точечные санкционные воздействия по IT-сфере (диапазон запретов охватывает программное обеспечение, доставку электронно-компонентного оборудования, воздействия на поставщиков и, как следствие, обуславливает временную нехватку специалистов). Компенсация опозданий может быть осуществлена только дополнительными затратами, поэтому возникает актуальная задача поиска вариантов минимизации затрат, зависящих не только от степени нарушения плановых сроков. Анализ работ по управлению инновационными проектами [8] показал, что к настоящему времени в интересах моделирования конкурентной борьбы разработаны различные методики, но все они базируются либо на эконометрическом подходе к составлению и решению систем дифференциальных уравнений, описывающих динамику двусторонних воздействий по потенциальному конкуренту, либо на применении математической теории игр [7]. В современных условиях фрагментации глобальной экономики указанные подходы неприемлемы, так как исходными данными для проведения расчетов по ним являются неизвестные объем, направленность и периоды санкционных воздействий.
Для решения задачи минимизации затрат представляется целесообразным использовать следующий подход. Обозначим:
ТПР – срок, указанный в проекте дооснащения ИСУ;
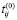– продолжительность работ по установке СПНД для критического пути, рассчитанного при первоначальном формировании плана, то есть
;
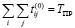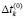– расчетная продолжительность k-го этапа критического пути для первоначально запланированной (исходной) структуры общего плана;
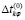– реальное значение этой величины;
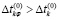, (1)
РПР – требования заказчика в вероятностной форме.
Так как вследствие задержки (1) имеет место неравенство
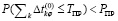, (2)
то возникает риск невыполнения плана дооснащения ИСУ.
Очевидно, на каждом последующем этапе возможно повторение состояния (2). Тогда задача оптимизации процесса дооснащения ИСУ в вербальной постановке заключается в определении вариантов, минимизирующих суммарные дополнительные расходы
.
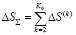Так как исход каждого этапа и, соответственно, величина компенсации опоздания на следующих этапах является случайными величинами, то минимизацию затрат можно проводить только «в режиме реального времени». Вычислительный процесс должен включать два контура – от конца к началу и, далее, от начала по ходу отработки проекта. Реализация ретроспективной развертки позволит сформировать «базу заготовок» (БЗ), включающую комбинации заранее рассчитанных затрат и величин опоздания для каждого этапа и для каждого варианта критического пути общего сетевого плана. Анализ работ по применению сетевых моделей [3, 7] показывает, что изменение продолжительности участков ранее подготовленного общего плана приводит к необходимости поиска нового критического пути для оставшихся после корректировки этапов.
Таким образом, схема алгоритма минимизации затрат не является детерминированной и заключается в «двойном» подборе управляющих воздействий для каждого факта изменения критического пути и для каждого этапа. Реализация такого рода случайной сети наиболее оперативно может быть осуществлена методом статистического моделирования.
Схема соответствующего вычислительного процесса включает следующие действия. После каждого розыгрыша величины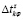 
реализуется алгоритм минимизации (z – номер варианта пересчитываемого критического пути, то есть частотная характеристика действий по реконфигурации общего сетевого плана). Если после очередного статистического испытания устанавливается, что критический путь для оставшихся этапов изменяется, то осуществляется оптимизация новой (сокращенной) последовательности этапов. При этом в БЗ вносятся заготовки новых комбинаций, а динамические параметры выражений, описывающих опоздания и затраты, уточняются на каждом этапе путем организации новой ретроспективной развертки. Далее они вносятся в память комплексов средств автоматизации Центра принятия решений (аппарата руководителя проекта).
После розыгрыша всех этапов формируется расширенная БЗ, включающая рекомендации по выбору наиболее целесообразных действий по перепроектированию в каждой ситуации. Следует отметить, что третью координату массива комбинаций в общем случае нельзя рассматривать как детерминированную, так как перебор комбинаций является эвристическим, т.е. необходимо рассчитывать ее некоторое предельное значение, зависящее от назначенных заказчиком доверительной вероятности и доверительного интервала. Далее подсчитывается статистическая оценка риска невыполнения условия:
,
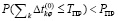которое может использоваться при определении нижней оценки вероятности необходимости привлечения дополнительных средств.
Для расчета математического ожидания минимизируемых затрат на каждом шаге ретроспективной развертки, помимо зависимостей, связующих величину опоздания и величину затрат на компенсацию, необходимо знать закон распределения величины опоздания. Соответствующие зависимости определяются по результатам вычислительных экспериментов; на рисунке предоставлен пример трех вариантов зависимости ΔS(k) от Δt(k). Его анализ показывает, что при опоздании Δt ≤ t1 оптимальным вариантом является вариант устранения опоздания W3, при опоздании t1 ≤ Δt ≤ t2 – вариант W1, при опоздании t3 ≤ Δt ≤ tздр – вариант W2.
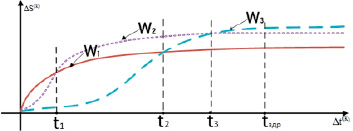
Варианты зависимостей расхода средств на компенсацию опоздания от величины опоздания
Предполагается, что величина tздр определяется заказчиком из соображений здравого смысла; например, возможно, что при величине опоздания более 2/3 от планового значения продолжительности k-го этапа потребуется неприемлемый размер затрат на восстановление плановых сроков по оставшимся этапам.
База заготовок, используемая при оптимизации в ретроспективной развертке и выборе оптимального варианта при «прямых» вычислениях, может содержать не менее десяти вариантов таких зависимостей для каждого шага вычислений. Функция распределения продолжительности каждого (точнее, распределения опоздания) определяется по правилам математической статистики. Как правило, она «существует» только в форме таблиц, содержащих десятки тысяч значений. В отличие от рассмотренных в п. 1 данной статьи интервалов, имеющих порядок единиц минут (для вариантов отсутствия разрывов в информационных воздействиях), рассматриваемые интервалы имеют величину десятков недель или месяцев, поэтому представляется целесообразным аппроксимация функции распределения величины опоздания путем ее пересчета в стандартную функцию нормального распределения. Приведем пример преобразования выборки для гамма-распределения. Обозначим через Fγ(x | p, λ) и, соответственно, через fγ(x | p, λ) функции гамма-распределения и плотности с параметрами р и λ, и пусть Ф(х) – функция стандартного нормального распределения, а φ(х) – его функция плотности. В этом случае приближенно
Fγ(x | p, λ) = Ф(λu),
где λu – переменная, которая по Вильсону – Хилферти [5] имеет вид
,
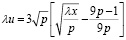а по Фишеру [5] –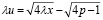 
.
После алгебраических преобразований получаем следующие зависимости:
Первый вариант:
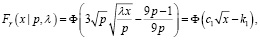
где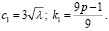 
Второй вариант:
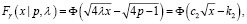
где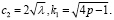 
После интегрирования получаем приближенные функции плотности:
вариант 1 –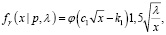 
вариант 2 –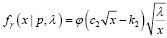 
Следует отметить также, что после выявления новых факторов (по отношению к априорной информации) и их анализа возможно изменение основной гипотезы, «заложенной» в соотношение (3). При этом формат зависимости ΔS(k) от времени для любого планового периода будет определяться логистическими функциями с другими атрибутивными коэффициентами, соответствующими новой производственно-экономической обстановке.
Заключение
В статье предложен подход к решению двух взаимосвязанных задач – ситуационной оптимизации структуры иерархической системы управления и многоэтапной оптимизации процесса дооснащения ИСУ. При решении первой задачи результативность ИСУ оценивается по конечному времени доведения требуемой информации. При оценивании временных затрат для иерархических систем, предназначенных для доведения информации до подвижных объектов, в сегментах имитации модельного времени учитывается возможный уход ПО из зон досягаемости передаваемой информации (географическая недоступность, геофизические факторы, односторонняя блокировка). Закон распределения участков разрыва информационного взаимодействия определяется численным методом для конкретных исходных данных (по структуре ИСУ и по обслуживаемым объектам), при этом проводится дополнительная процедура статистического моделирования. Минимизация расхода средств, дополнительно привлекаемых для ликвидации этапных опозданий, основана на создании и применении в расчетах трехмерного массива комбинаций величин опоздания на контролируемом этапе и расхода средств на ее компенсацию на последующих этапах (горизонт планирования – не более 2 вследствие значительной неопределенности внешней обстановки). Разработанная для сопровождения данного процесса имитационная модель позволяет учитывать возможную реконфигурацию критического пути общего сетевого плана модернизации оптимизационной задачи по исходным данным, соответствующим результатам предыдущих этапов.
Включение предложенных алгоритмов в состав системы математического обеспечения процесса модификации иерархических систем управления позволит обеспечить реализацию планов развертывания ИСУ в кратчайшие сроки. Разработанный методический аппарат целесообразно применять в ходе административно-научного сопровождения хода реализации процесса модификации иерархических систем управления. Точность оценивания прироста эффективности за счет ситуационной оптимизации будет определяться степенью детализации прогнозных моделей воздействий конкурентной среды.
Библиографическая ссылка
Волков В.Ф., Пономарев А.С., Шуваев Н.А. ПРИМЕНЕНИЕ МЕТОДА ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ ПРИ ОПТИМИЗАЦИИ ПРОЦЕССА МОДЕРНИЗАЦИИ ИЕРАРХИЧЕСКИХ СИСТЕМ УПРАВЛЕНИЯ // Современные наукоемкие технологии. – 2024. – № 9. – С. 16-21;URL: https://top-technologies.ru/ru/article/view?id=40142 (дата обращения: 21.11.2024).