Введение
В связи с ростом исследований в области машинного обучения [1, c. 59; 2, c. 33; 3, c. 23] в последние годы передовые технологии открывают новые возможности для робототехнических систем. Методы обработки изображений, основанные на машинном обучении, демонстрируют многообещающий потенциал для решения задач в процессе сборки, например распознавания объектов, определения местоположения и планирования траектории. Необходимы точные и надежные подходы, гарантирующие выполнение решения этих задач.
В актуальных практических задачах робототехнических систем часто приходится определять степень интереса к тому или иному объекту. Поиск объектов невооруженным глазом проще, поскольку люди могут легко обнаружить различные параметры объектов, такие как расположение, цвет, текстура и непрозрачность. Компьютеру требуется значительное время для распознавания и идентификации объектов на изображении. В компьютерном зрении «обнаружение объекта» означает поиск и обнаружение объекта на изображении или видео. Обнаружение объектов включает в себя три основных процесса: извлечение признаков, обработку признаков и классификацию объектов [4, 5]. Обнаружение объектов стало быстрее и точнее благодаря усовершенствованным системам компьютерного зрения. Многие успешные методы «обнаружения объектов» значительно улучшились благодаря внедрению методов машинного обучения.
Целью исследования является разработка математических моделей, численного метода и комплекса программ с использованием теории нечетких множеств для оценки объектов интереса в робототехнических системах с помощью компьютерного зрения. Необходимо получить оценку интереса к объекту не в виде отдельного числа, а в виде функции принадлежности. Например, оценить не только опасность тех или иных наблюдаемых объектов, но и понять, насколько велика уверенность в данном уровне опасности.
Материалы и методы исследования
Как правило, для обнаружения объектов и их идентификации используются технологии компьютерного зрения.
В подобных задачах зачастую велика степень неопределенности. Во многом она обусловлена двумя факторами:
1) неточностью и зашумленностью датчиков робота;
2) неопределенностью нашего отношения к интересу объектов определенного класса.
Первый тип неопределенности связан с техническим несовершенством наших средств изучения реального мира, в идеальном мире он должен стремиться к нулю, но в условиях сложной среды, особенно для наземных роботов, эта проблема не исчезнет еще не одно десятилетие. Второй тип неопределенности связан с фундаментальными склонностями человека к нечетким размытым рассуждениям, в ситуациях противоречивых критериев. Целесообразно учесть эту размытость в системе определения приоритета задач робототехнической системы. Для этого хорошо подходит математический аппарат мягких вычислений [6].
Пусть дан вектор нечетких значений признаков объекта:
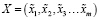, (1)
где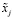 
– значение нечеткого j-го признака характеризуется функцией принадлежности:
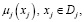(2)
где Dj – домен (множество возможных значений) j-го признака, а μj(xj) – функция принадлежности j-го признака.
Если значение признака нельзя установить – это полная неопределенность:
.
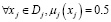Если признак «четкий», то μj(xj) = 1, для некоторого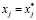 
и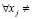 
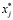μj (xj ) = 0.
Допустимы любые другие μj (xj ) заданные на координатной сетке с высокой степенью точности.
Даны классы объектов интереса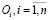 
. И первая задача – это задача нечеткой классификации, то есть определения такого 
.
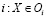Ее решение возможно двумя путями. Первый путь – это построение экспертных правил продукционного типа:
Если некоторое подмножество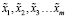 
принимает определенные нечеткие значения, то 
.
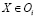Данное правило не дает однозначной принадлежности объекта одному классу. Но лишь распределяет функцию принадлежности объекта на множестве всех номеров классов. В нечетком виде данная импликация выглядит следующим образом:
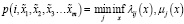, (3)
где λij(x) – принадлежность значения x классу i для переменной j.
Далее возможен переход к «четкой» постановке путем выбора наиболее возможного класса:
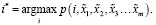(4)
Однако далеко не факт, что не следует обратить внимание на другой объект, хоть и менее возможный, но значительно более интересный.
Если значения признаков перечисляются в продукции через нечеткую дизъюнкцию, то формула (3) примет вид
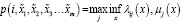. (5)
Данный способ определения нечеткой принадлежности требует задания экспертных суждений в момент проектирования робототехнической системы, что не всегда возможно и требует временных затрат на стройку системы экспертом и инженером по знаниям, кроме того, затруднена полная верификация всех правил нечеткого вывода. Поэтому сейчас часто применяют подход, основанный на машинном обучении. Возможный вариант такого подхода заключается в определении центров классов в пространстве признаков и расчете метрики близости центров классов и конкретных векторов признаков неизвестных объектов. Относительная близость к одному из центров говорит о большей возможности принадлежности соответствующему классу.
Машинное обучение с учителем предполагает наличие обучающей выборки объектов известных классов. Разметка такой выборки – это трудозатратное мероприятие, а использование предобученных моделей машинного обучения содержит определенные риски [7]. Другой способ – это обучение без учителя путем кластеризации объектов. Полученная обученная модель изначально не знает номеров классов, если она правильно выделила их особенности, то требуется сопоставить номера кластеров и классов и далее использовать полученную модель так же, как модель классификации. Сопоставление кластеров классам обычно делает человек, и этот процесс не требует особой квалификации и не занимает много времени.
Рассмотрим подробнее алгоритм метода нечеткой кластеризации:
1. Случайным образом инициализируются k центров кластеров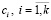 
.
2. Рассчитывается функция принадлежности элементов множества к кластерам по формуле
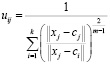, (6)
где uij – функция принадлежности xj к i кластеру; ci – центр i кластера; m – коэффициент нечеткости, 1 < m ≤ ∞, ||∙|| – евклидово расстояние между вектором xj и центром i кластера ci.
3. Переместить центры кластеров исходя из формулы
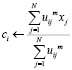. (7)
4. Рассчитать функцию потерь из принципа максимального правдоподобия по формуле
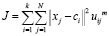. (8)
5. Метод нечеткой кластеризации заключается в итеративной минимизации функции из пункта 4. Если значение функции потерь уменьшается более чем на заданный порог ε, то повторить цикл с пункта 2.
Для рассматриваемого вектора признаков вычисление до найденных центров кластеров выполняются аналогично по формуле (6).
Кроме нечеткой принадлежности классам необходимо определить степень интереса к соответствующим классам. Эта оценка зависит от реальной обстановки, в которой действует робототехнический комплекс, а также от приоритетов, лица, принимающего решения.
В текущей реализации применялась стандартная процедура нечеткого взвешенного суммирования. Она позволяет проводить вычисления в режиме реального времени, в том числе при обработке признаков, полученных из видеопотоков.
Необходимо реализовать численный метод расчета оценки на основе нескольких критериев. Метод должен производить вычисления с нечеткими числами. Интерес к каждому классу объектов будем вычислять по стандартной формуле взвешенной суммы:
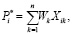(9)
где Xk – нечеткая оценка i-го класса объектов по критерию k, а Wk – нечеткая важность критерия k, не зависит от класса объектов, Pi*– итоговый интерес к объектам класса i.
Правила суммирования и произведения нечетких чисел выполняются на основе принципа общения [8]. Функция принадлежности, соответствующей операции:
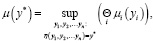(10)
где η – операция, которую требуется применить (в случае вычисления WkXik – это произведение, а для вычисления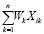 
– это сумма), yi – значения, к которым применяется требуемая операция, μi(yi) – функция принадлежности нечетких значений, μ(y*) – функция принадлежности для результата применения операции η. Θ – это операция пересечения для функций принадлежности [9]. В данной работе – это min, однако существуют и другие разновидности данной операции [10, с. 71]. Обозначим функцию принадлежности полученной нечеткой взвешенной суммы как φi*(y).
Для вычисления итогового интереса наблюдаемого вектора признаков вычисляется клип функция (clip function) по всем возможным классам объектов с учетом их приоритетов и их дальнейшее нечеткое объединение:
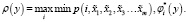(11)
Если получены нечеткие оценки интереса для нескольких объектов, то для них можно описать процедуру нечеткого сравнения. Простейший способ – это дефаззификация:
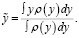(12)
Для того чтобы отразить степень уверенности в выборе объекта интереса, перейдем к парным сравнениям нечетких рангов.
Пусть есть два объекта: Ai и Aj. Тогда нечеткое бинарное отношение между этими двумя объектами: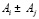 
, то есть объект Ai не хуже, чем объект Aj. Между ними можно установить нечеткое бинарное отношение: 
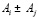. Степень уверенности, что два объекта находятся в отношении 
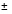задается числом 
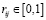. Теперь можно задать матрицу бинарного отношения:
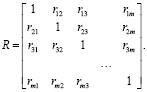(13)
В общем случае данная матрица не может быть ни симметричной, ни обратно симметричной. Элементы данной матрицы можно вычислить с помощью анализа соответствующих объектам Ai и Aj функций принадлежности [9].
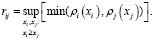(14)
Задавая по данной матрице пороговое знание уверенности θ, можно получить обычное ранжирование объектов:
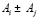, если 
.
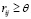Таким образом, разработана математическая модель нечеткой принадлежности по формулам (3)–(5) и нечеткой кластеризации по формулам (6)–(7).
Реализован численный метод нечеткого взвешенного суммирования по формулам (9)–(10).
Разработан комплекс программ на языке Python c использованием библиотек NumPy, Matplotlib, Qt. Комплекс включает в себя:
− оконную программу редактирования классов объектов интереса, их оценок по критериям, задания и визуализации функций принадлежности;
− программу определения центров кластеров;
− консольную программу для интеграции результатов расчетов в робототехническую систему компьютерного зрения.
Результаты исследования и их обсуждение
Общая схема решения задачи следующая:
1. Задаются критерии, по которым оцениваются объекты интереса и их важности (веса). Важности задаются нечеткими числами.
2. Задаются классы объектов интереса. Объект может принадлежать классу объектов. Для каждого класса задаются значения по критериям. Эти значения критериев задаются в форме нечетких чисел.
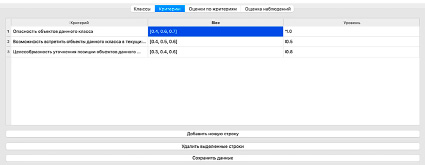
Рис. 1. Редактор весов критериев для веса «Опасность объектов данного класса», равного [0.4, 0.6, 0.7]
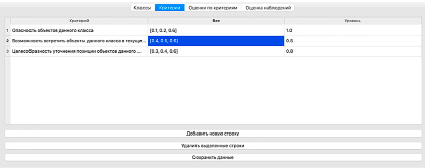
Рис. 2. Редактор весов критериев для веса «Опасность объектов данного класса», равного [0.1, 0.2, 0.6]
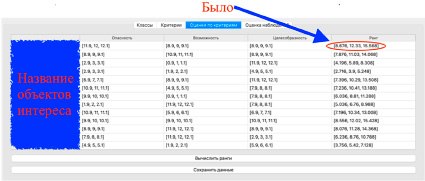
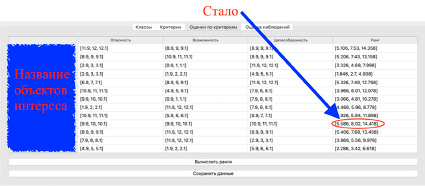
Рис. 3. Список классов объектов
3. Интегральный ранг класса объекта вычисляется на основе значений критериев и их весов.
4. Для наблюдаемого объекта на вход программного обеспечения поступает вектор значений признаков. Так как принадлежность нечеткая, то один наблюдаемый объект может относиться к нескольким классам с разной степенью уверенности.
5. Соотносится интегральная важность каждого класса объектов и степень уверенности что наблюдаемый объект ему принадлежит. В результате вычисляется интегральный интерес (ранг) наблюдаемого объекта.
Далее показано, как при варьировании важности одного критерия изменились интегральные ранги классов и интегральный интерес к одному наблюдаемому объекту.
В рассматриваемом примере интерес к объекту оценивается с помощью трех критериев. Интерфейс ввода и редактирования критериев показан на рис. 1. В первой колонке даны названия критериев. Важности критериев определяются нечеткими весами. Используется треугольная функция принадлежности для нечеткого веса.
На рис. 1 показано, что вес критерия «Опасность объектов данного класса» определяется треугольной функцией принадлежности [0.4, 0.6, 0.7], а на рис. 2 – [0.1, 0.2, 0.6]. Веса остальных критериев в обоих случаях одинаковые.
Суть последующего вычислительного эксперимента – показать, как изменится интегральная оценка наблюдаемого объекта, если поменяются приоритеты критериев.
Веса изменили ранги классов. На рис. 3 показаны оценки объектов интереса. В первой выводятся названия объектов (на рисунке они закрашены синим прямоугольником), далее три колонки, по соответствующим трем критериям из рис. 1 и 2. Последняя колонка – это интегральный ранг объекта, посчитанный по формулам (9) и (10). Ранги нечеткие, поэтому отношения предпочтения между объектами также нечеткие. Верхняя часть рис. 3 соответствует рангам посчитанным весам, показанным на рис. 1, а нижняя часть рисунка соответствует рангам посчитанным весам показанным на рис. 2.
На рис. 4 показано, как используется наблюдение, полученное от системы технического зрения для определения интегрального ранга объекта.
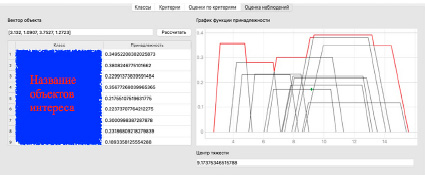
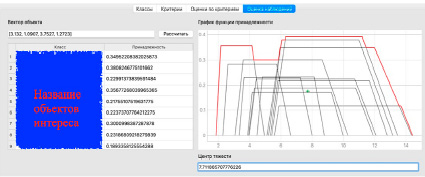
Рис. 4. Оценка вектора признаков
Наблюдаемые значения признаков показаны в левом верхнем углу. На практике – это инвариантные моменты Ху, полученные от системы компьютерного зрения. На основе этих моментов определена нечеткая принадлежность к соответствующим объектам интереса (на рис. 4 их имена закрашены синим прямоугольником). Нижняя и верхняя часть рисунка показывает, как изменяется интегральный интерес к объекту (его ранг) в случае изменения весов. В правой части рисунка показана общая функция принадлежности объекта интереса, посчитанная по формуле (11).
По формуле (11) ранги объединяются в единую функцию принадлежности, и для нее вычисляется центр тяжести по формуле (12), на рис. 4 – это крестик ни графиках справа. Положение креста на оси абсцисс – и есть дефазифицированный интегральный ранг объекта. Видно, что ранг изменяется при изменении веса критерия: был 9.17, а стал 7.71. Таким образом видно, что программа чувствительна к изменению весов критериев.
Заключение
Многокритериальная оценка объектов интереса проводилась с помощью применения моделей и численных методов на основе теории нечетких множеств. В ходе выполнения работы был использован алгоритм нечеткой кластеризации. Было показано, как важность одного критерия может оказать влияние на интегральные ранги классов и интегральный интерес к объекту наблюдения.
Данный метод может быть успешно применен для приоритизации объектов интереса с точки зрения выбора наиболее важных целей. Предложенный подход позволяет учесть, как предпочтения эксперта, так и неопределенности идентификации объектов системой технического зрения.
Библиографическая ссылка
Судаков В.А., Сивакова Т.В. МНОГОКРИТЕРИАЛЬНАЯ ОЦЕНКА ОБЪЕКТОВ ИНТЕРЕСА НА ОСНОВЕ МОДЕЛЕЙ МЯГКИХ ВЫЧИСЛЕНИЙ // Современные наукоемкие технологии. – 2024. – № 8. – С. 81-87;URL: https://top-technologies.ru/ru/article/view?id=40116 (дата обращения: 03.12.2024).