Введение
В работе рассматривали общие нелинейные осцилляторы [1–3]:
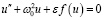, (1)
с начальными условиями
, 
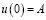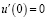, (2)
Здесь f ‒ нелинейная функция от uʺ, uʹ и u. Ограничимся простейшим случаем, когда f зависит только от функции u. Если в задаче Коши, сформулированной уравнениями (1) и (2), отсутствует малый параметр, то в данном случае традиционные методы теории возмущений напрямую применяться не могут. Кроме того, методы возмущений могут привести к потере точности решения из-за необходимости работы с приближенными выражениями. В последнее время большое внимание уделяется анализу нелинейных уравнений без малых параметров.
С целью преодоления описанного выше ограничения разработано множество новых методов. Среди них вариационные методы [4, 5] и метод гомотопического возмущения [6].
Более детальную информацию по упомянутым выше методам можно найти в работах [7, 8]. Также следует отметить работу [9], в которой для линеаризованной системы применен принцип максимума Понтрягина. В методе же энергетического баланса применяется вариационный принцип нелинейных колебаний. В работе [10] показано, что даже аппроксимации низшего порядка обеспечивают высокую точность.
Целью исследования является изучение возможности применения метода энергетического баланса к приближенному решению нелинейных уравнений вибраций и оценке эффективности данного метода по сравнению с методом Рунге – Кутты 4-го порядка.
Материалы и методы исследования
В работе рассматривается общий нелинейный осциллятор вида [4, 5]:
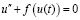, (3)
поскольку u и t ‒ обобщенные безразмерные переменные смещения и времени.
Вариационный принцип легко получить следующим образом:
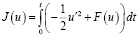, (4)
где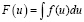 
.
Он является гамильтоновым, поэтому его можно записать в виде
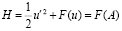. (5)
или
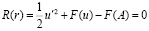. (6)
Колебательные системы содержат два важных физических параметра: частоту ω и амплитуду колебаний A. Рассмотрим начальные условия:
, 
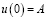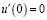. (7)
В первом приближении смещение будем искать в следующем виде:
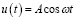. (8)
Подставив уравнение (8) в уравнение (6), получим
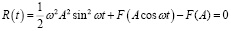. (9)
Если бы случайно в качестве пробной функции было выбрано точное решение, то можно было бы сделать R равным нулю для всех значений t путем соответствующего выбора x. Поскольку (7) является лишь приближением к точному решению, R нельзя везде обнулить. Используя ωt = π/4, получим
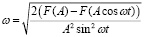, (10)
где T = 2π/ω – период нелинейного осциллятора. Его период можно записать в виде
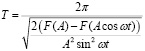. (11)
Результаты исследования и их обсуждение
Для оценки точности метода энергетического баланса, рассмотрим примеры.
Пример 1.
Известно, что свободные колебания автономного консервативного осциллятора с инерционным и статическим типом нелинейностей 5-го порядка описываются уравнением
, 
, 
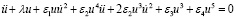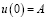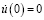. (12)
Предполагается, что движение начинается из положения максимального перемещения с нулевой начальной скоростью; λ ‒ целое число, принимающее значения 1, 0, -1; а ε1; ε2; ε3 и ε4 ‒ положительные параметры, связанные с режимами расчета (таблица).
Значения безразмерных параметров εi в уравнении (12)
|
Режим |
ε1 |
ε2 |
ε3 |
ε4 |
|
1 |
0,326744 |
0,129456 |
0,232555 |
0,087553 |
|
2 |
1,642078 |
0,913067 |
0,313656 |
0,204765 |
|
3 |
4,051875 |
1,665565 |
0,281222 |
0,149667 |
Численное решение (методом Рунге – Кутты 4-го порядка) нелинейного уравнения имеет вид
, 
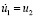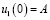, (13)
, 
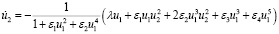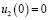. (14)
Решение нелинейного уравнения методом энергетического баланса:
, 
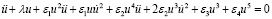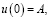
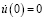. (15)
где u и t ‒ обобщенные безразмерные переменные смещения и времени соответственно. Вариационный принцип описывается следующим уравнением:
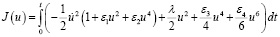. (16)
Поэтому его гамильтониан можно записать в виде
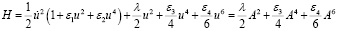(17)
или
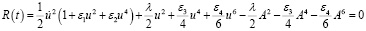. (18)
Колебательные системы содержат два важных физических параметра: частоту ω и амплитуду колебаний A. Итак, рассмотрим такие начальные условия:
, 
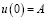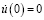. (19)
Первоначальное приближение будем искать в следующем виде:
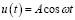. (20)
Подставив уравнение (20) в уравнение (18), в результате получим
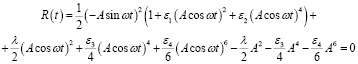. (21)
Что приводит к следующим результатам:
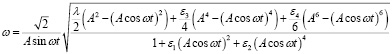. (22)
Кроме того, сравнение этих методологий можно найти на рис. 1.
Если положить ωt = π/4, то в результате получим
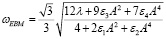. (23)
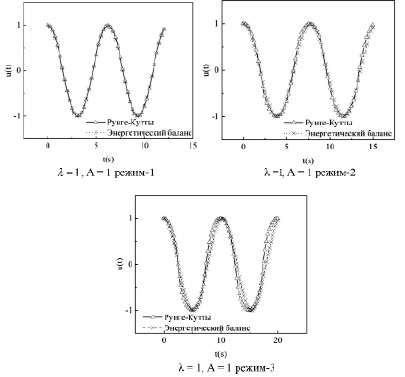
Рис. 1. Сравнение решения метода энергетического баланса и численного решения, решенного методом Рунге – Кутты 4-го порядка, сплошная линия – численное решение и пунктирная линия – решение энергетического баланса.
Подстановка уравнения (23) в уравнение (20) приводит к следующему результату:
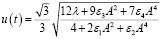. (24)
Предполагается, что движение начинается из положения максимального перемещения с нулевой начальной скоростью.
Пример 2.
Рассмотрим уравнение движения маятника с гармонической точкой стрингера на рис. 2.
Уравнение движения маятника с гармонической точкой стрингера:
, 
, 
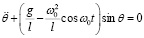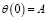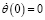. (25)
Это уравнение известно как система с коэффициентами, зависящими от времени.
Численное решение (методом Рунге – Кутты 4-го порядка) маятника с гармонической точкой стрингера:
, 
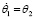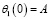, (26)
, 
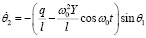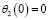. (27)
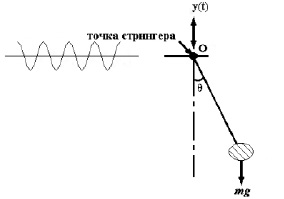
Рис. 2. Маятник с точкой гармонического стрингера: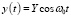 
Решение уравнения маятника с гармонической точкой стрингера по методу энергетического баланса имеет вид
, 
, 
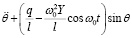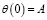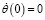. (28)
В котором θ и t ‒ обобщенные безразмерные перемещения и переменные времени соответственно. Его вариационный принцип легко получить как
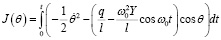. (29)
Поэтому его гамильтониан можно записать в виде
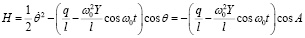(30)
или
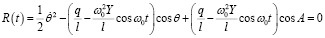. (31)
Рассмотрим начальные условия:
, 
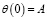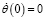. (32)
Предположим, что его первоначальное приближенное предположение можно выразить как
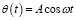. (33)
Подставив уравнение (33) в уравнение (31), получим
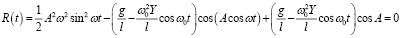(34)
Что приводит к следующему результату:
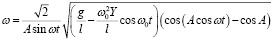. (35)
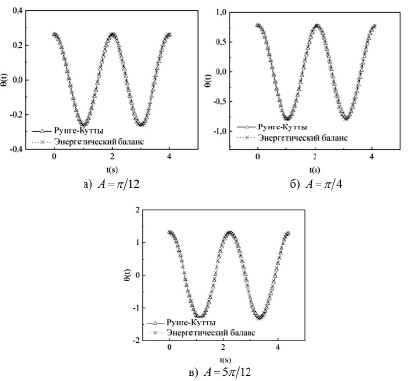
Рис. 3. Сравнение метода энергетического баланса и численного решения, выполненного методом Рунге – Кутты 4-го порядка, сплошная линия – численное решение и пунктирная линия – решение энергетического баланса
Формула (35) при ωt = π/4 перепишется следующим образом:
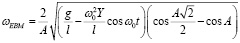. (36)
Подставив уравнение (36) в уравнение (33), получим
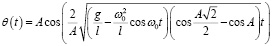. (37)
Для следующих значений параметров было произведено сравнение численного решения с методом энергетического баланса, рис. 3, а–в: L=1 м, ω0 = 1 рад/с, Y = 0,25 м, g = 9,81 м/с2.
Заключение
В данной работе метод энергетического баланса успешно использован для исследования нелинейных уравнений вибрации. Этот метод оказался мощным математическим инструментом для изучения нелинейных уравнений вибрации и может быть легко распространен на любое нелинейное уравнение. На примере решения примеров продемонстрирована точность и эффективность метода. Показано, что полученные решения справедливы для всей области. Примеры показывают, что даже низшие порядки приближений, полученные с помощью настоящей теории, имеют высокую точность 4-го порядка, можно сказать, что оба результата, полученные этими методами, точны и близки друг к другу. Эти примеры иллюстрируют эффективность метода энергетического баланса по сравнению с другими методами.
Библиографическая ссылка
Бадекин М.Ю., Ивахненко Н.Н. ПРИМЕНЕНИЕ МЕТОДА ЭНЕРГЕТИЧЕСКОГО БАЛАНСА К НЕЛИНЕЙНЫМ УРАВНЕНИЯМ ВИБРАЦИИ // Современные наукоемкие технологии. – 2024. – № 8. – С. 28-34;URL: https://top-technologies.ru/ru/article/view?id=40108 (дата обращения: 31.10.2024).