Введение
Исследование рисков эксплуатации объектов энергетики требует построения математических моделей по расчету и прогнозированию уровня безопасности и надежности компонентов оборудования, содержащих трещины. Сам факт наличия и образования трещин в оборудовании в процессе его эксплуатации требует создания систем для их обнаружения. В качестве таких систем широко используются системы неразрушающего контроля, основанные на воздействии сигнала на исследуемую конструкцию, и последующей интерпретации полученного ответа, чтобы определить, найден дефект или нет [1].
Оценка эффективности работы используемых систем контроля имеет вероятностный характер, а для ее определения используются статистические методы. Вероятность обнаружения дефектов зависит как от факторов, присущих самому дефекту (размер и форма дефекта, его ориентация, материал, шероховатость), так и от используемой системы контроля. Чаще всего, в качестве вероятности обнаружения используется зависимость вероятности от размера дефекта, которая получила название кривой достоверности – кривая POD(a) [2].
Целью исследования является разработка методики определения вероятности действительного распределения дефектов и вероятностной кривой обнаружения дефектов (кривой PoD(a)) на основе статистического анализа кривых обнаруженных дефектов, полученных с помощью системы контроля для исследуемых объектов энергетики.
Материалы и методы исследования
Материалами исследования являются результаты распределения обнаруженных дефектов разными системами неразрушающего контроля в контролируемых объектах энергетики.
Методами исследования в данной работе являются статистические методы и реализованные на их основе математические модели и программный код, разработанный на высокоуровневом языке программирования – Python.
Результаты исследования и их обсуждение
Традиционно при решении задачи определения зависимости вероятности обнаружения от размера дефектов (кривая POD(a)) проводят серию специальных лабораторных испытаний с использованием прямых методов. Данные лабораторные испытания проводятся с использованием репрезентативных образцов с уже заранее известными размерами дефектов (трещин) [3].
Прямой метод построения зависимости вероятности обнаружения дефекта (POD(a)) от его размера основан на сравнении результатов числа обнаруженных дефектов, полученных методами неразрушающего контроля металла, с общим числом дефектов, заложенных в образцах. Вероятность обнаружения дефекта размером ai в этом случае определяется по следующей формуле:
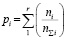, (1)
где ni и nΣi – число обнаруженных и общее число дефектов размера ai; r– число значений pi, соответствующих размеру ai (при объединении данных по нескольким образцам).
Результаты полученных испытаний могут быть представлены в разных формах. Если в результате проверки установлен лишь сам факт обнаружения трещины, то в этом случае данные описываются в терминах – обнаружен дефект или нет. Такие данные называются “да/нет” данными. Примером таких испытаний является визуальный контроль [4].
Для большинства систем контроля регистрация и обнаружение дефектов производится в результате обработки отраженного сигнала. Исследуемый объект облучается исходным сигналом и записывается ответ отраженного сигнала от дефекта. Полученный ответ передается в контролирующее устройство, в котором производится сравнение ответного сигнала с пороговым значением. В этом случае величина отраженного сигнала может быть связана с размером дефекта, что позволяет получить больше информации и построить кривую POD(a) с меньшим числом экспериментов.
В зависимости от формы полученных результатов испытаний могут быть использованы различные статистические модели для количественной оценки надежности систем неразрушающего контроля:
1. Статистическая модель, основанная на биномиальном законе распределения.
2. Параметрическая статистическая модель, предложенная Беренсом и Хови [5], имеющая функциональную форму, зависящую от небольшого числа параметров.
В случае статистической модели, основанной на биномиальном законе распределения, вероятность обнаружения для заданного размера определяется как доля обнаруженных трещин в исходной выборке. Каждый эксперимент рассматривается как последовательность независимых испытаний Бернулли. Для вычисления нижней доверительной границы используется биномиальный закон распределения. Доверительные границы могут быть вычислены лишь для выборки, соответствующей заданному интервалу размера дефектов. Причем эти доверительные границы являются разными для разных интервалов размеров дефекта и поэтому обладают неустойчивым поведением. В этом случае для определения вероятности пропуска дефекта заданного размера надо знать как кривую вероятности обнаружения, так и распределение дефектов по размерам в исследуемой конструкции. К тому же, реализация данной модели является весьма затратной. В работе [6] указано, что для обеспечения доверительной вероятности 95 % для дефектов заданного размера необходимо провести 59 испытаний, то есть иметь для их реализации 59 образцов заданного размера. Такие испытания должны быть проведены для каждого выбранного размера дефекта, то есть если их 59, то общее число испытаний составит 59 на 59.
Альтернативным вариантом биноминальной модели предлагается параметрическая модель для построения PoD кривой. В работах Беренса и Хови [2, 5] применяется иная статистическая основа для представления кривой PoD в виде математической функции. Главная идея статистической модели, которая была предложена Беренсом и Хови [5], заключается в представлении выходного сигнала, поступающего от системы контроля, в виде основной составляющей, связанной с изменениями среднего сигнала от одного дефекта к другому, и случайной составляющей, связанной с изменениями сигнала при проверке того же самого дефекта. Следует отметить, что такие параметры, как местоположение дефекта, свойства самого материала и ориентация дефекта, относятся к первой основной составляющей и не меняются от одного осмотра к другому. Основой второй составляющей являются используемые средства контроля и человеческий фактор. Средства контроля представляют собой сам метод контроля, используемую методику и аппаратуру контроля, а также выбранную чувствительность. Человеческий фактор носит субъективный характер и может изменяться от различных причин. Средства контроля, наоборот, обладают объективными параметрами, и их можно оценить в виде погрешности используемого метода [7, 8].
В соответствии с изложенными представлениями Беренс и Хови [5] предлагают статистическую модель, согласно которой ответный сигнал системы контроля разбит на отдельные компоненты. Эти компоненты могут быть записаны в виде следующей функциональной связи:
â = h(a) + δ + ε, (2)
где â – выходной сигнал, поступающий от системы контроля,
h(a) – основная составляющая, характеризующая среднее изменение сигнала от размера дефекта,
δ – дополнительная составляющая, обусловленная используемыми средствами контроля и определяемая в виде погрешности используемого метода,
ε – дополнительная составляющая, обусловленная человеческим фактором.
Следует заметить, что, согласно Беренсу и Хови, величина h(a) является случайной величиной со своим средним значением, а величины δ и ε – случайные величины с нулевым средним значением.
В работе [5] было отмечено, что наиболее спорным аспектом оценки надежности является выбор модели для функции вероятности обнаружения. В этой же работе авторы исследовали шесть различных форм кривой вероятности обнаружения и пришли к выводу, что лог-логистическая модель наилучшим образом соответствует анализируемым данным (данные были взяты из программы «Have Cracks, Will Travel» ВВС США [9]). Лог-логистическая, используемая для данных “да/нет”, записывается следующим образом:
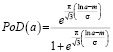, (3)
где a – размер дефекта; m – логарифм размера, на котором PoD = 0,5; σ – величина, обратная наклону прямой регрессии. Явным преимуществом, которое она предлагает, является ее особенно прямая аналитическая управляемость в сочетании с гораздо более эффективным использованием информации, содержащейся в двоичных данных попаданий/промахов.
Обозначив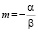 
и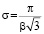 
получим
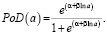(4)
Здесь PoD(a) – средняя функция вероятности обнаружения для каждого дефекта размером a, α и β – параметры кривой.
Параметры α и β можно получить методом линейной регрессии из соотношения описывающего линейную зависимость натурального логарифма коэффициента разногласия odds от натурального логарифма размера дефекта a:
ln(odds) = α + β lna, (5)
где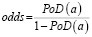 
.
Подставляя полученные значения α и β в формулу (4), получаем зависимость PoD(a) для исходной выборки.
Для нахождения нижней доверительной границы зависимости PoD(a) вычисляют нижний доверительный интервал линейной регрессии по следующей формуле:
α ± tϑ,n–2 ∙ SEy, (6)
где SEy – стандартная ошибка регрессии, tϑ,n–2 – квантиль распределения Стьюдента с уровнем значимости ϑ и n – 2 числом измеренных точек.
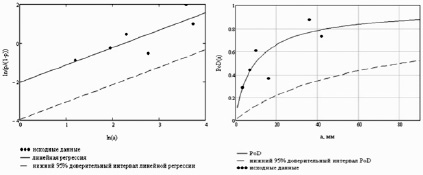
Рис. 1. Построение лог-логистической кривой в координатах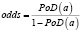 
, lna (слева), в координатах PoD(a), а (справа)
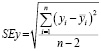, (7)
где yi – истинное значение в i-й точке; yi – значение в i-й точке, предсказываемое линейной регрессией; n– число точек, по которым строится регрессия.
Примеры полученной нижней доверительной границы зависимости PoD(a) изображены пунктирной линией на рис. 1.
Используя полученные кривые PoD(a) и имея обработанные массивы обнаруженных дефектов для исследуемой области, содержащих трещины, могут быть получены распределения действительных дефектов, которые и используются в дальнейшем для прогнозирования уровня безопасности.
Следует заметить, что условия проведения лабораторных исследований, для нахождения кривой достоверности POD(a) и проведение контроля в период эксплуатации объекта существенно отличаются. Кроме всего прочего это связано и с разным уровнем квалификации рабочих групп, проводящих контроль. Существенная разница при нахождении дефектов разными группами была отмечена при проведении межлабораторных сравнительных испытаний в период с 2018 по 2019 г. в организациях атомной отрасли по неразрушающим видам контроля. В МСИ приняли участие 16 организаций, входящих в контуры управления АО «Атомэнергомаш», Концерна «Росэнергоатом» и ядерного оружейного комплекса Государственная корпорация по атомной энергии «Росатом» [10].
По результатам проведенного разными лабораториями анализа был отмечен большой разброс в данных контроля. Результаты двух из тринадцати лабораторий, которые не обнаружили дефектов длиной 44 мм, оказались неожиданными. Также сильно различались результаты контроля для дефекта длиной 16 мм (пять из тринадцати лабораторий этот дефект не обнаружили). По причине малого числа данных, полученных отдельными лабораториями для дефектов одного размера, невозможно было построить кривые PoD(a) для отдельных лабораторий. Поэтому были приведены результаты лишь для усредненных кривых PoD(a), полученных в результате проверок разными лабораториями. Следует заметить, что данная ситуация является типичной при построении кривых PoD(a).
В период подготовки к сдаче в эксплуатацию (при проведении входного и предэксплуатационного контроля) и в период эксплуатации объектов (эксплуатационный контроль) накапливается большой объем экспериментального материала по исходной дефектности в виде исходных выборок, обнаруженных с помощью различных систем контроля и различными бригадами [11, 12]. Использование полученного материала для анализа влияния образования дефектов рассматриваемого объекта исследований от разных факторов с целью оптимизации условий эксплуатации – затруднительно. Поскольку полученные данные в виде обнаруженных дефектов «смешаны» как с данными по действительному распределению дефектов, так и с данными, используемыми разными системами контроля, а также рабочими группами, которые проводят контроль. В этом случае становится весьма актуальной задача по выделению из исходной выборки как обнаруженных дефектов – функции вероятности обнаружения PoD(a), так и действительного распределения плотности дефектов – pa(a). Предложенный в работах [2, 5] расчетный метод, основанный на решении обратных задач, дает возможность решить эту задачу. В этом случае полученные данные могут быть предварительно классифицированы по различным признакам, и для каждой отдельной выборки найдена кривая PoD(a), а также действительное распределение плотности дефектов – pa(a) [13].
Следует заметить, что накапливаемая информация по дефектности в период эксплуатации различных объектов является ценным источником для проведения полноценного анализа и построения различных функциональных зависимостей дефектности от параметров эксплуатации. При наличии таких зависимостей могут быть построены математические модели эксплуатации исследуемых объектов и выбраны оптимальные режимы их эксплуатации.
Для аналитического описания кривой PoD(a) в рассматриваемом методе используется экспоненциальная зависимость вида [14]
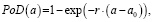(8)
где r – коэффициент достоверности исходной системы контроля;
a0 – чувствительность исходной системы контроля (представляет собой минимальный размер дефекта, который может быть успешно детектирован исходной системой), а для действительного распределения плотности дефектов по размерам экспоненциальная зависимость в виде
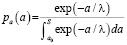, (9)
где λ – параметр действительного распределения дефектов,
S – характерный размер исследуемой области, например толщина стенки трубы.
У коэффициента достоверности, приведенного в формуле (8), параметр r включает как основную составляющую изменения функции PoD(a) от размера дефекта, так и дополнительную составляющую, обусловленную условиями эксплуатации исследуемого объекта, а также человеческим фактором.
Пусть для находящегося в эксплуатации в течение времени t изучаемого объекта были детектированы дефекты различных размеров ai. Формируя для полученной выборки частотную характеристику дефектов по размерам, можно сопоставить ей плотность распределения обнаруженных дефектов – pf (a). В качестве размера дефекта ai должен быть выбран размерный масштаб – длина и глубина, а также площадь сечения дефекта. По причине несовершенства используемой системы контроля определенная часть дефектов оказывается необнаруженной. Степень несовершенства системы измерения характеризуется кривой обнаружения PoDSC(a), где нижний индекс SC относится к конкретной системе контроля. Совокупность обнаруженных и необнаруженных дефектов образует действительное случайное распределение дефектов по их размерам – pa(a).
Используя предложенную в работах [2, 5] статистическую модель, сформируем смоделированные данные на основе известной генеральной совокупности в виде исходной выборки обнаруженных дефектов. Задавая исходные параметры для плотности вероятности действительного распределения дефектов – pa(a), а также для кривой обнаружения дефектов – PoDSC(a), запишем выражение для плотности распределения обнаруженных дефектов в следующем виде:
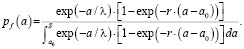(10)
Используя формулу (10), сформируем модель исходной выборки обнаруженных дефектов для заданных исходных параметров: a0, λ, r, NΣ.
Приведем следующий пример расчета, показывающий получение кривой PoDSC(a) и действительного распределения дефектов, по известной характеристике обнаруженных дефектов pf(a) на основе заданных исходных параметров генеральной совокупности.
Несомненным преимуществом смоделированных таким образом данных является то, что можно сравнить полученные результаты с истинным поведением.
Зададим следующие исходные данные:
− число действительных дефектов
Nsum = 100;
− параметр действительного распределения дефектов – λ = 2[мм];
− коэффициент достоверности исходной системы контроля – r = 0,5[1/мм];
− коэффициент чувствительности исходной системы контроля – a0 = 0,5 [мм];
− толщина стенки трубы – S = 20 [мм].
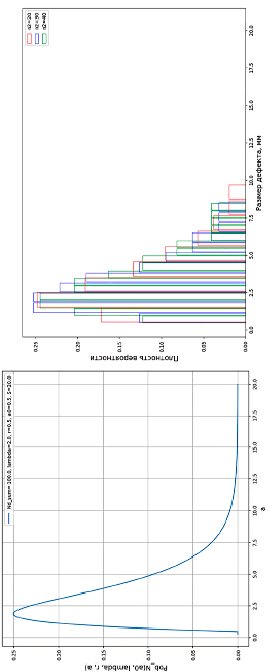
Рис. 2. Функция распределения вероятности (слева) и выборка обнаруженных дефектов (справа)
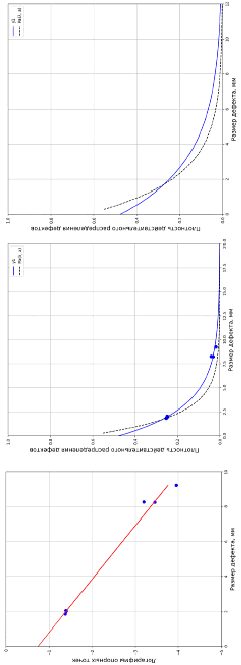
Рис. 3. Полученные зависимости плотности распределения действительных дефектов в логарифмических координатах (слева), в обычных координатах (по центру), сопоставление восстановленного значения плотности распределения действительных дефектов (справа)
Координаты точек
|
Число разбиений исходной области, n |
Координаты экстремальной точки, мм |
Координаты правых конечных значений, мм |
Коррекция правых конечных значений для y, мм |
||
|
a_ext |
y_ext |
a |
y |
y |
|
|
20 |
2,039 |
0,248 |
9,224 |
0,019 |
0,0095 |
|
30 |
1,845 |
0,253 |
8,233 |
0,032 |
0,016 |
|
40 |
2 |
0,245 |
8,25 |
0,041 |
0,0205 |
Используя формулу (10), получим функцию распределения вероятности обнаруженных дефектов по размерам, график которой приведен на рис. 2 (слева).
Если разбить исходный размер S на 20 одинаковых интервалов и вычислить количество действительных дефектов, попавших в эти интервалы, то полученные значения числа действительных дефектов составят: (40, 24, 14, 9, 5, 3, 2, 1, 1).
Из этих действительных дефектов будет обнаружена лишь часть дефектов, которая определяется используемой системой контроля. В данном случае эта система имеет следующие характеристики: (a0 = 0,5[мм]; r = 0,5[1/мм]). Для данной системы число обнаруженных дефектов по размерам составит: (9, 13, 10, 7, 5, 3, 2, 1,1).
Полученное число обнаруженных дефектов по размерам составит исходную выборку дефектов по размерам в рассматриваемой модели. По ней надо восстановить число действительных дефектов по размерам, соответствующее исходной выборке, а также получить кривую достоверности вероятности обнаружения дефектов – PoDSC(a).
Приведенные данные в исходном примере определяют детерминированные параметры распределений исходной генеральной совокупности. Полученная исходная выборка числа обнаруженных дефектов является случайной. График, где отражена зависимость распределения плотности обнаруженных дефектов по размеру приведен на рис. 2 (справа).
Согласно отраженной в работе Беренса методике координаты экстремальной точки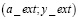 
распределения плотности обнаруженных дефектов совпадают с координатами плотности распределения действительных дефектов [2]. Важно отметить, что полученные координаты экстремальной точки также являются случайными.
Разобьем исходный размер S дополнительно на 30 и 40 интервалов и определим зависимость распределения плотности обнаруженных дефектов. Графики распределения плотности обнаруженных дефектов для этих вариантов приведены также на рис. 2 (синий и зеленый).
Кроме экстремальной точки распределения обнаруженных дефектов, можно использовать правые конечные точки полученных распределений, которые также совпадают с экспоненциальным распределением действительных дефектов. Полученные значения координат этих точек приведены в таблице.
Используя приведенные в таблице значения, с помощью метода линейной регрессии была получена нормированная плотность распределения действительных дефектов pa(a).
Результаты расчетов приведены в виде зависимости плотности распределения действительных дефектов по размерам на рис. 3 (слева и в центре), сопоставление восстановленного значения плотности распределения действительных дефектов (lambdaexp) с исходным значением генеральной совокупности (lambda) также приведено на рис. 3 (справа).
Используя полученное значение для параметра lambdaexp и подставляя его в формулу (10) для обнаруженных дефектов, а также подбирая значение параметра r1 таким образом, чтобы разность квадратов между полученным значением для обнаруженного распределения и исходного распределения для выборки была минимальна, получим
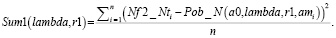(11)
График зависимости функции (11) от параметра r1 представлен на рис. 4 (слева), полученные значения для lambdaexp и r1 дают возможность восстановить распределение обнаруженных дефектов по исходной выборке. Сопоставление этих распределений также наглядно приведено на рис. 4 (справа).
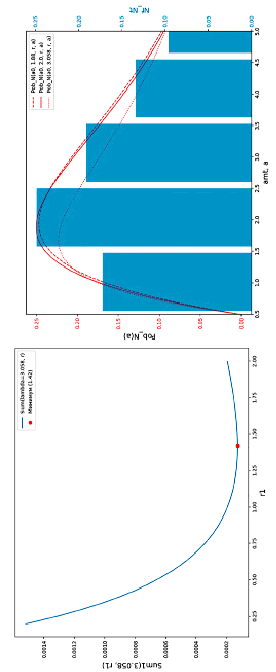
Рис. 4. График зависимости функции (11) от r1 (слева) и сопоставление распределений (справа)
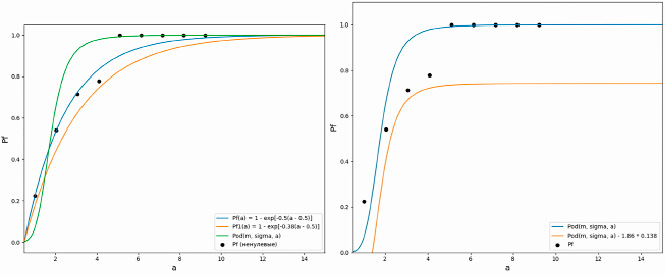
Рис. 5. Графики логистической и экспоненциальной кривых (слева) и реперные значения вероятностей обнаружения дефектов для исходной выборки (справа)
Используя полученные значения lambdaexp и r1, вычислим суммарное число действительных дефектов по следующей формуле:
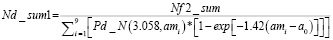. (12)
Зная полученное значение Nd_sum1, были определены распределения действительных дефектов по размерам:
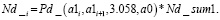(13)
По формуле
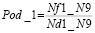(14)
были вычислены реперные значения вероятностей обнаружения для исходной выборки.
С использованием приведенных ранее формул (2)–(10) были построены графики для логистической и экспоненциальной кривой PoDSC(a) по заданной исходной выборке обнаруженных дефектов, приведенные на рис. 5 (слева). Также на рис. 5 отражены реперные значения вероятностей обнаружения дефектов для исходной выборки (справа).
Заключение
На основе статистической модели, приведенной в работе А.Е. Александрова об оценке достоверности результатов контроля металла, была разработана методика восстановления кривой вероятности обнаружения дефектов PoDSC(a) и вероятности распределения действительных дефектов pa(a), а также вычислено суммарное число действительных дефектов Nsum по исходной выборке обнаруженных дефектов.
На основе разработанной методики приведен пример расчета параметров λ, r, NΣ для заданных исходных данных:
− число действительных дефектов
Nsum = 100;
− параметр действительного распределения дефектов – λ = 2 [мм];
− коэффициент достоверности исходной системы контроля – r = 0,5 [1/мм];
− коэффициент чувствительности исходной системы контроля – a0 = 0,5 [мм];
− толщина стенки трубы – S = 20 [мм].
Результаты восстановления параметров λ, r, NΣ решения обратной задачи сравнивались с исходными параметрами. Погрешности расчетов составили: для λ = 14 %; для r1 = 43 %; и Nsum = 17%.
Используя полученные значения для lambdaexp и Nsum, были вычислены реперные значения вероятности обнаружения дефектов для исходной выборки.
Полученные реперные точки могут быть использованы для построения различных функциональных форм кривых PoDSC(a). В работе приведены графики логистической и экспоненциальной кривых вероятностей обнаружения дефектов, а также представлен график логистической формы кривой PoDSC(a) и нижний доверительный интервал, полученный для исходной выборки.
Библиографическая ссылка
Александров А.Е., Клешнин Н.Г. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КРИВЫХ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ ОБНАРУЖЕНИЯ ДЕФЕКТОВ ОБЪЕКТОВ ЭНЕРГЕТИКИ // Современные наукоемкие технологии. – 2024. – № 8. – С. 10-21;URL: https://top-technologies.ru/ru/article/view?id=40106 (дата обращения: 23.11.2024).