Введение
Вероятностные и статистические методы становятся всё более востребованными в научных исследованиях, инженерных и экономических расчетах. В то же время многие инструменты и средства вероятностно-статистического анализа носят эвристический характер. Соответственно возрастает роль качественной подготовки специалистов различных областей по теории вероятностей и математической статистике. В противном случае как отсутствие глубокого понимания сути используемых методов, так и недостаток практики могут привести к неточным результатам и ошибочным выводам. Проблема освоения студентами вероятностных разделов математики справедливо беспокоит исследователей сферы образования [1, 2]. Авторы приложили немало усилий для обоснования необходимости формирования вероятностного подхода к научному познанию студентов, считая этот подход элементом профессиональной культуры специалиста [3].
Среди проблематики применения вероятностно-статистических методов большое место занимают вопросы точности и надежности статистических оценок [4, 5]. С ними тесно связаны поиски оптимального размера выборки [6]. Неадекватный размер выборки, полученный, например, вследствие произвольного толкования уровня надёжности, может послужить источником ошибочных выводов [7]. В настоящее время выявлены многочисленные факты недопонимания терминологии и сущности интервального оценивания как исследователями в области психологии, медицины, биологии [8], так и педагогами и учащимися [9]. Более того, подвергается сомнению сама идея существующего метода интервального оценивания. Дело в том, что произвольная трактовка понятий «доверительный интервал (confidence interval)», «точность/ошибка (margin of error)», «доверительная вероятность/надёжность (confidence probability/reliability)» может привести к манипуляции данными с целью получить обоснование выдвигаемой гипотезы [10]. Предлагаются альтернативные способы построения доверительных интервалов, оценки и интерпретации их параметров [11, 12]. Таким образом, актуальной является задача формирования адекватных представлений студентов о связи точности и надёжности при оценке вероятности.
Настоящая работа продолжает исследования авторов в области разработки средств формирования у студентов вузов вероятностного подхода к научному познанию. Этому аспекту преподавания теории вероятности и математической статистики обычно не уделяется достаточного внимания, несмотря на то, что роль стохастических методов в инженерной и экономической практике постоянно возрастает.
В статье [13] были исследованы границы применимости приближенной формулы Пуассона, а также интегральной теоремы Лапласа, заменяющих точную формулу Бернулли при повторных испытаниях. Варьируемым параметром является число испытаний. При этом авторы большинства учебных материалов рассматривают случай симметричного распределения Бернулли при р = 0,5. Разумеется, в этом случае сходство с колоколообразной гауссовой кривой нормального распределения достигается при относительно небольшом числе испытаний n. В цитируемой статье рассматривается несимметричное распределение с р = 0,25. Авторы, в частности, показали, что уже при n = 20 несимметричный полигон распределения достаточно хорошо аппроксимируется симметричным гауссовым аналогом. Полученные графики используются авторами при чтении лекций, способствуя формированию у студентов 2 курса вероятностного подхода к научному познанию.
В работе [14] исследования точности приближенных вероятностных моделей были продолжены. Фокус исследования направлен на изучение зависимости от вероятности р величин абсолютной и относительной ошибки приближённой формулы Пуассона по сравнению с точной формулой Бернулли. Полученные графики дают возможность выбирать ту или иную вероятностную модель на основании допустимой величины ошибки.
Основное содержание работы [15] заключено в сопоставлении моделей выбора из конечных и условно бесконечных банков элементов. Показано, что приемлемая точность достигается уже при выборе из банка объёмом 100 элементов. Например, вероятно, столько случаев необходимо рассмотреть, чтобы дать обоснование принципа Парето «20 на 80»: 20% усилий дают 80% результата.
По сути, эти выводы не являются отвлечёнными, а имеют большое практическое значение, например, в теории надёжности. Они связаны со статистическим определением вероятности. Наиболее важный случай – определение вероятности практически невозможного события, которая зависит от опасности для жизни, здоровья людей, размера экологического ущерба и т.д., которые может вызвать реализация практически невозможного события. Например, вероятность аварии на атомной станции полагается приблизительно
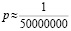 .
.
Ясно, что история ядерной энергетики слишком коротка для того, чтобы накопить опыт такого рода аварий для назначения практически невозможного события с такой вероятностью. Поэтому здесь величина р определяется эвристически, или экспертно. Вероятность же выхода из строя электрической или иной сети, успеха или неуспеха инвестиции, предполагаемого роста объёма продаж и т.п. вполне может быть смоделирована на конечном числе опытов, хотя, выражаясь в процентах, демонстрирует как бы выбор из бесконечного банка вариантов.
Цель настоящего исследования – во-первых, получить простые и наглядные инструменты (графики, формулы), которые в максимально доступной форме демонстрировали бы студентам связь точности и надёжности оценки вероятности при различных значениях самой вероятности и объёма выборки; во-вторых, подобрать относительно простые аппроксимации для зависимостей точности оценки вероятности от её надежности; в-третьих, исследовать погрешность найденной аппроксимации для разных значений объёма выборки.
Материалы и методы исследования
Для определения точности и надёжности оценки вероятности при больших объёмах выборки обычно предполагается близкий к нормальному закон распределения случайной величины. Это делает возможным применение формулы Муавра-Лапласа:
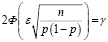 ,
,
где р – оценка вероятности, Ф – интегральная функция Лапласа, ε – точность (ошибка) оценки вероятности, γ – надёжность оценки вероятности (доверительная вероятность), n – объём (размер) выборки. Приведённые в скобках названия являются переводами терминов, наиболее частотных в англоязычных источниках. В настоящем исследовании преимущественно будут использоваться термины «ошибка» и «надёжность», которые лучше отражают специфику анализа проблемы.
Ввиду имплицитного характера формулы Муавра-Лапласа относительно ε и n, а также недостатка времени, отведенного для изучения вероятностных разделов математики, студенты обычно слабо представляют характер связи между надёжностью оценки вероятности и её ошибкой (точностью). Это означает недостаточность сформированности компетенции в области интервального оценивания, которая может привести либо к неправильным выводам относительно надёжности практических расчётов, либо к сознательному или неосознанному навязыванию ошибочных представлений клиентам, заказчикам и т.п. В худшем случае ошибка оценки и её надёжность рассматриваются как независимые параметры при фиксированном объёме выборки.
В настоящем исследовании проблематика точности вероятностных моделей исследуется с точки зрения обеспечения требуемой точности оценки вероятности. Основным методом исследования является вычислительный эксперимент.
Результаты исследования и их обсуждение
Приведённая выше формула Муавра-Лапласа связывает три параметра выборки: ошибку оценки ε, надёжность оценки γ и объём выборки n. Варьируемым в дидактических целях параметром является величина оценки вероятности р. В так называемых прямых задачах исследуется зависимость надёжности от заданной точности оценки. При этом надёжность
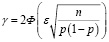
выражается эксплицитно. Практически во всех учебных пособиях для вузов приводятся графики интегральной функции Лапласа Ф, поэтому для студентов не будет затруднительным представить характер изменения надёжности при варьируемой точности оценки. Возможно, в целях обеспечения наглядности при формировании вероятностного подхода преподавателям следует привести семейство подобных зависимостей γ от ε при изменении n и/или р в качестве параметров.
В случае же решения так называемых обратных задач исследуется зависимость ε от γ, или n от ε и γ. При этом
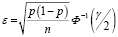 ,
,
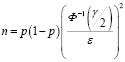 .
.
Поведение обратной функции Лапласа хорошо представляют себе студенты физико-математических направлений подготовки. Студенты же технических, экономических и, особенно, гуманитарных направлений обычны не обладают достаточными компетенциями в области теории обратных функций. Этот раздел математики в настоящее время обычно преподаётся в конспективном стиле, без выполнения практических, тем более контрольных заданий. Авторы не раз сталкивались, например, с неправильными представлениями о взаимосвязи характеристик возрастания-убывания прямой и обратной функции. Это значит, что для формирования компетенций студентов в области интервального оценивания вероятности необходимо иметь средства, обеспечивающие доступность и наглядность информации. Тем более это справедливо для оценивания объёма выборки ввиду возможности варьирования двух параметров ε и γ одновременно. Такими средствами обычно служат графики, которые можно построить, не обращаясь к теории отображений.
Были проведены следующие вычислительные эксперименты:
1. Для четырёх значений n = 20; 100; 500; 1000 и пятнадцати значений р = 0,0001; 0,0005; 0,001; 0,005; 0,01; 0,05; 0,10; 0,15; 0,20; 0,25; 0,30; 0,35; 0,40; 0,45; 0,50 проведены расчеты зависимости ошибки ε от надёжности γ в диапазоне значений надёжности от 75% до 100%.
2. Построены графики найденных эмпирических зависимостей.
3. Подобраны аппроксимации найденных эмпирических зависимостей с помощью полиномиальных и иррациональных функций.
Ясно, что в силу симметрии формулы Муавра-Лапласа по р относительно 0,5, нет необходимости проводить вычислительные эксперименты для значений р > 0,5, и детализировать их для значений р, близких к 1.
Для наглядности приведены два графика из серии вычислительных экспериментов, обозначенных в п.1 (рис. 1, 2).
Анализ приведённых графиков показал, что с ростом объёма выборки величина ошибки существенно снижается. Так, при надёжности γ = 75% ошибка ε будет минимальной для рассматриваемых областей вариации параметров при р = 0,05. Так, для n = 20 получается εmin = 5,61%, в то время как для n = 1000 оказывается εmin = 0,79%. Это означает, что доверительный интервал для оцени 5%-ной вероятности составляет:
(5% – 5,61%; 5% + 5,61%) =
= (-0,61%; 10,61%) для n = 20, и
(5% – 0,79%; 5% + 0,79%) =
= (4,21%; 5,79%) для n = 1000.
Ясно, что для n = 20 такая оценка вообще лишена смысла, поскольку величина ошибки превосходит само оцениваемое значение вероятности. Этот факт иллюстрирует положение о важности оценки минимального объёма выборки.
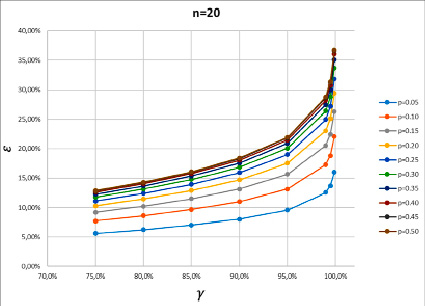
Рис. 1. Зависимость точности оценки вероятности ε от надёжности оценки γ для объема выборки n = 20 при десяти различных значениях оценки вероятности р от 0,05 до 0,50
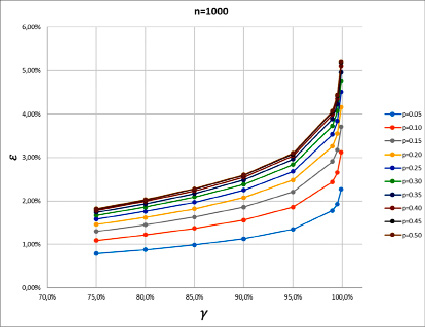
Рис. 2. Зависимость точности оценки вероятности ε от надёжности оценки γ для объема выборки n = 1000 при десяти различных значениях оценки вероятности р от 0,05 до 0,50
Необходимо акцентировать внимание студентов на недопустимости таких «оценок» в практических расчётах. С ростом n от 20 до 1000 доверительный интервал уменьшился в 6,7 раза, что говорит о достаточно высокой точности исследования при, однако, не слишком большом 75%-ном значении надёжности оценки.
Если взять приемлемые значения надёжности, например γ = 95%, то ошибка при р = 0,05 для n = 20 получается ε0,95 = 9,55%, в то время как для n = 1000 оказывается ε0,95 = 1,35%. Это означает, что доверительный интервал для оцени 5%-й вероятности составляет:
(5% – 9,55%; 5% + 9,55%) =
= (-4,55%; 15,55%) для n = 20, и
(5% – 1,35%; 5% + 1,35%) =
= (3,65%; 6,35%) для n = 1000.
Ясно, что, как и в случае минимальной ошибки, оценка 5%-ной вероятности для n = 20 не должна приниматься в расчёт. С ростом n от 20 до 1000 доверительный интервал уменьшился в 7,4 раза. Его половина составляет 27% от самой оценки, что, разумеется не свидетельствует в пользу высокой точности оценки, но в некоторых случаях грубой прикидки такой выбор параметров может быть приемлемым.
Также характер зависимости ε от γ для всех графиков в целом представляется одинаковым: относительно пологий, практически линейный участок до значения γ = 90% (или 95%) сменяется участком быстрого нелинейного роста. Особенно наглядно это выразилось при построении графиков для одного и того же значения оценки вероятности в одних осях для разных объёмов выборки n. На рис. 3 для примера выбрано р = 0,05.
Это означает, что выбирать величины надёжности, большие 95% следует с осторожностью, поскольку это сопровождается резким ростом ошибки оценки. Например, при объёме выборки n = 500 в пограничной точке γ = 95% значение ошибки оценки составляет ε0,95 = 4,38%, что в некоторых случаях может ещё рассматриваться в качестве приемлемой точности вычислений.
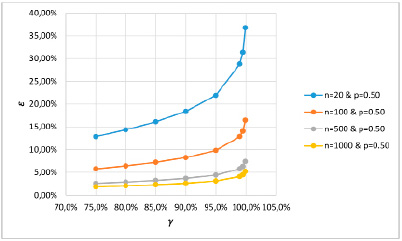
Рис. 3. Зависимость точности оценки вероятности ε от надёжности оценки γ для р = 0,5 и при различных объемах выборки n в диапазоне от 20 до 1000
Это же значение при объёме выборки n = 100 составляет уже ε0,95 = 9,8%, что вызывает сомнение в качестве исследования. Действительно, доверительный интервал 50%-ной оценки вероятности составляет:
(50% – 9,8%; 50% + 9,8%) =
= (40,2%; 59,8%) для n = 100.
Это означает, например, что рейтинг некоей компании может колебаться в широком диапазоне практически от 40% до 60% с надёжность оценки в 95%. Представляется, что малая информативность такого опроса с такой оценкой не вызывает сомнений, несмотря на высокую степень его надёжности. Можно предполагать, что гипотетически точные оценки, приводимые в средствах массовой информации, имеют низкий уровень надёжности.
Наконец, для быстрой оценки величины точности ε в зависимости от величины надёжности γ были предложены аппроксимации, включающие только степенные (целые и дробные) функции. Были предложены две модели аппроксимации.
Модель 1 предполагает использование единой приближённой формулы для аппроксимации зависимости ε(γ):
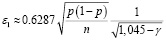 .
.
Модель 2 предполагает использование различных формул для аппроксимации зависимости ε(γ) на двух смежных интервалах изменения надёжности γ:
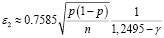
при 75% ≤ γ ≤ 90%,
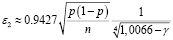
при γ > 90%.
Для анализа точности моделей были найдены абсолютные погрешности оценки точности моделей 1 и 2 по сравнению с табличными значениями обратной интегральной функции Лапласа εтабл:
Δ1 = |ε1 – εтабл|; Δ2 = |ε2 – εтабл|.
Была исследована зависимость абсолютных погрешностей вычислений значения ошибок оценки вероятности Δ1 и Δ2 от величины самой оценки р. Объём выборки принят n = 500. Графики этих зависимостей приведены на рис. 4.
Следует пояснить, что на рис. 4 на логарифмической шкале по оси абсцисс отложены условные единицы, соответствующие
1 → p = 0,00001; 2 → p = 0,0001;
3 → p = 0,001; 4 → p = 0,01; 5 → p = 0,1.
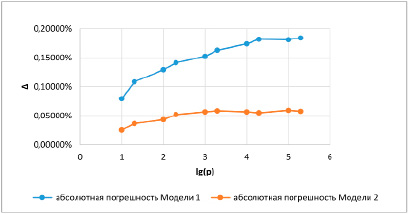
Рис. 4. Зависимость абсолютных погрешностей Δ1 и Δ2 вычисления ошибки ε оценки вероятности р двух приближённых моделей по сравнению с табличными значениями
Анализ графиков, приведенных на рисунке 4, показал, что самое большое по модулю значение абсолютной ошибки при р = 0,5 не превышает 0,2%, что свидетельствует о высокой точности аппроксимации обеих моделей. Близкий к монотонному характер поведения функций абсолютной ошибки, отсутствие пересечения графиков демонстрирует превосходство модели 2 над моделью 1 по точности аппроксимации. Это значит, что обе модели могут быть внедрены в методическое обеспечение университетского курса теории вероятностей и математической статистики для поддержки освоения студентами методов интервального оценивания. Причем графики, подобные приведённым на рис. 1 – рис. 3, могут быть рекомендованы для демонстрации подходов, связанных с интервальным оцениванием долей и вероятностей, даже для студентов физико-математических направлений подготовки.
Заключение
Проведенные вычислительные эксперименты позволили авторам, во-первых, получить визуализацию зависимости ошибки оценки вероятности от надёжности этой оценки при различных значениях самой оценки вероятности и объёмов выборки, во-вторых, указать необходимые объёмы выборки для достижения приемлемых значений точности и надёжности оценки вероятности в практически значимых случаях. Эти результаты, несомненно, могут быть использованы в учебном процессе для формирования у студентов компетенции в области построения доверительных интервалов, недостаток которых отмечают многие источники.
Библиографическая ссылка
Краснощеков В.В., Семенова Н.В., Аббас А., Шбиб Х. ФОРМИРОВАНИЕ У СТУДЕНТОВ ВУЗА ПРЕДСТАВЛЕНИЯ О ТОЧНОСТИ И НАДЁЖНОСТИ ОЦЕНКИ ВЕРОЯТНОСТИ // Современные наукоемкие технологии. 2024. № 7. С. 163-170;URL: https://top-technologies.ru/ru/article/view?id=40102 (дата обращения: 03.02.2026).
DOI: https://doi.org/10.17513/snt.40102



