Введение
Графит является аллотропной модификацией углерода с атомной массой 12,0107 г/моль, плотностью 2,26 г/см3 и sp2-гибридизацией атомов углерода [1, с. 28]. Если к углеродным атомам графита присоединить атомы фтора, то sp2-гибридизация меняется на sp3-гибридизациию, но сохраняется гексагональная симметрия [2, с. 84]. Структура показана на рисунках 1а и 1б.
Если отщепить у графита один слой, то получается графен [3] (рис. 2а), а если отщепить один слой у фторографита, то получается фторографен [2, с. 84] (рис. 2б).
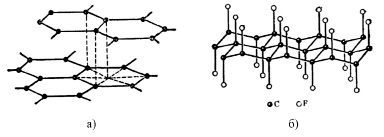
Рис. 1. Строение кристаллической решетки: графита (а); фторографита (б)
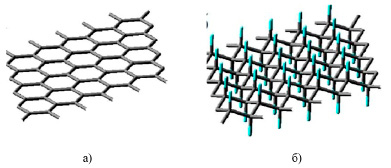
Рис. 2. Структура графена (а) и фторографена в конформации стула (б) [2]
В статье рассматривается фторид графита в форме СF0,96 [4], где определены: молекулярная масса М=30,2492 г/моль, плотность ρ=2,33 г/см3. Параметры решетки таковы [5, с. 30]: a=b=0,5034 нм; с=1,123 нм. Температуры плавления: для графита Tm=3650 К [6, с. 32]; для фторорафита Tm=773 К [7].
Цель исследования. В работе предлагается модель определения толщины поверхностного слоя графита и фторографита. Свойства поверхностного слоя определяют трибологические свойства пар трения, что является актуальным для многих отраслей промышленности. Модель пригодна и для любых конструкционных материалов.
Модель поверхностного слоя твердых тел
Поверхностный слой R(I) дается эмпирической формулой [8, 9]:
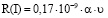[м] (1)
В уравнении (1) нужно знать один параметр – молярный объем элемента, который равен υ=М/ρ (М – молярная масса, ρ – ее плотность), α=1 м-2 – постоянная, чтобы соблюдалась размерность (R(I)=[м]). По формуле (1) рассчитаем R(I) (табл. 1) для графита и фторографита параллельно плоскости х=a=b и перпендикулярно этой плоскости х=с.
Эмпирически в работе [10] показано, что поверхностная энергия (ПЭ) γ2 равна:
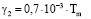[Дж/м2]. (2)
где Tm – температура плавления кристалла (К).
Размерный эффект в слое R(I) приводит к тому, что ПЭ становится равной γ1 [11]:
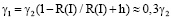. (3)
Из уравнения (3) следует, что ПЭ в слое R(I) в 3 раза меньше ПЭ основного кристалла. Чтобы снять слой R(I) от основного кристалла, нужно затратить энергию адгезии [12]:
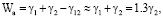(4)
где γ12 – ПЭ на границе раздела фаз, которая мала в силу фазового перехода II рода.
Таблица 1
Параметры R(I) = Lnm графита
|
Углерод |
М, г/моль |
ρ, г/см3 |
R(I)a, нм |
R(I)c, нм |
|
Графит |
12,0107 |
2,26 |
0,90 (3) |
2,46 (3) |
|
Фторографит |
30,2492 |
2,33 |
2,20 (4) |
6, 41 (4) |
Таблица 2
Упругие параметры графита, фторографита и графена, фторографена
|
Углерод |
Waа, мДж/м2 |
Waс, мДж/м2 |
σisа, МПа |
σisс, МПа |
Еа, ГПа |
Ес, ГПа |
|
Графит |
3613 |
1323 |
5740 |
1370 |
7,59 |
3,48 |
|
Фторографит |
541 |
180 |
24,94 |
3,11 |
2,53 |
1,16 |
|
Графен |
4160 |
– |
129000 |
– |
1000 |
– |
|
Фторографен |
610 |
– |
36852 |
286 |
– |
Внутренние напряжения σis между фазами γ1 и γ2 можно просчитать по формуле [12]:
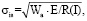(5)
где Е – модуль Юнга.
Используя уравнения (1) – (5), вычислим упругие параметры для графита и фторографита (табл. 2).
Результаты исследования и их обсуждение
Из таблицы 1 следует, что толщина поверхностного слоя у графита и фторографита меньше 10 нм и содержит 3–4 монослоя. Значит, она представляет собой наноструктуру. В работе [13] теоретически сделан вывод, что если такая структура включает в свой состав менее 6–8 слоев, то энергия квантовых состояний изменяется ступенчатым способом. Иными словами, поверхностный слой представляет собой квантовую наноструктуру при любой температуре.
Модуль Юнга у графита в 10÷100 раз меньше, чем у большинства металлов (табл. 3).
В таблице 2 приведены параметры для однослойных слоев – графена и фторографена – с использованием данных по модулю Юнга [14, с. 12, 15]. Из сказанного выше следует, что структура объемного кристалла выглядит следующим образом, как показано на рисунке 3а.
Таблица 3
Упругие параметры некоторых твердых металлов
|
Металл |
R(I), нм |
Wa, мДж/м2 |
εis, МПа |
Е, ГПа |
|
Au |
1.73 (4) |
1337 |
7813 |
79 |
|
Ag |
1.75 (4) |
1235 |
7665 |
83 |
|
Cu |
1.21 (3) |
1357 |
12000 |
110 |
|
Mn |
1.30 (2) |
1517 |
15199 |
198 |
|
Ni |
1.12 (3) |
1726 |
17776 |
207 |
|
Fe |
1.21 (4) |
1812 |
17550 |
211 |
|
Cr |
1.23 (4) |
2130 |
21977 |
279 |
|
Mo |
1.60 (5) |
2896 |
24413 |
293 |
|
W |
1.62 (5) |
3695 |
30611 |
371 |
На рисунках 3б и 3в показана зависимость физического свойства поверхностного слоя в виде [8]:
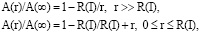(6)
где A(r) – физическое свойство нано- и мезослоя с координатой r; А(∞) – физическое свойство объемного образца (объемной фазы) (рис. 3а).
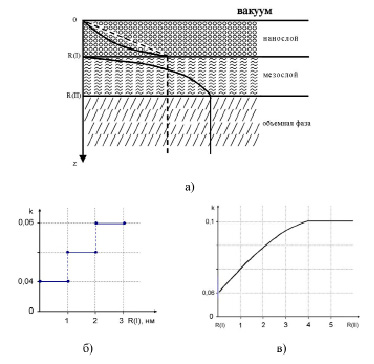
Рис. 3. Схема твердого тела: нанослой → мезослой → объемная фаза (а); зависимость коэффициента трения графита в нанослое (б) и в мезослое (в)
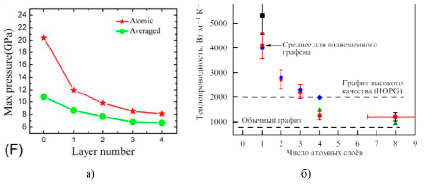
Рис. 4. Изменение максимального атомного напряжения (красная линия) и максимального среднего давления (зеленая линия) в зависимости от количества слоев графена (а) [16]; зависимость коэффициента теплопроводности пленок, составленных из нескольких графеновых слоев, от их числа (б) [17]
Здесь в качестве физического свойства взят коэффициент трения, который при движении графита (графена) по графиту (графену) при
1–R(I)/R(I)+r ≈ exp[–(R(I)/R(I)+r)]
будет в нанослое
k(r) = k(∞) exp[–(R(I)/R(I)+r)].
После этого трение в нанослое, то есть при r = 0 и при r = R(I), будет равно:
k(0) = k(∞) (1/e) = 0,1/2,72 = 0,04;
k[R(I)] = k(∞) (1/e1/2) = 0,1/1,65 = 0,06.
Здесь k(∞) = 0,1 для графита.
В результате в нанослое графита трение будет выглядеть с учетом работы [13] так, как показано на рисунке 3б. В мезослое трение будет зависеть по формуле 1 в уравнении (6), при этом 1-R(I) ≈ exp(-R(I)/r). Тогда k[R(I)] = k(∞) (1/e) (рис. 3а), и трение будет выглядеть так, как на рисунке 3в. У графита число монослоев в слое R(I) равно 3, а у фторографита равно 4. Это для графита подтверждается рисунком 4.
Оба рисунка наглядно показывают, что слой R(I) для графита содержит 3 слоя, что говорит о справедливости предложенной модели (1). Графен, содержащий более трех слоев, превращается в графит, и значения величин на рисунке 4 перестают зависеть от числа слоев.
У графена высокие внутренние напряжения σisа (табл. 2) приводят к «короблению» (рифлению) листов свободного графена (рис. 5) [18].
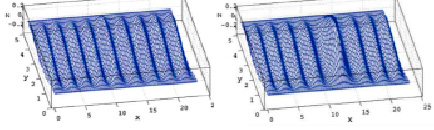
а) б)
Рис. 5. Морщины в графеновой наноленте зигзаг шириной N=20 и длиной M=100 с закрепленными краями (параллельно оси x) при деформации εxx= –εyy = –0,1, εxy=0,1 [18]
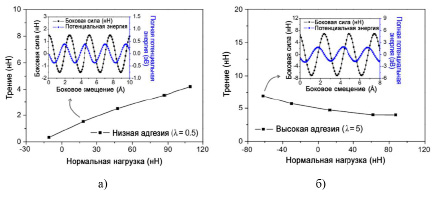
Рис. 6. Схема и типичный результат моделирования деформированной конфигурации для систем: с низкой адгезией (а); изменение силы трения Ff в зависимости от нормальной нагрузки. На вставке показано изменение боковой силы и потенциальной энергии как функция бокового смещения под действием нормальной нагрузки 18,3 нН; с высокой адгезией (б); изменение силы трения Ff в зависимости от нормальной нагрузки. На вставке показано изменение боковой силы и полной потенциальной энергии системы как функции бокового смещения при нормальной нагрузке −61,8 нН (б) [21].
В недавней работе [19] методом молекулярной динамики показано, что коробление графена, возможно, происходит из-за дислокационных диполей. Однако, на взгляд авторов, большие внутренние напряжения в графене возникают из-за большой величины модуля Юнга (формула (5) и табл. 2), который почти в 3 раза больше, чем у вольфрама (табл. 3). У фторографена и внутренние напряжения, и модуль Юнга в 3 раза меньше, чем у графена. Модуль Юнга у них близок к модулю Юнга молибдена (табл. 3). У фторографена энергия адгезии почти в 7 раз меньше, чем у графена (табл. 3). O.V. Penkov [20, с. 120] рассмотрел трибологические свойства графена и пришел к выводу, что ключевыми факторами, влияющими на трибологические свойства графена, являются энергия адгезии, количество слоев, режим укладки и материал подложки. Что касается количества слоев, то у графита и фторографита это количество почти одинаково, а вот энергии адгезии отличаются значительно. Это видно на рисунке 6.
Из рисунка 6 и таблицы 2 следует, что фторографен значительно превосходит графен по трибологическим свойствам и перспективен при его использовании в качестве модификатора трения для пластичных смазок [22, 23]. В работе [24] было экспериментально и теоретически для графена было показано, что с уменьшением числа слоев трение уменьшается. Это соответствует рисунку 3б и модели авторов (1). В работе [25, с. 132] показано, что даже малые деформации графена в пределах 10% достаточны для изменения его поверхности и его адсорбционных свойств. Если в таблице 2 взять для графена σisа за 100%, а для графита и фторографита σisа за х%, то при образовании графена и фторографена получается деформация графена 4,5%, а для фторографена – 0,06%. Это значит, что короблением фторографеновых листов можно пренебречь и трение у них минимально.
Когда графен сверху начинает двигаться по графиту, то в последнем при трении возникает турбулентный фрагмент, похожий на ячейки Бенара. Ячейки Бенара – это возникновение упорядоченности в виде конвективных ячеек в форме цилиндрических валов или правильных шестигранных фигур в слое вязкой жидкости с вертикальным градиентом температуры. А градиент температуры gradT ~ k, т.е. пропорционален коэффициенту внутреннего и внешнего трения, поэтому трение подобно вязкой жидкости.
Более строго при анализе процессов в системе Бенара в качестве управляющего параметра выбирается число Рэлея:
Re = gL3νa,
где g – ускорение свободного падения, L – характерный размер, b – коэффициент объемного расширения, dT – градиент температуры, ν – кинематическая вязкость, а – коэффициент температуропроводности среды. Поскольку кинематическая вязкость ν ~ 1/γ, γ – поверхностная энергия, то из приведенного выше выражения для числа Рэлея следует, что управляющим параметром в нашем случае является
Re ≈ C L3 γ,
где С ~ const, а L = R и 2γ = Wa.
Иными словами, если произведение R(I)•W(I)a для движущегося графена по поверхности графита меньше аналогичного произведения, то их разница, включая шероховатость трущихся материалов, равна [26, 2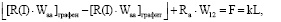7]:
(7)
где F – сила трения при движении трущихся материалов; Rа – шероховатость; L – длина пути движения; k – коэффициент трения; W12 – энергия адгезии между двумя материалами.
Уравнение (7) может служить критерием выбора антифрикционного покрытия из графена или из его композитов. Для графена в трении по графиту играет нанослой R(I), его трение происходит ступенчатым способом (рис. 3б).
Если трение графена, графита, фторграфена и фторграфита считать подобным трению вязкой жидкости, то следует, что трение зависит от скорости движения, имеет структуру, подобную ячейкам Бенара, а значит, происходят самоорганизация и синергизм трения. То, что трение углеродных структур нельзя объяснить с помощью обычного закона Амонтона или на основе гидродинамической теории смазки, обусловлено тем, что оно связано с вязкостью раствора (вязкой жидкости).
Жидкости, расплавы, плотная плазма и ряд других связанных систем, не имеющих упорядоченной структуры (в том числе и трущиеся поверхности), характеризуются неприятным для построения их теории свойством – средняя кинетическая энергия Е, приходящаяся на одну частицу, по порядку величины равна потенциальной энергии U. Из-за отсутствия малого параметра, по которому было бы удобно проводить разложение, не существует строгой теории применительно к жидкостям и расплавам, такой, как, например, к твердому телу (E/U << 1) или газу (E/U >> 1). Именно поэтому в настоящее время существует пять теорий, объясняющих процессы, происходящие при трении: механическая (деформационная); молекулярная (адгезионная); молекулярно-механическая; энергетическая; гидродинамическая.
Заключение
Развитие нанотрибологии сдерживалось тем, что толщину поверхностного слоя, ответственного за процесс трения, можно было определить только в высоком вакууме на атомарно-чистых поверхностях ограниченного числа монокристаллов. Модель, изложенная в настоящей статье, открывает новый подход в нанотрибологии. На основе этой модели показано, что у фторографеновых листов трение минимально и они могут быть использованы в качестве смазки, обладающей сверхсмазывающей способностью.
Библиографическая ссылка
Юров В.М., Жангозин К.Н., Гончаренко В.И., Олешко В.С. ТРИБОЛОГИЧЕСКИЕ СВОЙСТВА ГРАФИТА, ГРАФЕНА И ФТОРОГРАФИТА, ФТОРОГРАФЕНА // Современные наукоемкие технологии. – 2024. – № 7. – С. 81-87;URL: https://top-technologies.ru/ru/article/view?id=40089 (дата обращения: 21.11.2024).