Введение
В настоящее время технологический процесс невозможно представить без внедрения современных технологий. Целью внедрения данных технологий является поддержание технологических параметров в пределах, при этом минимизировать затраты на производство и максимизировать выход целевого продукта. Одним из инструментов, которые решают данные задачи являются системы усовершенствованного управления технологическим процессом (СУУТП), внедрение которых активно производится на многих предприятиях [1].
В основе СУУТП лежат многопараметрические регуляторы. Многопараметрические регуляторы предназначены для управления множеством технологических параметров одновременно. Эти регуляторы характеризуются тем, что имеют программную реализацию, то есть технологический процесс или его часть реализован в виде математической модели, блоков, с помощью которых просчитываются управляющие воздействия на процесс [2]. При этом в расчётах учитываются и непредсказуемые возмущения, которые так или иначе влияют на технологический процесс. Возможно соединение между созданными многопараметрическими регуляторами (субконтроллерами), что позволит полностью охватить каждый важный аспект технологического процесса [3]. Программная реализация позволяет внедрять их на все современные производства без затрат на закупку специализированного оборудования.
Целью исследования является исследование возможности реализации элементов систем усовершенствованного управления технологическим процессом на языке Python, а именно многопараметрического контроллера.
Материалы и методы исследования
В основе многопараметрического регулятора лежат передаточные функции, которые очень часто используются для описания линейных систем автоматического управления [4]. В качестве возможных реализаций передаточных функций на языке Python можно выделить:
− реализация аналитического решения;
− решение дифференциального уравнения;
− создание объекта класса Transfer function.
Реализация аналитического решения является наиболее простой и сводится к подстановке значений входного параметра в формулу [5].
Для решения дифференциальных уравнений на языке программирования Python реализованы множество методов, в данной работе будут рассмотрены следующие: Использование решателя SOLVE_IVP из библиотеки SCIPY [6]. В данном решателе реализованы следующие методы: RK45, RK23, DOP853, LSODA. Решатель ODEINT из библиотеки SCIPY использует алгоритм LSODA из библиотеки ODEPACK языка программирования Fortran.
В качестве критериев качества решения дифференциальных уравнений было решено использовать точность и скорость расчёта каждого метода. Для проверки каждого метода была создана выборка с различными показателями моделей первого и второго порядка, а также с различным временем симуляции.
Для реализации тестирования был создан скрипт, который случайным образом выбирает параметры модели первого порядка, замеряет время, за которое решается каждое дифференциальное уравнение.
Результаты исследования и их обсуждение
Результаты исследования показали, что самым быстрым и подходящим методом для решения дифференциальных уравнений для первого порядка является метод LSODA решателя SOLVE_IVP из библиотеки SCIPY. Вторым по скорости и точности вычислений является решатель ODEINT из библиотеки SCIPY. Метод DOP853 в виду образующихся колебаний во время решений имеет самые наибольшие показатели MSE и MAE среди всех.
В результате обработки полученных результатов для модели второго порядка можно отметить, что методы решения RK45, RK23 и DOP853 при симуляции не имеют колебания в конце в отличии от симуляции модели первого порядка. Однако данные методы значительно уступают в скорости решения. Лучшим методом для решения дифференциальных уравнений для моделей второго порядка является метод LSODA решателя solve_ivp из библиотеки scipy.
Третьим способом реализации передаточных функций на языке Python, как уже было отмечено ранее, является создание объектов класса Transfer function. Для создания объектов данного класса на языке Python можно воспользоваться одной из самых популярных библиотек CONTROL [7], использование которой позволяет реализовать основные операции для анализа и проектирования систем управления с обратной связью. К минусам данной реализации передаточной функции можно отнести отсутствие возможности создания передаточных функций с задержкой. Но и данный момент возможно реализовать, предусмотрев предварительную обработку входных сигналов.
Следующим этапом исследования является определение инструментов языка Python для вычисления оптимума и подборе параметров передаточной функции, а также подборе управляющих воздействий в предиктивном управлении. Особенностью данных задач является поиск оптимума целевой функции вместе с ограничениями искомых значений.
Для решения оптимизационных задач в языке Python большой популярностью пользуется модуль OPTIMIZE библиотеки SCIPY. Данный модуль позволяет определять локальные и глобальные экстремумы целевой функции, корни уравнений, подбирать значения параметров на основе квадратического отклонения и многое другое.
В рамках данного исследования будут использоваться следующие функции модуля OPTIMIZE: функции CURVE_FIT [8], MINIMIZE [9]. Для определения параметров целевой функции в CURVE_FIT реализованы следующие методы: Левенберга-Марквардта (lm), Trust Region Reflective (trf), dogbox. Для минимизации целевой функции c ограничениями в модуле MINIMIZE реализованы следующие методы: Nelder-Mead, L-BFGS-B, Powell, TNC, SLSQP, COBYLA, trust-constr.
Для идентификации математических моделей было создано GUI приложение. В качестве языка программирования для создания приложения был выбран также Python с использованием библиотеки customtkinter [10].
В качестве функциональных требований к разработанному приложению были определены следующие:
− возможность создания, сохранения и загрузки созданного пользователем проекта;
− возможность импорта внешних данных для идентификации моделей;
− возможность работы с графиками для импортируемых для анализа данных;
− возможность анализа корреляции между импортируемыми данными;
− возможность создания рассчитываемых переменных;
− возможность разделения данных на входные, промежуточные и выходные переменные;
− возможность выбора порядка передаточной функции, её реализации, оптимизатора и метода при идентификации модели;
− возможность наглядно оценить на графике и с отображением метрик полученные результаты подгонок.
Для определения наилучшего метода и реализации для идентификации моделей многопараметрического контроллера были подготовлены данные с реальных пошаговых тестирований на установках нефтеперерабатывающего завода при внедрении СУУТП и случайные сгенерированные данные. Для более объективного анализа было принято решение о разделении результатов тестирования, полученных на модели типа MV/CV и POV/CV. Связано это в первую очередь сложностью моделирования и подбора параметров моделей POV/CV, не каждое прикладное программное обеспечение, представленное на рынке способно подбирать подобного рода модели.
Исследования показали, что наилучшей реализацией передаточных функций на языке Python является аналитическое решение, ввиду простоты своей реализации. В частности, хорошо зарекомендовал себя оптимизатор CURVE_FIT с методами trf и dogbox, а также оптимизатор MINIMIZE с методами L-BFGS-B и SLSQP. При желании в дальнейшем использовать функционал библиотеки языка программирования Python CONTROL, возможно использование передаточной функции в виде объекта Transfer function с оптимизатором CURVE_FIT с методом dogbox. Наихудшей реализацией из представленных можно отметить реализация в виде дифференциальных уравнений с решателем SOLVE_IVP, что объясняется сложной реализацией для подбора параметров. Чуть лучше показал себя решатель ODEINT, но и он оказался не универсальным.
На сегодняшний день одним из самых популярных и распространённых методов регулирования параметров в промышленности является PID регулирование. Связано это с тем, что данный вид регуляторов имеет высокую надёжность работы в широком диапазоне, универсальность и прост в использовании и настройки.
Однако использование PID регулирования не позволяет учесть фактор возмущений, которые могут возникать на производстве. В связи с этим были брошены силы на исследование и разработку аналогов PID регуляторов. Так на производствах по всему миру началось внедрение так называемых контроллеров с прогнозирующим управлением (MPC – Model Predictive Control) – контроллеры с обратной связью, которые для прогнозирования и управления используют математическую модель технологического процесса. Именно при создании математической модели технологического процесса можно учесть всевозможные возмущения, которые могут оказываться на то тили иной параметр. Описание технологического процесса происходит с использованием передаточных функций.
Выделяют три временных периода при проектировании MPC контроллера: период прогнозирования – время, на которое MPC контроллером строится прогноз показаний параметров; период управления – время, которое отведено MPC контроллеру для планирования управления; период дискретизации – время, отработки MPC контроллера.
Особенностью MPC контроллера является результат его работы – он рассчитывает не одно управляющее воздействие, которое необходимо оказать на манипулируемые переменные (MV), а строит план оптимизации на весь заданный период управления. При этом в качестве заданий на манипулируемые переменные применяется только первое значение рассчитанного плана. На каждой итерации расчёта MPC контроллера, запуск которого задаётся с помощью периода дискретизации, план оптимизации строится заново.
В качестве примера MPC контроллера, который будет реализован в рамках исследования, было принято решение выбрать контур регулирования реальной СУУТП одного из нефтеперерабатывающего завода. Структура данного контура изображена на рисунке 1, все постоянные времени и задержки указаны в минутах. В качестве данных, на которых будет проводится тестирование, будут использованы значения с реального процесса за одни сутки.
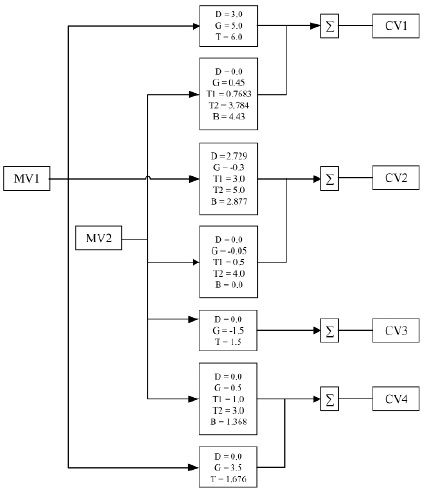
Рис. 1. Структура выбранного для исследования контура
Выбранный контур контроллера СУУТП имеет следующие свойства:
− период прогнозирования контроллера 10 минут;
− период управления контроллера 30 секунд;
− период дискретизации контроллера 30 секунд;
− MV1 – положение клапана, который в СУУТП имеет вес равный 3.315969. В суточных данных оперативным персоналом установлена верхняя граница по данному параметру равной 40, нижняя – 19;
− MV2 – положение клапана, который в СУУТП имеет вес равный 0.005068. В суточных данных оперативным персоналом установлена верхняя граница по данному параметру равной 70, нижняя – 25;
− CV1 – температура, которая в СУУТП имеет вес равный 1, а также имеет 1 приоритет. В суточных данных оперативным персоналом установлена верхняя граница по данному параметру 905, нижняя – 0;
− CV2 – содержание некоторого вещества, которое в СУУТП имеет вес равный 5, а также имеет 2 приоритет. В суточных данных оперативным персоналом установлена верхняя граница по данному параметру 5.8, нижняя – 5.5;
− CV3 – давление, которое в СУУТП имеет вес равный 1, а также имеет 2 приоритет. В суточных данных оперативным персоналом установлена верхняя граница по данному параметру 31, нижняя – 22;
− CV4 – температура, которая в СУУТП имеет вес равный 1, а также имеет 1 приоритет. В суточных данных оперативным персоналом установлена верхняя граница по данному параметру 1080, нижняя – 0.
Стоит отметить, что чем выше приоритет у контролируемой переменной по отношению к другим, тем более важной она является для контроллера СУУТП. В ситуации, когда контролируемые переменные находятся вне границ регулирования, первоочередной задачей контроллера СУУТП является определение воздействий на манипулируемые переменные, которые позволят обеспечить нахождение в границах контролируемых переменных с наивысшим приоритетом.
Перед тем, как проводить расчёты на сконструированном контуре необходимо протестировать правильность и адекватность предсказаний по контролируемым переменным, которые делает контур, изменяя манипулируемые переменные. Для этого тестирования было принято решать обратную задачу – в качестве уставок на манипулируемые переменные будут использованы данные работы реального СУУТП, а затем сравнить предсказанные моделью значения и фактические значения технологического процесса. Для проведения данного тестирования был создан скрип, результаты которого представлены рисунке 2.
Как видно из рисунка 2 наибольшей абсолютной ошибкой обладает контролируемая переменная CV3, связано это в первую очередь с большими колебаниями показания датчика давления. В целом, можно считать, что предсказания, которые делает модель контура, верные.
Для реализации MPC контроллера на языке Python был создан скрипт, который принимает данные с технологического процесса и рассчитывает оптимальные изменения манипулируемых переменных MV1 и MV2. В качестве оптимизатора был использован MINIMIZE, а для реализации передаточных функций библиотека CONTROL, использование которой позволит сделать более удобной конструирование выбранного контура СУУТП. В качестве входных параметров данного скрипта являются данные контролируемых переменных, их границы и другие параметры контроллера, а в качестве выходных переменных – задания на управляемые переменные.
Результаты тестирования, разработанного MPC контроллера на суточных данных следующие:
− процент совпадения направленности расчётов – 73%;
− процент успешного расчёта – 98%;
− среднее время расчёта – 23 секунды.

Рис. 2. Средние абсолютные ошибки
По результатам тестирования видно, что разработанный MPC контроллер время имеет большое время расчёта, связано это в первую очередь с созданием передаточных функций с использованием библиотеки CONTROL, которую можно заменить на аналитическое решение. Также по результатам тестирования видно, что разработанный MPC контроллер имеет высокий процент успешного расчёта – рассчитанный план управления по прогнозам обеспечит нахождение контролируемых переменных в границах регулирования.
По результатам тестирования также оценён процент совпадения направленности расчётов с существующим контроллером СУУТП. Оценка именно направленности расчётов обусловлена тем, что существующий контроллер СУУТП решает задачу нахождения минимума целевой функции всего контроллера, а не отдельного контура управления. Следовательно, достичь результатов существующего контроллера СУУТП без учёта остальных контуров контроллера невозможно. Однако стоит отметить, что разработанный MPC контроллер имеет высокий процент совпадения направленности расчётов с существующим контроллером СУУТП.
На основании анализа результатов тестирования можно сделать вывод об успешности разработанного MPC контроллера.
Заключение
В основе СУУТП лежат многопараметрические регуляторы с прогнозирующим управлением, структуры которых определяются при внедрении СУУТП. В многопараметрических регуляторах для построения прогнозов по контролируемым переменным используются передаточные функции.
На этапе проектирования создаваемых модулей на языке Python были определены 3 варианта реализации передаточных функций, а также выбраны оптимизаторы, с помощью которых производилась идентификация и многопараметрическое управление. В ходе тестирования модуля идентификации моделей были определены реализации, а также оптимизаторы, наиболее подходящие для данной задачи.
В ходе разработки MPC контроллера был выбран контур реально функционирующей СУУТП, а также были получены данные работы данного контура. На основе полученных данных было проведено тестирование разработанного алгоритма и сделаны выводы об успешности данного решения.
Библиографическая ссылка
Вотякова Л.Р., Зотин А.В. ИССЛЕДОВАНИЕ ИДЕНТИФИКАЦИИ И РЕАЛИЗАЦИИ МНОГОПАРАМЕТРИЧЕСКОГО КОНТРОЛЛЕРА НА ЯЗЫКЕ PYTHON // Современные наукоемкие технологии. 2024. № 7. С. 16-21;URL: https://top-technologies.ru/ru/article/view?id=40079 (дата обращения: 04.02.2026).
DOI: https://doi.org/10.17513/snt.40079



