В методе муравьиных колоний ACO (ant colony optimization) [1] искусственная муравьиная колония имитирует поведение настоящих муравьев, идущих по феромонным следам. Перемещение муравьев и формирование феромонного следа осуществляется на графе. Искусственные муравьи перемещаются по дугам графа, поочередно посещая различные объекты – вершины графа. Искусственный феромон, соответствующий записи маршрутов, пройденных муравьиной колонией, накапливается во время выполнения программы с помощью механизма обучения. Отдельные муравьи одновременно собирают необходимую информацию, стохастически принимают собственные решения и независимо строят решения в пошаговой процедуре. Информация, необходимая для принятия решения на каждом шаге, включает в себя концентрацию феромона, данные о задаче и значения эвристических функций. Феромон, отложенный на пути, принадлежащем лучшему решению итерации, будет положительно увеличен, чтобы стать более привлекательным в последующих итерациях. Благодаря коллективному поведению ACO может эффективно решать широкий класс задач комбинаторной оптимизации.
Первоначально алгоритм ACO может разрабатывался для решения задачи коммивояжера [1]. Его решение можно записать следующим образом:
1. Инициализация феромонов. Для каждого ребра графа инициализируются значения феромона. Обычно начальные значения выбираются одинаковыми или случайными.
2. Инициализация. Создаются муравьи, которые будут перемещаться по графу для нахождения оптимального пути. Начальное состояние создается путем размещения муравьев на случайных вершинах графа (города) коммивояжера.
3. Выбор пути:
- Каждый муравей начинает свой путь из своей начальной вершины. В цикле муравей должен посетить все вершины графа (алгоритм коммивояжера)
- На каждом шаге цикла муравей выбирает следующий узел согласно вероятностям, основанным на феромоне и других характеристиках графа (1).
- Выбор следующего узла возможен только из тех, в которых муравей еще не побывал, и в те, в которые из текущей вершины имеются дуги.
Выбор определяется путем определения конкретного события (генерация какое событие произойдет) исходя из распределения вероятностей (1):
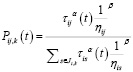 , (1)
, (1)
где t – номер итерации; ij – дуга из вершины i в вершину j; k – номер муравья-агента; Ji,k – дуги, по которым может переместиться k муравей-агент из вершины i; α > 0, β > 0 – степенные параметры мультипликативной свертки. В (1) присутствует как информация, обратная длине дуги (1 / ηij) > 0, так и величина феромонного следа на дуге τij ≥ 0.
4. Обновление феромонного следа:
- После того как все муравьи завершили свои пути, феромонный след обновляется.
- Феромонный след (феромон) на каждой дуге усиливается и испаряется в зависимости от эффективности муравьев, прошедших этот путь.
Обновление феромонов происходит по формуле
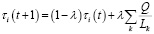 , (2)
, (2)
где t – номер итерации; Lk – длина пути k муравья-агента; Q > 0 – параметр метода муравьиных колоний; λ ∈ (0..1) – параметр метода муравьиных колоний..
5. Повторение: Шаги выбора пути и обновления феромона повторяются заданное количество раз или до тех пор, пока не будет достигнут критерий останова.
6. Лучшее решение. В конце выполнения алгоритма выбирается лучший маршрут из всех найденных муравьями маршрутов.
7. Завершение. Возвращение лучшего маршрута в качестве решения задачи коммивояжера.
Этот процесс повторяется несколько раз, пока не будет достигнуто удовлетворительное решение или не будет пройдено определенное количество итераций. Благодаря коллективной работе муравьев и учету феромонов, алгоритм ACO может находить оптимальные или близкие к оптимальным решениям для задачи коммивояжера.
Целью работы было рассмотреть эффективность применения метода муравьиных колоний для кластеризации объектов, исследовать влияние параметров метода на метрики кластеризации: схожесть между двумя кластеризациями, коэффициент силуэта, нормализованный индекс взаимной информации и коэффициент Фаулкса-Маллова, а также по результатам исследования предположить применение метода муравьиных колоний для кластеризации пассажирских авиатранспортных маршрутов.
Материалы и методы исследования
Современные разработки в области муравьиных колоний [1] уже решают задачи подбора параметров для решателей на основе нейронных сетей и систем машинного обучения. С помощью специальных структур графов метод муравьиных колоний легко расширяется на задачи составления расписаний [2, 3], задачи классификации [4], управления поставками [5] и задачи о назначении [6, 7]. В работе рассматривается задача кластеризации и ее решение с помощью метода муравьиных колоний. Данная задача рассматривалась сообществом исследователей, и были получены методы ACOC (ACO-Based Clustering) [8] и MACOC (Medoid-Based ACO Clustering) [9]. В работе рассматривается эффективность предложенных методов, определяются рациональные значения параметров алгоритма. Предложенные исследования позволяют применять данные алгоритмы для классификации пассажирских авиационных маршрутов.
С помощью использования особенностей алгоритма ACO, муравьиный алгоритм можно использовать и для кластеризации объектов. Алгоритм ACOC в основном опирается на феромонные тропы, по которым муравьи выбирают кластер для каждого объекта данных [8]. Значение тропы, τij, в узле (i, j) представляет собой концентрацию феромонов объекта i, связанного с кластером j. В алгоритме муравьи последовательно посещают объекты данных, один за другим, и выбирают кластеры для объектов данных, учитывая не только информацию о феромонах и расстояние от объекта до центроида. Центроид пересчитывается по формуле (3), аналогичной методу машинного обучения k-means, но пересчет координат центроида осуществляется в конце итерации, после того как N муравьев-агентов определили свои маршруты.
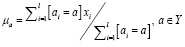 (3)
(3)
где a – номер кластера; Y – множество всех возможных кластеров; μa – координаты центройда для кластера a; l – объем выборки, количество объектов; i – номер объекта; [ai = a] – выбор i-го объекта к кластеру a; xi – значение параметров i-го объекта.
Оценка качества кластеризации, например: Средняя внутрикластерная плотность, Силуэтный коэффициент (Silhouette Coefficient), Внутригрупповая дисперсия (Within-cluster sum of squares, WCSS), Индекс Дэвиса – Болдуина (Davies-Bouldin Index), Индекс Калински – Харабаса (Calinski-Harabasz Index) могут использоваться как целевая функция Lk в методе муравьиных колоний. Задачей метода муравьиных колоний будет минимизация целевой функции. Для вычисления оценок необходимо задаться метрикой определения расстояния между объектами. В работе применяется метрика Минковского, введенная в математическом анализе и геометрии, является фундаментальным инструментом в измерении расстояний между точками в n-мерном пространстве. Это обобщение евклидовой и манхэттенской метрик, позволяющее учитывать различные степени взаимного влияния отклонений по каждому измерению на общее расстояние.
Перемещение муравьев-агентов происходит по графу специальной структуры, параметрический граф (рис. 1). В параметрическом графе каждому объекту назначается набор вершин, определяющих кластеры. Выбор одной из вершин определяет конкретный кластер для данного объекта. Порядок вершин неважен.
Параметры, влияющие на работу алгоритма:
1. Число муравьев на итерации N. Это количество агентов, которые исследуют пространство кластеров. Большее количество муравьев может увеличить вероятность обнаружения лучших решений, но может также повысить вычислительную сложность алгоритма.
2. Число элитных муравьев на итерации M. Это те муравьи, которые достигли наилучшего или одного из лучших решений в текущей итерации. Количество элитных муравьев определяет, сколько из лучших решений будет использоваться для обновления феромонов.
3. Число кластеров Y. Это количество кластеров, на которые разбивается набор данных. Выбор оптимального числа кластеров является важным шагом, так как это влияет на качество кластеризации.
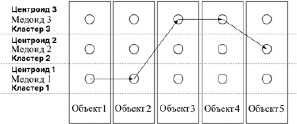
Рис. 1. Структура параметрического графа для решения задачи классификации методом муравьиных колоний
4. Параметры феромонов.
5. Начальные значения феромонов τi(0). Это значение, с которого начинается процесс обновления феромонов. Обычно выбирают небольшие одинаковые значения, чтобы избежать предвзятости.
6. Скорость испарения феромонов λ. Это коэффициент, определяющий скорость исчезновения феромонов со временем. Он влияет на степень сохранения информации о маршрутах муравьев.
7. Параметры эвристики. Это параметры, которые помогают муравьям принимать решения на каждом шаге. Это расстояние между объектами в пространстве кластеров, вероятность выбора стратегии.
8. Количество итераций. Это количество циклов, в течение которых муравьи перемещаются по объектам.
Задача кластеризации алгоритмом ACO-Based Clustering сводится к выполнению аналогичных оригинальному алгоритму шагов:
1. Инициализация феромонов. Элементы матрицы феромонов устанавливаются на произвольно выбранные малые значения (τi(0)).
2. Построение решений, кластеризация объектов. Для каждого муравья-агента построение решения начинается с выбора случайного объекта и его ассоциация с кластером (4). Затем муравей перемещается по пространству объектов, выбирая кластеры для остальных объектов. Выбор кластера осуществляется с использованием правил, основанных на феромонах и эвристиках: муравьи выбирают одну из стратегий, которое определяется в результате сравнения сгенерированного равномерно распределенного на интервале (0..1) числа и заранее определенной вероятности q0:
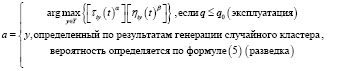 (4)
(4)
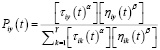 , (5)
, (5)
где α – параметр влияния феромонного следа; β – параметр влияния меры привлекательности; q0 – параметр, определяющий вероятность выбора стратегии эксплуатации или разведки, в случае эксплуатации муравей-агент выберет самый лучший для текущего объекта вариант; Piy(t) – вероятность, с которой выбирается кластер y для объекта i на итерации t, применяется в случае разведки; τiy(t) – количество феромонного следа для кластера y для объекта i на итерации t; ηiy(t) – значение целевой функции (например, величина средней внутрикластерной плотности) для кластера y для объекта i на итерации t, данная величина, в отличие от длин дуг графа в алгоритме коммивояжера данное значение изменяется на каждой итерации; Y – общее количество кластеров.
3. Обновление феромонного следа. После того как каждый муравей завершил построение решения, обновляются значения феромонов на ребрах графа. Это делается с учетом качества построенных кластеров. Чем лучше кластеризация с точки зрения целевой функции, тем больше феромонов добавляется.
4. Повторение итераций. Шаги 2–4 повторяются до тех пор, пока не будет выполнено достаточное количество итераций.
5. Выбор лучшего решения. После завершения всех итераций выбирается лучшее найденное решение, которое является результатом кластеризации.
Модифицированный алгоритм кластеризации MACOC (Medoids Ant Colony Optimization for Clustering) основан на ACOC, но вместо центроидов использует медоиды [9]. Медоид – это центральный объект или «представитель» кластера в задаче кластеризации. Он представляет собой объект данных, который имеет наименьшую сумму расстояний до всех остальных объектов в кластере. Медоид может быть рассмотрен как «типичный» представитель кластера, который лучше всего описывает его структуру. В отличие от центроида, который является средним значением всех объектов в кластере, медоид является фактическим объектом данных из кластера. В задаче кластеризации использование медоидов как центральных точек кластеров может улучшить интерпретируемость и стабильность решения. Муравей посещает каждый объект, чтобы отнести его к медоиду на основе эвристической информации и уровня феромонов. При движении муравьев-агентов каждый муравей случайно выбирает точки, которые будут медоидами. Они перемещаются между точками данных, выбирая для текущей точки соответствующий медоид на основе вероятностной функции, которая учитывает количество феромонов на ребрах между текущей точкой данных и каждым медоидом, а также длину этого ребра.
Одно из основных различий между ACOC и MACOC заключается в том, что MACOC хранит больше информации о перемещениях муравьев в матрице феромонов [9]. В случае ACOC матрица феромонов – это связь между экземпляром и меткой центроида, которая не является самим центроидом. В случае MACOC матрица феромонов является связью между экземпляром и медоидом (другим объектом данных), а это означает, что если в результате случайного выбора медоид-метка изменится, то предыдущее значение феромонов останется более объективным, нежели значение феромонов между объектами и меткой центроида, которую вновь пересчитали.
Результаты исследования и их обсуждение
Работа алгоритма исследовалась на датасете make_moons из библиотеки scikit-learn. Датасет make_moons представляет собой набор данных, который генерирует два полукруга, образующих два класса, каждый класс имеет одинаковое количество точек и нормально распределенные шумы. Данный датасет плохо кластеризуется методами k-means, и поэтому исследование близких алгоритмов ACOC и MACOC является наиболее интересным. В результате проведения экспериментов проанализированы ключевые метрики, включая adjusted_rand_score (схожесть между двумя кластеризациями), silhouette_score (коэффициент силуэта), normalized_mutual_info_score (нормализованный индекс взаимной информации) и fowlkes_mallows_score (коэффициент Фаулкса – Маллова) (рис. 2).
В ходе исследования были подвергнуты анализу различные параметры, влияющие на производительность и эффективность алгоритма. Среди этих параметров выделяются:
− statistic_n_iter: количество итераций метода муравьиных колоний;
− count_ants: количество муравьев, участвующих в поиске решения;
− count_elitist_ants: количество элитных муравьев, которые оставляют феромон на своем пути;
− alpha и beta: коэффициенты, определяющие влияние феромона и привлекательности соответственно на выбор следующего шага муравья;
− init_pher: начальное количество феромона на каждом ребре;
− n_iter: количество итераций, проводимых алгоритмом;
− p: коэффициент испарения феромона между итерациями;
− q: вероятность проведения случайного перемещения муравьем;
− r_minkovsky: параметр метрики Минковского, который определяет степень ее чувствительности к различиям в признаках.
Анализ указанных параметров был направлен на выявление их влияния на качество кластеризации и скорость сходимости алгоритма. Различные значения параметров были рассмотрены и протестированы на датасете make_moon, что позволило выявить оптимальные конфигурации для алгоритма муравьиной колонии с Минковской метрикой.
На рис. 2 показаны шесть графиков, иллюстрирующих статистики и метрики качества кластеризации для муравьиного алгоритма в зависимости от числа итераций (параметр statistic_n_iter). Результаты для k-means обозначены пунктирной линией, а красная сплошная линия представляет интерполяцию результатов для муравьиного алгоритма.
На верхнем левом графике отображено время выполнения алгоритма, которое линейно увеличивается с ростом числа итераций. Это закономерное поведение, поскольку увеличение числа итераций требует больше вычислительных ресурсов и времени.
Верхний правый график показывает значения критерия adjusted_rand_score, измеряющий схожесть между двумя кластеризациями. Синяя линия демонстрирует колебания этого показателя для муравьиного алгоритма, но в целом видна тенденция к улучшению по мере увеличения числа итераций. Пунктирная линия, представляющая результат для k-means, остается стабильной, но ниже, чем у муравьиного алгоритма.
Средний левый график показывает значение целевой функции в зависимости от количества итераций. Синяя линия показывает, что целевая функция муравьиного алгоритма уменьшается и стабилизируется. Это говорит о том, что дальнейшее увеличение количества итераций не приносит явного улучшения и только увеличивает время выполнения алгоритма.
На нижнем левом графике представлен коэффициент силуэта (silhouette_score), который измеряет качество кластеров. Видно, что значение silhouette_score для муравьиного алгоритма увеличивается с числом итераций и приближается к результатам k-means, которые остаются стабильными.
Средний правый график демонстрирует нормализованный индекс взаимной информации (normalized_mutual_info_score). Синяя линия показывает, что этот показатель для муравьиного алгоритма постепенно растет и стабилизируется, приближаясь к результату k-means, который ниже и стабилен.
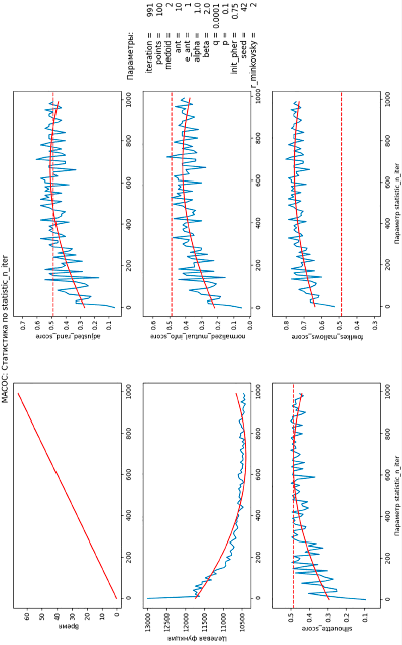
Рис. 2. Анализ влияния количества итераций алгоритма MACOC на различные метрики качества кластеризации
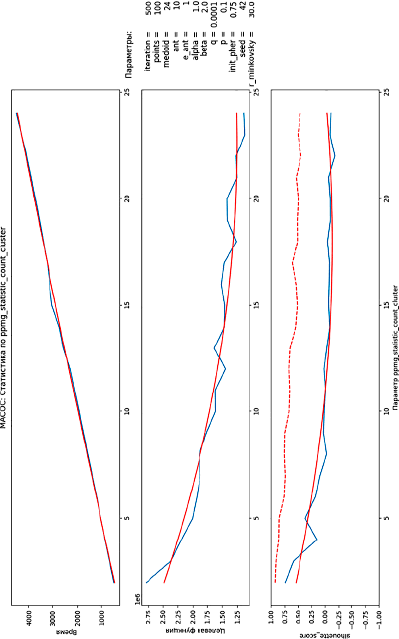
Рис. 3. Анализ эффективного количества кластеров при кластеризации пассажирских авиационных маршрутов
Нижний правый график иллюстрирует коэффициент Фаулкса – Маллова (fowlkes_mallows_score), оценивающий точность кластеризации. Значение этого показателя для муравьиного алгоритма со временем увеличивается и постепенно приближается к результату k-means.
Таким образом, графики показывают, что муравьиный алгоритм демонстрирует улучшение по большинству метрик с увеличением числа итераций, постепенно достигая или даже превышая качество кластеризации, достигаемое методом k-means.
Среди аналогичных исследований значений параметров приведем пример влияния параметров на коэффициент силуэта (silhouette_score):
− Изначально увеличивается по мере увеличения alpha, что указывает на улучшение кластеризации. Однако после достижения максимального значения около alpha = 1.5, silhouette_score начинает снижаться, что говорит о том, что дальнейшее увеличение alpha отрицательно влияет на качество кластеризации.
− Увеличивается по мере увеличения beta, но после достижения максимального значения около beta = 1.2 silhouette_score выходит на плато, что говорит о том, что дальнейшее увеличение beta не влияет на качество кластеризации.
− Аналогично увеличивается по мере увеличения количества муравьев-агентов на итерации (count_ants). При достижении count_ants = 3 silhouette_score выходит на плато, что говорит о том, что дальнейшее увеличение count_ants не влияет на качество кластеризации.
− Практически не изменен по мере увеличения количества элитных муравьев (count_elitist_ants).
− При увеличении параметра метрики Минковского (r_minkovsky) до 30 показатель не изменяется, но после ухудшает кластеризацию.
Одним из перспективных применений метода кластеризации на основе муравьиных колоний является кластеризация авиационных пассажирских маршрутов между городами. Для реализации данного метода требуется информация, характеризующая каждый отдельный пассажиропоток. Эта информация может включать такие параметры, как количество пассажиров в месяц, расстояние между городами и длительность рейса.
На рис. 3 отображена зависимость метрик от количества кластеров, на которые разбиваются авиационные пассажирские маршруты. На нижнем графике рис. 3 можно наблюдать, что наилучшее качество кластеризации достигается при количестве кластеров, равном 2, 3 и 5. При любом другом количестве кластеров датасет распределяется более равномерно, что свидетельствует о менее четкой сегментации данных.
Заключение
Можно отметить, что успешная реализация методов оценки качества кластеризации является ключевым фактором для повышения эффективности и точности кластерных анализов. Рассмотренные метрики, такие как силуэтный коэффициент, индекс Дэвиса – Болдуина, внутригрупповая дисперсия, индекс Калински – Харабаса и средняя внутрикластерная плотность, играют значимую роль в прикладных задачах. Использование этих метрик в качестве целевой функции в методах муравьиных колоний способствует оптимизации кластерных структур и обеспечивает достижение более надежных и интерпретируемых результатов.
На основе этих характеристик метод муравьиных колоний способен выявлять кластеры пассажиропотоков, что позволяет выделить группы схожих по своим параметрам перемещений. Это, в свою очередь, может способствовать оптимизации транспортных систем, улучшению планирования инфраструктуры, повышению качества обслуживания пассажиров и снижению затрат на транспортные услуги, а также дает возможность подобрать необходимый самолет для одного из кластеров или заменить его на похожий по характеристикам.
Библиографическая ссылка
Судаков В.А., Кильмишкин Н.В., Титов Ю.П. ПРИМЕНЕНИЕ МОДИФИКАЦИИ МЕТОДА МУРАВЬИНЫХ КОЛОНИЙ ДЛЯ КЛАССИФИКАЦИИ АВИАТРАНСПОРТНЫХ МАРШРУТОВ // Современные наукоемкие технологии. 2024. № 6. С. 63-70;URL: https://top-technologies.ru/ru/article/view?id=40065 (дата обращения: 14.02.2026).
DOI: https://doi.org/10.17513/snt.40065



