Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Гусарова О.М. 1 Денисов Д.Э. 1

---

1 ФГОБУ ВО «Финансовый университет при Правительстве Российской Федерации»

Целями исследования являются обобщение и систематизация методологических подходов и методики оценки качества математических моделей для решения широкого круга прикладных задач с использованием современных цифровых технологий. В ходе исследования использовались методы математической статистики и теории вероятностей, метод статистических наблюдений и выборочных совокупностей, методы стохастического моделирования, базирующиеся на аппарате корреляционно-регрессионного анализа. Статистические расчеты и анализ полученных результатов выполнены в среде SPSS Statistics. В качестве информационной базы для построения математических моделей использовались официальные статистические данные социально-экономического развития региональных субъектов в интервале 2010–2022 гг. В ходе исследования рассмотрены общесистемные подходы к построению многофакторных регрессионных моделей, выполнен обзор основных принципов построения системы факторов-регрессоров. Систематизированы критерии оценки качества регрессионных моделей. Приведены математические зависимости оценки критериев исследования качества проектируемых моделей. Обозначены рекомендуемые интервалы для определения статистической значимости регрессионных уравнений и факторов-регрессоров. Приведены фрагменты программирования для реализации функций корреляционно-регрессионного анализа в среде SPSS Statistics. Выполнены расчеты и обоснование результатов корреляционной зависимости и регрессионной статистики при построении математических моделей для показателей уровня развития регионального субъекта. Практическая значимость исследования заключается в возможности применения результатов исследования при разработке стратегий развития региональных субъектов на краткосрочную и долгосрочную перспективу с использованием математического моделирования и современных цифровых технологий.

Статья в формате PDF

478 KB

математические модели

многофакторная регрессия

критерии оценки качества регрессионных уравнений

1. Указ Президента Российской Федерации от 07.05. 2024 № 309 «О национальных целях развития Российской Федерации на период до 2030 г. и на перспективу до 2036 года». URL: http://publication.pravo.gov.ru/document/0001202405070015?ysclid=lxa7zi8vdo7775326 (дата обращения: 11.04.2024).

2. Гусарова О.М., Денисов Д.Э., Сулеменков А.В. Математическое моделирование и численные методы оценки эффективности малого и среднего бизнеса // Современные наукоемкие технологии. 2023. № 10. С. 32-38. DOI: 10.17513/snt.39788.

3. Гусарова О.М., Денисов Д.Э. Цифровые трансформации как фактор стимулирования развития бизнеса // Фундаментальные исследования. 2022. № 5. С. 40-45. DOI: 10.17513/fr.43251.

4. Орлова И.В. Оценивание параметров регрессионной модели с помощью ковариаций переменных и интерпретация коэффициентов регрессии // Мягкие измерения и вычисления. 2023. Т. 71, № 10-1. С. 5-12.

5. Зададаев С.А., Орлова И.В. Опыт применения эконометрического инструментария для прогнозирования показателей национальных целей развития РФ // Фундаментальные исследования. 2022. № 10-1. С. 54-59. DOI: 10.17513/fr.43343.

6. Орлова И.В. К вопросу об оценке качества эконометрических моделей // Фундаментальные исследования. 2022. № 3. С. 92-99. DOI: 10.17513/fr.43220.

7. Росстат. Официальный сайт Федеральной службы государственной статистики. [Электронный ресурс]. URL: https://rosstat.gov.ru/ (дата обращения 25.04.2024).

В стратегии развития Российской Федерации до 2030 года и на перспективу до 2036 года основными целями национального развития отечественной экономики являются «укрепление экономического суверенитета, увеличение численности населения страны и повышение уровня жизни граждан» [1, с. 1]. Авторы настоящей публикации в более ранних научных трудах исследовали динамику ряда показателей уровня развития ряда региональных субъектов [2, 3]. В ходе проведенных исследований с целью выявления тенденций развития хозяйствующих субъектов были построены математические модели, характеризующие особенности развития региональных субъектов. При этом систематически возникал вопрос об уровне надежности и достоверности построенных математических моделей и степени доверия к полученным результатам исследования.

Целями исследования являются обобщение и систематизация методологических подходов и методики оценки качества математических моделей для решения широкого круга прикладных задач с использованием современных цифровых технологий.

Материалы и методы исследования

При проведении исследования в качестве материалов использовались статистические данные по показателям социально-экономического развития региональных субъектов в интервале 2010–2022 гг.

Для получения достоверных результатов применялись методы математической статистики и теории вероятностей, метод статистических наблюдений и выборочных совокупностей, методы стохастического моделирования с использованием инструментария корреляционно-регрессионного анализа. Статистические расчеты и анализ полученных результатов осуществлялись в среде SPSS Statistics.

Результаты исследования и их обсуждение

Для построения математических моделей показателей социально-экономического развития региональных субъектов представляется целесообразным использование инструментария корреляционно-регрессионного анализа, базирующегося на методах математической статистики и теории вероятностей.

Для оценки уровня социально-экономического развития регионального субъекта может быть использована многофакторная регрессионная модель, которая может быть записана в общем виде:

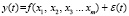, (1)

где y(t) – значение результативного признака, характеризующего уровень социально-экономического развития регионального субъекта;

f – функция зависимости результативного признака и экзогенных факторов-регрессоров;

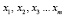– набор экзогенных факторов-регрессоров;

ε(t) – стохастическая компонента, характеризующая различного рода технические погрешности и влияние случайных факторов.

Определение параметров уравнения множественной линейной регрессии может быть осуществлено с использованием метода наименьших квадратов. Важным моментом при осуществлении спецификации модели является построение системы показателей для выбора факторов-регрессоров. При этом необходимо провести оценку корреляционных зависимостей между эндогенной переменной и экзогенными факторами-признаками.

Корреляционная матрица имеет вид:

, (2)

где ryxi – коэффициент корреляции, характеризующий влияние соответствующего фактора-регрессора на зависимую переменную;

rxixj – коэффициент парной корреляции между экзогенными переменными, рассматриваемыми в качестве факторов-регрессоров, оценивающий величину их взаимного влияния [4].

Для определения величины коэффициента парной корреляции между результативным признаком и фактором-регрессором может быть также использована формула:

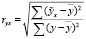, (3)

где 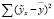– сумма квадратов отклонений моделируемых значений результативного признака, обусловленная влиянием фактора-регрессора, от среднего значения y, рассчитанного по эмпирическим данным;

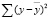– общая сумма квадратов отклонений эмпирических значений признака y относительно его среднего значения.

Метод наименьших квадратов позволяет определить параметры модели регрессии. В общем случае нахождение параметров множественной регрессии сводится к нахождению минимума функции G, характеризующей сумму отклонений эмпирических данных от моделируемых значений результативного признака с использованием регрессионной модели:

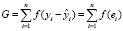, (4)

где f – функция, характеризующая математическую форму измерения разброса эмпирических данных относительно моделируемых значений. В большинстве случаев в качестве математической формы используется квадрат разброса эмпирических и моделируемых значений результативного признака.

После осуществления этапа параметризации регрессионной модели необходимо осуществить исследование качества и достоверности разработанной регрессионной модели. С этой целью необходимо провести анализ ряда следующих характеристик.

Для оценки общего качества уравнения регрессии традиционно используется коэффициент детерминации, значение которого может быть определено по формуле:

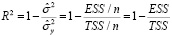, (5)

где

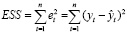(6)

– величина дисперсии остатков, характеризующих отклонения фактических и расчетных (моделируемых) значений эндогенной переменной;

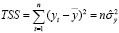(7)

– величина общей дисперсии, характеризующей величину отклонений фактических значений признака-результата относительно среднего значения результативного признака.

Значение коэффициента детерминации может изменяться в пределах [0–1], и, чем ближе его значение к 1, то есть чем меньше соотношение остаточной и общей дисперсии, тем более высоким признается общее качество построенного уравнения регрессии.

Для оценки статистической значимости уравнения регрессии и достоверности полученных результатов рекомендуется использовать величину F-критерия Фишера, значение которого может быть рассчитано как отношение факторной и остаточной дисперсии результативного признака:

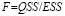(8)

где

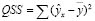(9)

– факторная дисперсия.

Для оценки величины F-критерия Фишера также можно применить следующую формулу:

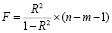, (10)

где n – длина временного ряда результативного признака, отражающая количество исследуемых наблюдений,

m – количество факторных признаков, включенных в уравнение регрессии.

Полученное расчетным путем значение F-критерия Фишера соотносят с его критическим значением, при этом необходимо учесть заданный уровень значимости α(0,05 или 0,01) и число свободы 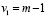, 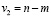. Если Fфакт > Fтабл , то полученное уравнение регрессии признается статистически значимым, в противном случае уравнение регрессии признается статистически не значимым, и необходимо пересмотреть набор факторов-регрессоров [5].

Третьим направлением в оценке качества регрессионного уравнения является оценка статистической значимости факторов-регрессоров, которая может быть выполнена с использованием t-критерия Стьюдента по следующей формуле:

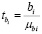, (11)

где bi – коэффициенты регрессии при факторных признаках;

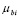– величина стандартной ошибки коэффициента регрессии при соответствующем факторе-регрессоре.

Расчетное значение t-критерия Стьюдента сравнивается с критическим значением критерия, определенным с учетом степеней свободы n-m и заданной вероятности расчетов α (0,01; 0,05). Если расчетное значение t-критерия превышает критическое, то делается вывод о статистической значимости соответствующего параметра регрессии и статистической значимости фактора-регрессора и правомерности его включения в регрессионное уравнение [6].

Данный математический аппарат реализован в среде SPSS Statistics, которая была использована при анализе уровня социально-экономического развития Смоленской области в динамике за 2010–2022 годы. В качестве результативного признака Y(t) по усмотрению исследователей был выбран показатель «валовой региональный продукт на душу населения», характеризующий уровень развития региона в целом. В качестве факторов-регрессоров по усмотрению исследователей выбраны следующие экзогенные переменные: стоимость основных фондов (Х1, млн руб.), численность населения региона (Х2, тысяч), численность занятого населения (Х3, тысяч), средняя заработная плата по региону (Х4, тыс. руб.), инвестиции в основные фонды (Х5, млн руб.).

Для выявления корреляционной зависимости обозначенной системы показателей была использована функция «Корреляция» SPSS Statistics. Фрагмент реализации данной операции представлен следующим образом:

GET DATA

/TYPE=XLSX

/FILE=’C:\Users\Desktop\!2024\Стат данные.xlsx’

/SHEET=name ‘Лист1’

/CELLRANGE=FULL

/READNAMES=ON

/DATATYPEMIN PERCENTAGE=95.0

/HIDDEN IGNORE=YES.

EXECUTE.

DATASET NAME Наборданных2 WINDOW=FRONT.

CORRELATIONS

/VARIABLES=YВРП X1СОС X2ЧН X3ЧЗН X4СЗП X5ИОС

/PRINT=TWOTAIL NOSIG

/MISSING=PAIRWISE.

Фрагмент полученной матрицы корреляционных зависимостей выбранной системы показателей представлен в таблице 1.

Таблица 1

Итоги расчетов корреляционных зависимостей системы показателей

Источник: составлено авторами по [7].

** – коэффициент корреляции признается значимым.

Таблица 2

Результаты построения многофакторной регрессии в SPSS Statistics

Источник: составлено авторами

По результатам расчетов можно утверждать, что все выбранные факторы-регрессоры имеют достаточно сильную корреляционную связь с результативным признаком, что подтверждается значением коэффициентов корреляционной связи в интервале (0,814–0,995). Следует отметить, что фактор-регрессор Х4 (средняя заработная плата по региону) по усмотрению исследователей, исходя из экономического смысла, из рассмотрения был исключен. С факторами-регрессорами Х2, Х3 (численность населения региона и численность занятого населения) наблюдается тесная отрицательная связь результативного признака Y (ВРП на душу населения), что свидетельствует об ориентированности экономики региона на интенсивный путь развития, связанный с внедрением инноваций и современных технологий. Показатели Х1 (стоимость основных фондов) и Х5 (инвестиции в основные фонды) имеют устойчивую положительную корреляцию с эндогенной переменной Y (величина ВРП на душу населения). Результаты регрессионной статистики по итогам построения многофакторной модели представлены в таблице 2.

На основании полученных результатов можно записать уравнение множественной регрессии:

Y = 3891,711 – 0,001*Х1 –

– 4,162*Х2+0,721*Х3 + 0,001*Х5 , (12)

которое по F-критерию Фишера, равному 267,9, признается статистически значимым и имеет высокое качество, что подтверждают такие характеристики, как коэффициент детерминации R-квадрат = 0,993, значение которого достаточно близко к 1, и достаточно высокое значение коэффициента R = 0,996 множественной корреляции, характеризующее тесноту связи факторов-регрессоров и эндогенной переменной.

В дополнение к данной модели множественной регрессии, исходя из целей и задачи исследования, могут быть построены следующие модели: многофакторная регрессия только со статистически значимыми факторами-регрессорами, модели парной регрессии от каждого из рассмотренных факторов, что позволит осуществить проведение более детального исследования каждой переменной, входящей в систему рассматриваемых показателей. В дополнение к этому может быть осуществлен трендовый анализ факторов-регрессоров, что позволит в автоматическом режиме в среде SPSS Statistics построить прогнозы по исследуемым показателям и таким способом определить прогнозные значения эндогенной переменной, формируемой под воздействием факторов-регрессоров. По усмотрению исследователей может быть определен другой набор экзогенных переменных для получения различных вариантов регрессионных моделей и повышения достоверности результатов. Выбор лучшей по качеству модели должен осуществляться на основании экономико-статистического анализа рассматриваемой системы показателей, но обязательно с учетом математических методов оценки качества регрессий.

Заключение

Рассмотренные методологические аспекты и методика оценки качества математических моделей актуальны и могут быть использованы для решения широкого круга прикладных задач, в том числе для моделирования и исследования динамики показателей, характеризующих уровень социально-экономического развития региональных субъектов.

Практическая значимость исследования заключается в том, что инвариантные многофакторные регрессионные модели могут быть применены для определения перспективных значений ряда показателей регионов, что актуально при разработке стратегий развития региональных субъектов на краткосрочную и долгосрочную перспективу с использованием математического моделирования и инструментария корреляционно-регрессионного анализа. Использование для построения математических моделей и проведения дальнейшего анализа среды SPSS Statistics, позволяющей автоматизировать большую часть статистических расчетов, отражает общую тенденцию расширения сфер применения цифровых технологий в научных исследованиях и практической деятельности.

Библиографическая ссылка