Современные вызовы в производственной сфере летательных аппаратов требуют разработки и внедрения новых производственных и технологических процессов, интенсификации работы существующих, что возможно осуществить за счет разработки новых, современных, точных и надежных методов моделирования технологических процессов, на основе математических моделей способных обеспечить требуемую точность [1–3]. Это играет ключевую роль в производстве многослойных композиционных конструкций методом полимеризации для летательных аппаратов [4–6]. Существенной особенностью таких технологических процессов является то, что они производятся в пресс-формах или автоклавах. Поэтому описывать возникающие температурные поля приходится с учетом формы изделия в прямоугольно-декартовой, цилиндрической или сферической системах координат [7, с. 16; 8]. Решение задач с неоднородными граничными условиями возможно стандартными методами, но в результате получаются трудно-сходящиеся ряды. Поэтому решение задачи теплопроводности наиболее целесообразно и оптимально производить за счет выделения стационарной составляющей температурного поля. В результате улучшается сходимость рядов, значительно снижается число вычислений, а также возникающая вычислительная погрешность [6; 9]. Таким образом, для получения решения задач теплопроводности в многослойных изделиях, имеющих неоднородные граничные условия, воспользуемся алгебраической суммой, которая включает решения стационарной задачи теплопроводности с неоднородными граничными условиями и нестационарной задачи теплопроводности с однородными граничными условиями [6]. Поставленную задачу решим методом конечных интегральных преобразований [10].
Цель исследования – создать математические модели теплообмена в многослойной пластине в прямоугольно-декартовой системе координат, в неограниченном сплошном и полом многослойном цилиндре, в сплошном и полом многослойном шаре в соответствующих системах координат, которые служат основой для разработки автоматизированных систем управления описанных процессов.
Материалы и методы исследования
В работе применим аналитические методы, которые позволяют учитывать влияние теплофизических параметров на производственные процессы многослойных композиционных конструкций. Рассмотрим температурные поля в многослойной пластине в прямоугольно-декартовой системе координат, в неограниченном сплошном и полом многослойном цилиндре, в сплошном и полом многослойном шаре в соответствующих системах координат при производстве композитов [6]. Например, если рассматриваемая конструкция имеет форму полого цилиндра, то необходимо проводить исследование в цилиндрической системе на конечно-разностном аналоге (рисунок).
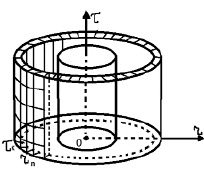
Полый цилиндр
Для трех систем координат задача, в которой имеются произвольные начальные условия, неоднородные граничные условия и распределенный внутренний источник тепла, представляется следующим образом:
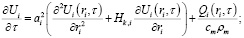(1)
i=1,2,…,N; Ri-1 ≤ ri ≤ Ri ; k = 0,1,2; τ > 0,
с начальными условиями
Ui (ri ,0) = fi(ri); (2)
с неоднородными граничными условиями
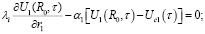(3)
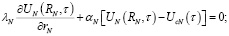(4)
условия сопряжения
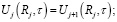
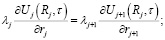j = 1,2,…,N–1. (5)
Здесь: Ui(ri,τ) – i-й области температурное поле; ri – координата в пространстве; τ – временной параметр; аi2 – коэффициент температуропроводности i-го слоя; Hk,i – коэффициент уравнения, который определяется за счет вида координат (декартовая система координат имеет значение равное k = 0, H0,i = 0; цилиндрическая система k = 1, H1,i = 1/ri; сферическая система k = 2, H2,i = 2/ri); Qi(ri,τ) – коэффициент, связанный с мощностью внутреннего источника тепла i-й области; cm – коэффициент удельной теплоемкости слоя; ρm – плотность слоя; N – общее количество слоев; Ri – толщина i-й пластины; Uc1, UcN – температуры окружающей среды как функции времени; αi – коэффициент, связанный с конвективной теплоотдачей от внешней поверхности в окружающую среду; λi – теплопроводность i-го слоя.
Решение поставленных задач основывается на конечном интегральном преобразовании
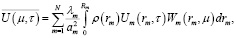(6)
где μ – параметр; Wm(rm,μ) – ядро интегрального преобразования; ρ(rm) – весовая функция каждого слоя, которая является решением уравнения следующего вида
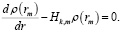(7)
В декартовой системе координат весовая функция равна ρ(rm) = 1; в цилиндрической соответственно ρ(rm) = rm; в сферической ρ(rm) = rm2.
Входящее в уравнение (6) ядро Wm(rm,μ) является решением задачи Штурма – Лиувилля:
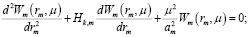i=1,2,…,N; Rm-1 ≤ rm ≤ mi; (8)
однородные граничные условия
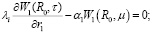(9)
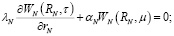(10)
и условия сопряжения
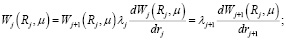j =1,2,…,N. (11)
Решением уравнения (8) является
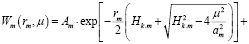
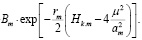(12)
При этом в зависимости от применяемой системы координат меняется вид:
в декартовой
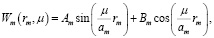(13)
в цилиндрической
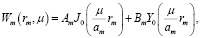(14)
в сферической
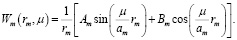(15)
Для определения коэффициентов Am и Bm используем граничные условия (9)–(11), а также параметр μ, а также А1 = 1, и функции J0(z), Y0(z) – функции Бесселя первого рода нулевого порядка и второго рода нулевого порядка.
Для перехода к изображениям необходимо уравнение (6) применить почленно к уравнениям (1) и (2). Интегралы в правой части уравнения (6) берутся по частям, при этом необходимо учитывать граничные условия (3)–(5) и (9)–(11). В изображениях частой производной по времени получим
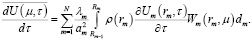(16)
Изображения по координатам принимают следующий вид
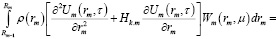
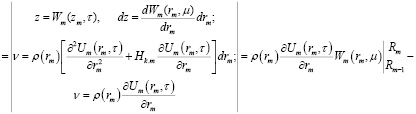
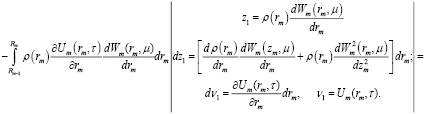
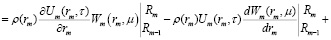
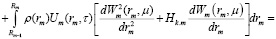
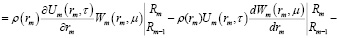
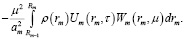(17)
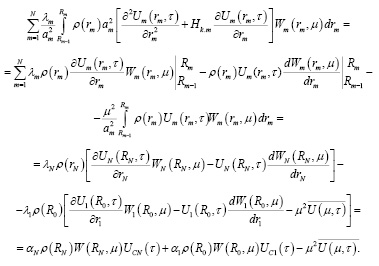(18)
Изображение начального условия имеет вид
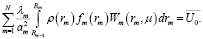(19)
Изображение функции источника имеет вид
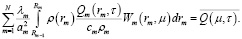(20)
Таким образом, исходная задача в изображениях имеет вид
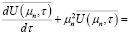
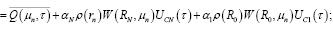(21)
с начальным условием
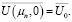(22)
Решая задачи (21)–(22), в изображениях получим
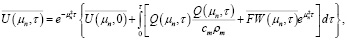(23)
где 
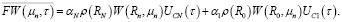(24)
К оригиналу переходят по формуле
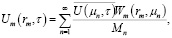(25)
где
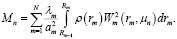(26)
Результаты исследования и их обсуждение
В результате такого подхода к решению нелинейных задач нестационарной теплопроводности с нелинейными граничными условиями и функциями источника, получают аналитические решения, содержащие сходящиеся ряды.
Заключение
Таким образом, следует отметить, что разработаны математические модели теплообмена в многослойной пластине в прямоугольно-декартовой системе координат, в неограниченном сплошном и полом многослойном цилиндре, в сплошном и полом многослойном шаре в соответствующих системах координат при производстве композитов. Используя аналитические решения представленных задач, возможно произвести оценку распределения температуры со временем в каждом слое изделия и получить сходящиеся ряды. Разработанная теория позволяет построить математические модели целого класса технологических процессов производства многослойных композиционных конструкций, которые служат основой для разработки автоматизированных систем управления описанных процессов. Для повышения качества и расширения видов производимых изделий необходимо провести дополнительные исследования ограждающих конструкций.
Библиографическая ссылка
Тугов В.В. МОДЕЛИРОВАНИЕ И РЕШЕНИЕ НЕЛИНЕЙНЫХ ЗАДАЧ НЕСТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ В МНОГОСЛОЙНЫХ КОНСТРУКЦИЯХ // Современные наукоемкие технологии. – 2024. – № 5-1. – С. 76-81;URL: https://top-technologies.ru/ru/article/view?id=40008 (дата обращения: 17.07.2024).