Задачи эффективного использования информационных ресурсов, их оптимальная загрузка, сокращение времени вычисления и возможность гарантированного обеспечения требуемого качество сервиса (SLA) являются ключевыми для распределенной вычислительной среды центра обработки данных (ЦОД) облачных сред. Как показали многочисленные исследования, между подсистемами ЦОД передаются информационные потоки телекоммуникационного трафика, характеризуемого хаотической структурой, самоподобием, долговременной зависимостью. Широко известные алгоритмы балансировки нагрузки используют приближенные линейные или эвристические подходы, которые не учитывают особенности фрактальной структуры нагрузки современных мультисервисных сетей и не обеспечивают статистически равномерную загрузку серверов кластеров ЦОД. Возможным подходом к решению данных задач является использование методов нелинейной динамики, учитывающих статистическое самоподобие нагрузки и обеспечивающих решение задачи прогнозирования моментов предполагаемых всплесков нагрузки, используемых для своевременного выделения необходимых ресурсов для ее обработки. В нелинейной динамике подобные системы исследуются методом реконструкции фазового пространства по набору значений одномерного временного ряда, являющегося отражением ее состояния. Данный подход дает возможность определять свойства нелинейного процесса по отдельным элементам описывающего его временного ряда, является основой построения прогнозной модели и динамического распределения нагрузки ЦОД в условиях фрактальной сетевой нагрузки.
Материалы и методы исследования
Одним из направлений решения задачи рационального использования аппаратно-программных ресурсов ЦОД в условиях неоднородной нагрузки является ее статистически равномерное распределение в среде серверов ЦОД. Фрагмент рассматриваемой системы представлен на рис. 1 и используется как основа построения ЦОД облачных сред. Обеспечить своевременное выделение необходимых ресурсов ЦОД можно путем прогнозирования предполагаемых всплесков нагрузки и рационального ее распределения по серверам кластеров. Задача прогнозирования решается методом реконструкции фазового пространства нелинейной системы по порожденному временному ряду динамики ее развития, основанному на поиске и выделении k ближайших фазовых траекторий и последующем восстановлении фазового пространства [1–3]. При этом распределение нагрузки осуществляется с использованием известных алгоритмов балансировки RR, WRR, CAP, LARD, AMLB, TLоB с добавлением элементов прогнозных решений.
Распределитель нагрузки, построенный на базе программируемого контроллера [4], реализует динамический алгоритм балансировки нагрузки, характеризуемой специальными свойствами второго порядка, самоподобием, последействием, осуществляя при этом прогнозные оценки интенсивности входящего потока запросов, а также фильтрацию, исключение аномальных отсчетов, сглаживание данных, например, с помощью методов сингулярного спектрального анализа. Критерий оценки эффективности алгоритма основан на показателях загрузки серверов кластеров ЦОД, при условии минимального отклонения их загруженности от заданного значения.
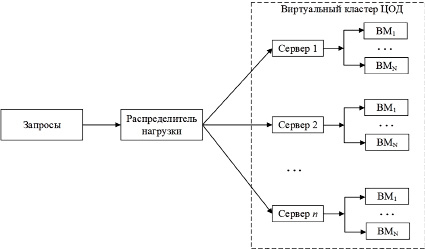
Рис. 1. Структурная схема фрагмента ЦОД
Модель балансировки нагрузки в кластере ЦОД имеет вид
,
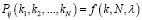где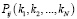 
– матрица распределения i-х запросов по 
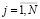серверам кластера;
N – число серверов;
λ – интенсивность входящего потока запросов.
При реализации алгоритма прогнозирования данное выражение будет иметь вид
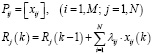
где xij – матрица распределения ресурсов;
λij(k)– прогноз интенсивности нагрузки на k-м шаге.
При этом отклонение по нагрузке каждого из серверов должно быть минимальным
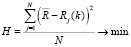
при условии
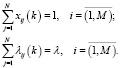
Прогнозная модель представляется в виде
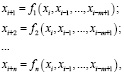
где xi – элементы числового ряда;
m – размерность фазового пространства;
;
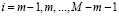fn – нелинейный полином
,
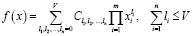где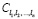 
– коэффициенты V-го полинома;
m – размерность фазового пространства;
ln – числовые значения полинома.
Время упреждения прогноза T = m∙τ, где τ – временная задержка.
В [5] представлен алгоритм построения реконструированного аттрактора динамической системы.
Временная задержка τ определяется из условия равенства нулю автокорреляционной функции B(τ)
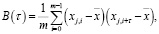
m = M – τ,
где xj – фазовая координата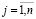 
;
m – размерность фазового пространства;
xji – одномерная реализация временного ряда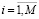 
.
Другой подход определения τ предполагает использование метода средней взаимной информации и функции
,
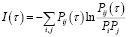где Pji(τ) – совместная вероятность нахождения точек Pi и Pj(τ) аттрактора. Пример зависимости I(τ) от τ приведен на рис. 2. Значение τ определяется по первому минимуму функции I(τ).
Размерность вложения m вычисляется на основании свойств корреляционного интеграла C(e)
,
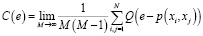где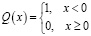 
;
;
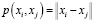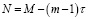– количество точек аттрактора;
e – радиус окружности вокруг точек аттрактора.
При этом необходимо исключить точки числового ряда, расположенные на расстоянии меньше ω (окно Тейлора)
.
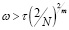Числовое значение m определяется по тангенсу угла наклона графика зависимости logC(e) от log(e).
В основе другого подхода вычисления размерности m, допускающего его простую программную реализацию, лежит теорема о вложении, определяющая, что в восстанавливаемой системе должны быть исключены самопересекающиеся фазовые траектории и все точки фазового пространства должны пересекаться только одной траекторией.
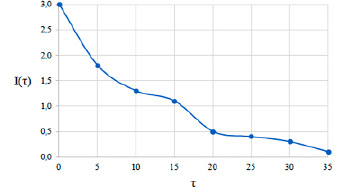
Рис. 2. Зависимость по времени функции I(τ)
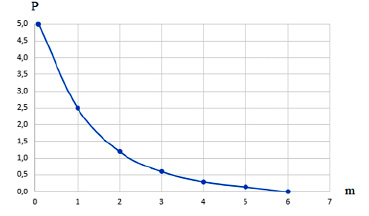
Рис. 3. Зависимость P от m
При таком подходе необходимо многократно вычислять расстояние между точками временного ряда в реконструируемом фазовом пространстве
,
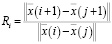увеличивая на каждом шаге значение m и определяя количество ближайших соседей P. При P/N = 0 получаем оптимальное значение m. Пример зависимости количества ближайших соседей P от размерности вложения m приведен на рис. 3.
Проверка на хаотичность временного ряда осуществляется с помощью показателя Ляпунова λ1, положительное значение которого определяет хаотическое поведение процесса. Максимальный показатель Ляпунова характеризует скорость расхождения фазовых траекторий и определяется выражением [6]
,
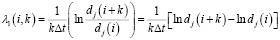где Δt – период ряда; dj(i) – расстояние между близкими соседями,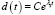 
, 
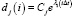– скорость расхождения близких траекторий.
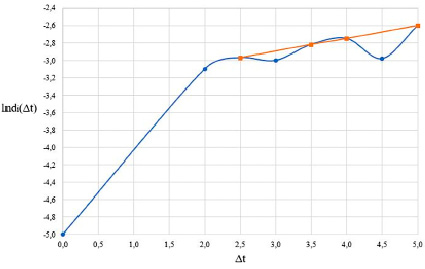
Рис. 4. График определения λ1
Отсюда следует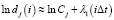 
, то есть λ1 определяется как тангенс угла наклона прямой, аппроксимирующей данную зависимость. С использованием программ пакета TISEAN 3.0.1 определены значения спектра показателей Ляпунова.
На рис. 4 приведен пример графика расхождения траектории аттрактора и его аппроксимирующая прямая.
Для повышения точности прогноза необходимо реализовать алгоритм устранения случайных шумовых компонент входного телекоммуникационного трафика. Выделить наиболее информативные компоненты временного ряда, порождаемого сетевым трафиком, устранить шумы и случайные возмущения предлагается с помощью метода сингулярного спектрального анализа (SSA) [7, 8]. Метод реализуетпроцедуру декомпозиции скалярного временного ряда {x1, x2,…,xN} и получение K = N – L + 1 векторов вложения, 1 < L < N, где N – длина временного ряда. Из полученных векторов вложения составляется траекторная матрица X. Для матрицы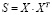 
получаем N собственных чисел 
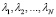и N ортонормированных собственных векторов
, 
.
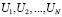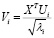Выражение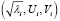 
является i-й собственной тройкой сингулярного разложения, а выражение (
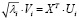) – вектором i-й главной компоненты. Уровень наиболее значимых составляющих временного ряда зависит от параметров собственных троек сингулярного разложения. При исследовании системы, построения и управления матрицами и векторами алгоритма SSA используются программные пакеты линейной алгебры Maple, linalg, LinalgAlgebra, MTT. Пример численных значений главных компонент временного ряда приведен на рис. 5.
Очевидно, что первые три компоненты практически полностью определяют поведение ряда. Дальнейшая группировка собственных троек и диагональное усреднение результирующей матрицы обеспечивают разложение исходного ряда на сумму восстановленного ряда и шума.
При этом доля самого незначительного вклада в общую дисперсию данных приходится на шумовые компоненты [9]. SVD-разложение представляется в виде
, 
,
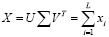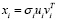где ∑ – диагональная матрица, xi – элементарная матрица.
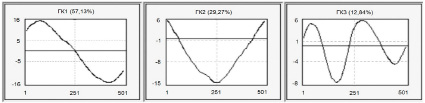
Рис. 5. Главные компоненты временного ряда
Сингулярный спектр определяется выражением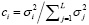 
.
На этапе восстановления L матриц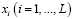 
делится на τ непересекающихся групп, а матрица X переходит в матрицу 
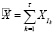, где 
.
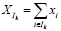Диагональное усреднение матриц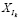 
обеспечивает преобразование ряда SN в ряд 
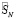с элементами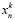 
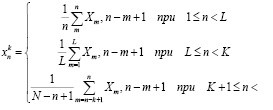
и, следовательно, исходный временной ряд раскладывается на сумму восстановленного ряда и выделенного шума
.
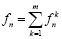Показателем качества, определяющим долю не устраненных шумовых компонент, является выражение [10]
,
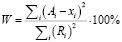где Ai – элементы восстановленного ряда,
Ri – элементы шума.
Динамический алгоритм балансировки нагрузки, построенный на основе локального метода ее прогнозирования, представлен ниже и включает в себя следующие шаги:
1. Оценка требуемого количества элементов ряда Nmin , проверка его на хаотичность по старшему показателю Ляпунова
,
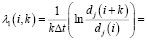
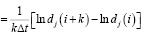λ1 > 0 – хаотическое движение, λ1 ≤ 0 – регулярное движение. Реализация фильтрующего алгоритма с использованием метода SSA.
2. Реконструкция фазового пространства с определением лага τ с помощью метода средней взаимной информации и функции
,
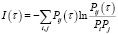а также вычисление размерности вложения m с использованием корреляционного интеграла C(e)
.
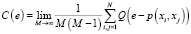3. Разработка прогнозной модели на базе алгебраического полинома степени V одинакового для всех его переменных
.
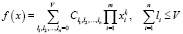4. Прогнозная оценка интенсивности нагрузки на k-м шаге λij(k).
5. Распределение запросов по серверам
.
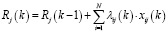Результаты исследования и их обсуждение
В настоящее время для решения задач управления нагрузкой ЦОД широко применяются методы математической статистики. Данные методы не учитывают хаотическую структуру нагрузки, характеризующуюся нелинейным характером и фрактальным самоподобием. Большое количество публикаций посвящено также исследованию поведения детерминированных динамических систем методами нелинейного анализа и теории хаоса. Однако подобные работы практически не содержат реализуемые методики решения нелинейных прикладных задач. Решить некоторые из них, получить численные результаты исследований и стало одной из целей данной работы. Возможным подходом к решению данных задач является использование алгоритмов прогнозирования, разработанных на основе методов нелинейной экстраполяции состояний сетевого трафика, размерность фазового пространства которого неизвестна. Восстановление фазового пространства процесса методами нелинейной динамики дает возможность определять его свойства по отдельным параметрам описывающего его временного ряда, является основой построения прогнозной модели и динамического распределения нагрузки ЦОД.
Заключение
В настоящей работе сформулирована и решена задача распределения и балансировки нагрузки ЦОД, отличающаяся применением механизма прогнозирования состояний сетевого трафика, характеризуемого фрактальным самоподобием. В основу решения задачи положены особенности фрактального сетевого трафика, отражающие характер изменения информационной нагрузки ЦОД. Реконструкция фазового пространства подобного динамического процесса осуществлена в соответствии с теоремой Такенса – Мане, с использованием метода задержек. Разработаны математическая модель и динамический алгоритм прогнозной модели состояния нелинейной системы. Прогнозная модель представлена в виде системы дискретных отображений предыдущих и последующих значений временного ряда и связующих их аппроксимирующего полинома степени v. При этом горизонт прогноза меняется в соответствии с изменением интенсивности входящей нагрузки. Проверка на хаотичность временного ряда осуществляется путем определения значений спектра показателей Ляпунова с использованием программ пакета TISEAN 3.0.1. Алгоритм фильтрации шумов входного телекоммуникационного трафика реализован методом сингулярного спектрального анализа (SSA). Разработанный динамический алгоритм распределения и балансировки нагрузки обеспечивает выбор рациональных параметров балансировки по критерию равномерной загрузки ресурсов серверов.
Библиографическая ссылка
Мочалов В.П., Братченко Н.Ю., Гостева Д.В. АЛГОРИТМ БАЛАНСИРОВКИ НАГРУЗКИ ЦЕНТРА ОБРАБОТКИ ДАННЫХ НА ОСНОВЕ НЕЛИНЕЙНОЙ ПРОГНОЗНОЙ МОДЕЛИ // Современные наукоемкие технологии. – 2024. – № 3. – С. 62-68;URL: https://top-technologies.ru/ru/article/view?id=39947 (дата обращения: 23.11.2024).