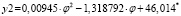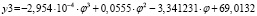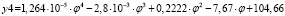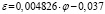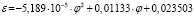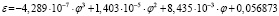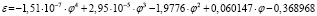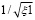Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Середа С.Н. 1

---

1 Муромский институт (филиал) ФГБОУ ВО «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых»

Целью работы является поиск функции аппроксимации коэффициента местного сопротивления воздушной заслонки в системе вентиляции и оценка его влияния на воздухообмен вентилируемого помещения посредством компьютерного моделирования. В работе проводится определение коэффициентов полиномиальной регрессии различного порядка как функции аппроксимации местного сопротивления воздушной заслонки методом наименьших квадратов, отмечаются проблемы применения данного подхода при решении задачи расчета динамики расхода воздуха. Рассматривается нелинейная функция аппроксимации местного сопротивления и его обратной зависимости, а оценка параметров функции проводится методом линеаризации. Предложена параметрическая модель функции аппроксимации на основе логистической функции, оптимальные значения параметров которой находятся алгоритмически по критерию минимума среднеквадратического отклонения. Рассмотренные варианты функций аппроксимации можно использовать при расчете воздухообмена в системе с автоматическим регулированием угла раскрыва воздушной заслонки. Построена математическая модель динамики воздушного режима в виде системы дифференциальных уравнений. Приводится пример моделирования воздушного режима вентилируемого помещения при линейном изменении угла раскрыва воздушной заслонки в программе MathCAD итерационным методом Рунге – Кутты с учетом предложенной модели функции аппроксимации. Результаты моделирования могут быть использованы при проектировании и настройке регулируемых параметров систем вентиляции.

Статья в формате PDF

1492 KB

вентиляция

воздухообмен

математическое моделирование

микроклимат

регрессия

функция аппроксимации

1. ГОСТ 30494-2011. Здания жилые и общественные. Параметры микроклимата в помещениях. М.: Стандартинформ, 2013. 12 с.

2. СанПиН 1.2.3685-21 Гигиенические нормативы и требования к обеспечению безопасности и (или) безвредности для человека фактов среды обитания. Дата введения 2021-03-01, 2021. 469 с.

3. СП 60.13330.2020. Отопление, вентиляция и кондиционирование. Актуализированная редакция СНиП 41-01-2003. Дата введения 2021-07-01. М.: Стандартинформ, 2021. 149 с.

4. Внутренние санитарно-технические устройства. В 3 ч. Ч. З. Вентиляция и кондиционирование воздуха / В.Н. Богословский, А.И. Пирумов, В.Н. Посохин и др.; Под ред. Н.Н. Павлова и Ю.И. Шиллера. М.: Стройиздат, 1992. 319 с.

5. Большаков А.А., Каримов Р.Н. Методы обработки многомерных данных и временных рядов: учеб. пособие для вузов. М.: Горячая линия – Телеком, 2007. 522 с.

6. Середа С.Н. К вопросу аппроксимации эмпирических зависимостей // Международный научно-исследовательский журнал. 2017. Т. 5, № 12 (66). С. 133–136.

7. Karl-Georg Steffens. The History of Approximation Theory. From Euler to Bernstein. Boston: Birkhauser, 2006. 235 p.

8. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы. СПб.: Лань, 2023. 672 с.

9. Горлач Б.А. Теория вероятностей и математическая статистика: учебно-методическое пособие. СПб.: Лань, 2022. 320 с.

Системы вентиляции и кондиционирования воздуха жилых помещений, равно как и производственных помещений, предназначены для формирования микроклимата с целью обеспечения безопасных и комфортных условий жизнедеятельности человека, которые должны соответствовать требованиям ГОСТ и санитарно-эпидемиологических норм [1, 2]. При проектировании систем внутреннего тепло- и холодоснабжения, вентиляции и кондиционирования воздуха в общественных и жилых зданиях нужно соблюдать требования энергоэффективности, а также применять передовые технологии, в том числе интеллектуальные системы автоматического управления климатическими системами здания [3]. При расчете требуемого воздухообмена зданий учитываются конструктивные характеристики вентиляторов, воздуховодов, воздушных дефлекторов, задвижек и других элементов системы вентиляции [4].

Для эффективного управления режимом работы систем вентиляции в алгоритме блока автоматического регулирования необходимо обеспечить плавное изменение регулируемого параметра по заданному закону. В качестве регулируемого параметра может выступать угол раскрыва воздушной заслонки в системе вентиляции. При использовании табличных данных, а также при обработке результатов эксперимента возникает задача аппроксимации зависимостей некоторой аналитической функцией, для решения которой могут применяться различные методы [5–7], как то: кусочно-линейная аппроксимация, аппроксимация тригонометрическими функциями, полиномами Чебышева, сплайны и др., в некоторых случаях не удается с помощью таких подходов получить приемлемо хорошее приближение, либо аналитическая функция не позволяет получить общую математическую модель исследуемого процесса, как, например, при использовании сплайнов. Целью данной работы является поиск функции наилучшего приближения зависимости коэффициента местного сопротивления воздушной заслонки от угла раскрыва для расчета аэродинамического режима помещения.

В качестве исходных данных для исследования выступают значения коэффициента местного сопротивления воздушной заслонки ξ при изменении угла открытия φ (табл. 1), представленные в справочнике проектировщика систем вентиляции [4, с. 133]. При этом зависимость ξ(φ) носит нелинейный характер.

Таблица 1

Исходные данные

С учетом этого можно рассчитать расход воздуха Gв (кг/с) через воздуховод с регулируемой воздушной заслонкой или через ветровой проем помещения по формуле

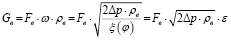, (1)

где Fв – площадь сечения воздуховода, м2; Δp – потери давления через заслонку (проем), Па; ω – скорость движения воздуха, м/с; ρв – плотность воздуха, кг/м3; ξ – коэффициент местного сопротивления проема, зависящий от угла раствора φ.

В случае автоматического регулирования угла раскрыва заслонки с непрерывным шагом необходимо вычислять значения коэффициента местного сопротивления по некоторой формуле. Также эта проблема возникает при решении задачи расчета динамики изменения параметров микроклимата вентилируемых помещений в нестационарном режиме итерационными методами. Следовательно, научно-практический интерес представляет задача аппроксимации таблично заданной зависимости некоторой аналитической функцией, удобной для последующего применения.

Материалы и методы исследования

Рассмотрим задачу поиска функции аппроксимации с помощью полиномиальной регрессии. Уравнение регрессии n-го порядка имеет вид

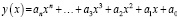, (2)

где 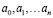– коэффициенты полинома регрессии.

Для нахождения значений коэффициентов регрессии n-го порядка воспользуемся методом наименьших квадратов [8]. Для этого необходимо решить систему нормальных уравнений:

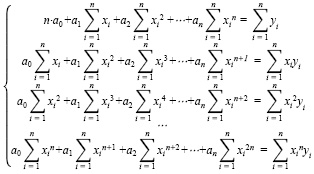(3)

или в матричной форме записи

X ∙ A = Y, (4)

где A – вектор искомых коэффициентов полинома регрессии; X – матрица, составленная по данным аргумента функции xi; Y – вектор, составленный по правым частям уравнений (3).

Тогда значения вектора коэффициентов полинома регрессии можно найти по формуле

A = X –1 ∙ Y, (5)

где X–1 – обратная матрица.

Как критерий качества аппроксимации, показывающего меру близости результатов, полученных расчетным путем, и табличных данных, используем минимум среднеквадратического отклонения (СКО) и коэффициент корреляции Пирсона r [9].

В табл. 2 приведены результаты расчета функции регрессии местного сопротивления, а на рис. 1 – графики функций регрессии, полученные в программе MathCAD.

По результатам расчета можно сделать вывод, что ни одна из функций регрессии не обеспечивает качество аппроксимации, а именно, при малых порядках регрессии получаем значительные ошибки аппроксимации, а при порядке регрессии n = 4, несмотря на точное совпадение расчетных и табличных данных, функция аппроксимации принимает отрицательные значения в интервале 69° < φ < 88°, которые нельзя компенсировать как в случае регрессии второго порядка, также имеющей провал при 63° < φ < 76°, без существенной потери точности. Функция регрессии третьего порядка имеет подъем на интервале 50° ≤ φ ≤ 80°, что противоречит характеру изменения местного сопротивления. Отрицательные или нулевые значения функции при расчете воздухообмена по формуле (1) приводят к вычислительным ошибкам деления на ноль или комплексным величинам. Возможно избежать подобных коллизий, если искать функцию аппроксимации для со-зависимой величины ε = 1/ξ или 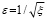, входящей в уравнение (1), используя метод линеаризации. В этом случае в уравнении (3) параметр yi соответствует обратным величинам 1/ξi или .

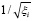Таблица 2

Функции полиномиальной регрессии коэффициента местного сопротивления

Примечание. *Коэффициент a0 = 46,014 в уравнении регрессии второго порядка приводится с учетом поправки +0,316 для исключения отрицательных значений функции (при 63° < φ < 76°).

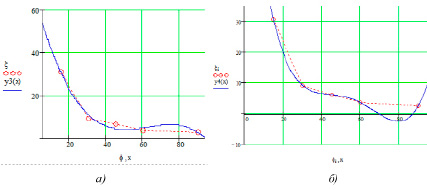
Рис. 1. Графики функций регрессии местного сопротивления а) n = 3; б) n = 4

Таблица 3

Функции регрессии обратных зависимостей местного сопротивления

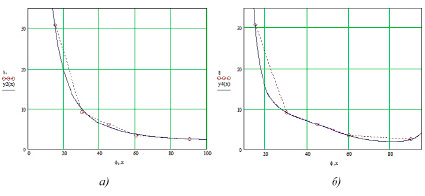
Рис. 2. Графики функций регрессии местного сопротивления а) n = 2; б) n = 4

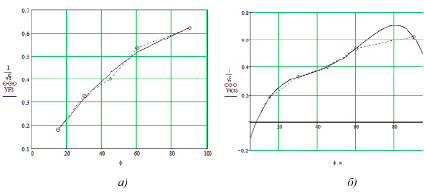
Рис. 3. График функций регрессии коэффициента местного сопротивления, а) n = 2; б) n = 4

В табл. 3 приведены результаты расчета функции регрессии местного сопротивления, вычисленного как обратная величина от функции регрессии, а на рис. 2 – графики функций регрессии, полученные в программе MathCAD.

Как видно из рис. 2, найденные функции регрессии 2-го и 3-го порядка являются монотонными убывающими. При этом функция регрессии 2-го порядка дает даже меньшую ошибку аппроксимации местного сопротивления, а в сравнении с функцией ε ошибка СКО равна 7 ∙ 10–3, что говорит о хорошем качестве аппроксимации (рис. 3, а).

Функция регрессии 4-го порядка при точном совпадении с табличными данными имеет два существенных недостатка: функция равна 0 при φ = 8 (что приводит к ξ = ∞), а при φ > 80 величина, обратная коэффициенту местного сопротивления ξ, убывает (рис. 3, б).

Если в качестве функции аппроксимации выбрать зависимость обратной величины коэффициента местного сопротивления, то с учетом найденных значений коэффициентов регрессии (табл. 3), при расчете воздухообмена по формуле (1), будем определять величину 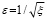по формуле

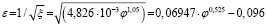. (6)

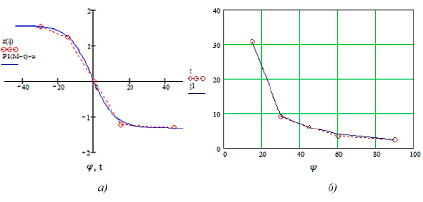
Рис. 4. Графики функций аппроксимации коэффициента местного сопротивления

Таблица 4

Логистическая функция аппроксимации местного сопротивления

При этом график зависимости аналогичен показанному на рис. 3, а (СКО равно 0,754), однако начальное значение –0,096 приводит к ошибке деления на ноль при значении угла φ ≈ 1,85°.

Рассмотрим центрированную функцию от коэффициента местного сопротивления вида

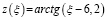. (7)

Тогда в качестве функции аппроксимации зависимости (7) можно использовать модифицированное логистическое уравнение Ферхюльста:

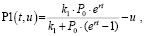(8)

где k1, k2, r, P0, u, t, M – параметры модели, причем 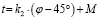; φ – угол раскрыва, град.

Модель (8) является параметрической, и поиск значений параметров модели рассматривается как алгоритмическая задача оптимизации по критерию наилучшего приближения СКО. Тогда значения коэффициента местного сопротивления можно вычислить по формуле

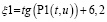. (9)

На рис. 4 приведены зависимости z(ξ) и функции аппроксимации (8) (рис. 4, а), а также расчетные значения коэффициента местного сопротивления по формуле (9) (рис. 4, б) при следующих значениях параметров: k1 = 2,871, k2 = –0,2, r = 0,794, P0 = 1,575, u = 1,311, M = –0,508 найденных алгоритмом поиска на языке программирования Python.

В табл. 4 приведены результаты расчета функции аппроксимации местного сопротивления по формуле (9), а также обратные величины 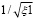для дальнейшего расчета по формуле (1). Полученные результаты показывают высокую точность приближения к исходным данным.

Результаты исследования и их обсуждение

Динамику изменения расхода воздуха в системе вентиляции при линейном изменении угла раскрыва воздушной заслонки, в случае аппроксимации коэффициента местного сопротивления функцией регрессии второго порядка (2) (табл. 3), можно описать системой дифференциальных уравнений:

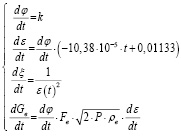,(10)

где k – угловой коэффициент, определяющий линейную скорость изменения угла раскрыва воздушной заслонки (в модели k = 9 при полном раскрытии заслонки за время t = 10 с).

Для решения системы уравнений была использована встроенная функция rkfixed в программе Mathcad, реализующая итерационный метод Рунге – Кутты. Результаты компьютерного моделирования динамики воздухообмена приведены на рис. 5.

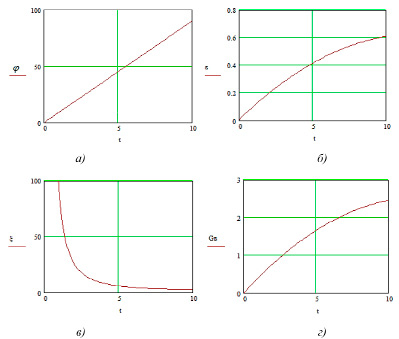
Рис. 5. Модель динамики воздухообмена: а) угол раскрыва заслонки; б) коэффициент 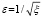; в) коэффициент местного сопротивления ξ; д) расход воздуха, кг/с

Как видно из модельных результатов, коэффициент местного сопротивления уменьшается обратно пропорционально линейному увеличению угла раскрыва заслонки, а воздухообмен через воздушную заслонку апериодически увеличивается прямо пропорционально величине ε. Управление воздухообменом вентилируемого помещения в автоматическом режиме возможно, например, путем изменения угла раскрыва воздушной заслонки в зависимости от температуры внутреннего воздуха.

Заключение

В работе проведен анализ применения полиномиальной регрессии для аппроксимации местного сопротивления воздушной заслонки, выявлены проблемы применения данного подхода при решении задачи расчета динамики изменения воздухообмена. Рассматриваются модели нелинейных функций аппроксимации и оценка параметров методом линеаризации. Предложена параметрическая модель функции аппроксимации на основе логистической кривой, оптимальные значения параметров которой находятся алгоритмически по критерию минимума среднеквадратического отклонения. Построена математическая модель динамики воздушного режима в виде системы дифференциальных уравнений. Показан пример моделирования воздушного режима вентилируемого помещения с учетом предложенной модели функции аппроксимации. Результаты моделирования могут быть использованы при проектировании и настройке регулируемых параметров систем вентиляции.

Библиографическая ссылка