В условиях быстро меняющейся среды внедрение новых технологий автоматизации требует разработки оптимальных стратегий управления различными техническими системами. С увеличением отказов возникают значительные экономические потери, что представляет серьезную угрозу для промышленного и гражданского производства. Для обеспечения эффективности новых и усовершенствования старых систем и компонентов активно используются математические подходы, такие как теория надежности, теория вероятностей, математическая статистика и теория случайных процессов.
Основные задачи, решаемые в рамках теории надежности как самостоятельной научной дисциплины, включают анализ процессов, происходящих в системах и их компонентах под влиянием внутренних и внешних факторов; разработку методов оптимального расчета надежностных показателей объектов; прогнозирование отказов и рекомендации по их устранению; определение корреляционных связей между показателями надежности системы; изучение и анализ показателей безопасности, надежности и долговечности; определение сроков и объемов технического обследования в процессе эксплуатации.
Исследования, связанные с этой областью, проводятся регулярно и постоянно совершенствуются. Приведем ряд публикаций, в которых авторы исследуют возможность оптимизации технических систем.
В работе В.М. Волкова и А.А Миронова [1] основным вопросом изучения является возможность оптимизации процедуры неразрушающего контроля.
В статье И.У. Альберта, С.Г. Шульмана [2] авторы используют вероятностный подход, который позволяет оценить надежность каждого элемента системы конструкции отдельно с помощью параметрического и структурно-логического аппарата теории надежности.
При разработке различных строительных систем сразу решается несколько задач, включая оптимизацию элементов конструкции и учет вероятности их функционирования в течение определенного периода времени [3].
Оценка надежности технических систем может быть выполнена двумя способами: первый – с использованием математического аппарата, основанного на законах распределения, второй – с помощью моделирования готовой системы и проведения различных симуляций [4].
Математическая оценка является быстрым и недорогим способом, но у нее есть недостатки. Она требует знания вероятностей отказов всех элементов системы для достижения точных результатов. Такая информация часто отсутствует для систем, смоделированных на компонентном уровне. Однако у моделирования системы также есть свои ограничения, связанные с ограниченным объемом памяти. Поэтому возможным решением проблемы может быть комбинирование сильных сторон обоих методов и разработка компьютерной программы на их основе.
Существуют различные методы надежностной минимизации рисков отказов [5, 6], которые используются для снижения рисков отказов. Изучение моделей эволюции систем надежности может производиться в определенном временном промежутке с использованием полумарковских процессов. Характеристики полумарковских процессов являются параметрами и характеристиками надежности системы [7].
В анализе надежности системы часто используется количественный показатель организационно-технологической надежности, который имеет вероятностный характер [8]. С использованием элементарных операций теории вероятности проводится анализ надежности разработки решений и обеспечение надежности функционирования системы [8].
Расходы на эксплуатацию, изготовление и ремонт случайных неисправностей играют все большую роль в оценке надежности и вопросе оптимизации стоимости технической системы [9]. Традиционные модели надежности не всегда могут полностью описать работу системы, поэтому может потребоваться их корректировка в зависимости от конкретной задачи.
Например, в статье «Исследование возможности определения вероятности безотказной работы, распределенной радиопеленгационной системы наблюдения с учетом деградации» [10] авторов А.П. Журкова, Д.В. Мирошниченко и др. интенсивность отказов заменяется функцией, связанной со стохастическими наработками и коэффициентами деградации. Данные изменения позволяют вычислить вероятностное значение после n-го восстановления.
В работе «Estimation of Stress-Strength Reliability Model Using Finite Mixture of M-Transformed Exponential Distributions» [11] авторы Adil H. Khan и T.R. Jan исследуют надежность по напряжению и прочности с использованием экспоненциального распределения и его модификации. Изучение показало, что в случае двухкомпонентной системы надежность может иметь как монотонно возрастающую, так и монотонно убывающую функцию, в зависимости от значений параметров. Правильный выбор исходных данных с использованием метода максимального правдоподобия может привести к достижению высоких показателей надежности.
Оценка надежности может быть сложной, особенно при наличии большого числа компонентов в системе, но применение полумарковской модели может значительно упростить анализ [12]. В исследовании J. Soszynska [12] предлагается определение точных и предельных функций надежности при различных условиях эксплуатации, а также строится совместная модель функционирования системы на основе полумарковского процесса и многосоставной совокупности надежности и риска. Результатом данного исследования является разработка оптимальной модели, которая позволяет анализировать работоспособность системы с учетом изменений в структуре надежности в процессе эксплуатации.
Вместе с традиционными моделями надежности широко используются и их изменения, которые адаптированы для конкретных задач. Особый акцент делается на информатизацию и компьютерное моделирование надежности, с использованием математических методов и программного обеспечения. Оценка надежности активно исследуется на стадиях проектирования и эксплуатации, а также учитывается финансовый аспект системы, включая доходы и расходы системы.
Целью работы является построение оптимальной стратегии управления модели надежности технической системы с мгновенной индикацией отказа с учетом экономических показателей системы. В работе определяется оптимальная стратегия управления системой при выборе различных функций распределения, характеризующих работу системы.
Материалы и методы исследования
Часто при разработке математических моделей вводится понятие стратегии. Под стратегией подразумевается правило принятия конкретных решений, то есть управление системой.
Для управляемого случайного процесса ставится задача выбора оптимальной стратегии управления. Так как количественный показатель качества управления должен иметь связь с конкретной траекторией течения процесса, каждой траектории необходимо поставить в соответствие число, характеризующее качество управления. Это означает, что на траекториях случайного процесса строится некоторый функционал.
Для построения управляемого полумарковского процесса применим следующий алгоритм [13, с. 139; 14, с. 545]: сначала определяем марковские моменты, затем определяем состояния системы, далее определяется множество управлений системы и, наконец, проводится построение управляемого полумарковского ядра.
Известно, что для задания управляемого полумарковского процесса задается трехмерная марковская цепь
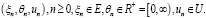
Во введенных обозначениях считаем:
− 
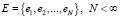– конечное множество состояний (в дальнейшем часто множество Е будем отождествлять с множеством 
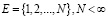), первая компонента ξn однородного управляемого процесса марковского восстановления принимает дискретные значения из этого множества;
− R+ = [0,∞) – множество положительных действительных чисел, поэтому вторую компоненту θn однородного управляемого процесса марковского восстановления отождествляем со временем, на пространстве R+ = [0,∞) задаем борелевскую σ-алгебру;
− U – есть пространство управлений с σ-алгеброй A подмножеств этого пространства.
Однородная марковская цепь (ξn , θn , un) определяется переходными вероятностями
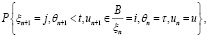
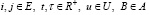
и начальным распределением
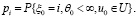
Марковская цепь задается переходными вероятностями, которые называются полумарковским ядром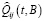 
:
,
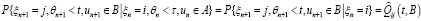для которого выполняется ряд свойств, в том числе:
,
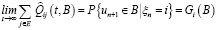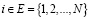и 
, 
.
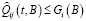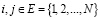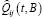порождает условную меру в пространстве управлений. По теореме Радона – Никодима, если 
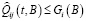, то существует функция Qij(t,u) такая, что
.
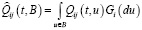Для построения полумарковского ядра воспользуемся следующим определением. Полумарковское ядро – условная вероятность того, что полумарковский процесс перейдет в состояние j и время до этого перехода не превзойдет t при условии, что процесс пребывает в состоянии i и в этом состоянии принято решение из множества управлений:
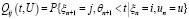.(1)
Таким образом, управляемый полумарковский процесс может быть задан с помощью задания семейств матриц Qij(t,u) и вектора набора вероятностных мер Gi.
Рассматривается модель с мгновенной индикацией отказа, то есть полагаем, что отказ проявляется мгновенно. Введем обозначения: ξ – время безотказной работы, η – время, через которое принудительно заменяется элемент системы.
Тогда функции распределения имеют вид
, 
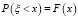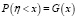(2)
Описание обслуживания заключается в следующем: если η > ξ, то в системе происходит внеплановое, аварийное, полное обновление в момент ξ; если η < ξ, то в системе в момент η проводится плановое, предупредительное, полное обновление системы.
Среди профилактических работ в системе возможны следующие: плановый ремонт, аварийный ремонт.
В качестве марковских моментов рассматривается последовательность моментов начала и окончания восстановительных работ.
Множество состояний системы задается следующим образом: E = {0,1,2}, где {0} – система пребывает в работоспособном состоянии, {1} – система пребывает в плановом ремонте, {2} – система пребывает во внеплановом аварийном ремонте.
Определим множество управлений. В состоянии {0} в качестве множества управления можно задать: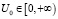 
, то есть определяется время, через которое проводится восстановительная работа (любое из заданного промежутка). В состояниях {1}, {2} никаких решений не принимается, таким образом: 
, 
.
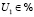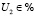Матрица полумарковского ядра Qij(t,u) имеет вид
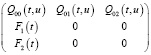, (3)
где
Q00(t,u) = 0
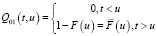(4)
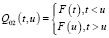. (5)
Для переходов, в которых отсутствует зависимость от управления, верны равенства
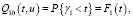(6)
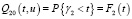. (7)
При проверке свойств полумарковского ядра нетрудно заметить, что
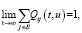(8)
где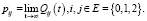 
Таким образом, полумарковское ядро построено верно.
Результаты исследования и их обсуждение
Чтобы количественно оценить качество управления, необходимо установить связь с конкретной траекторией процесса. Для этого каждой траектории назначается числовое значение, отражающее качество управления. Это означает, что на основе траекторий процесса строится некий функционал. Хотя возможность появления конкретной траектории связана с вероятностью, функционал, который представляет его значение, является случайной величиной. Поэтому можно воспользоваться числовыми показателями, такими как математическое ожидание, которые позволяют установить порядок на множестве таких показателей. Построим функционал: траектории или ее части в соответствие ставится число.
Для построения функционала накопления найдем функции Rij(t,u), которые есть математическое ожидание накопленного эффекта (дохода) за весь период t, при условии, что процесс находится в состоянии i, следующим состоянием будет состояние j, при условии, что в момент перехода было принято решение u.
Для построения функции Rij(t,u) необходимо ввести величины, определяющие доходы и расходы системы: c0 – доход за единицу времени, ci – расход за единицу времени, i = 1,2.
R01(t,u) = R02(t,u) = c0t, (9)
R10(t,u) = c1t, c1 < 0, (10)
R20(t,u) = c2t, c2 < 0. (11)
Данные показатели и их количество могут варьироваться в зависимости от системы и цели исследования.
По формуле полного математического ожидания получаем систему интегральных уравнений [14]:
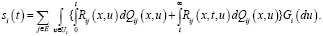(12)
Нахождение математического ожидания si накопленного дохода за полный период пребывания процесса в состоянии i выполняется по формуле 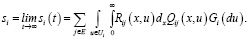[13]:
(13)
Соответственно, для i = 0,1,2 имеем
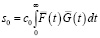, (14)
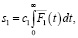(15)
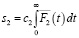. (16)
Для того чтобы определить mi – математическое ожидание времени непрерывного пребывания процесса в состоянии i, необходимо воспользоваться формулой [13]:
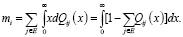(17)
Соответственно, для i = 0,1,2 имеем
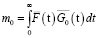, (18)
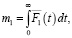(19)
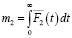, (20)
Для нахождения аналитической формулы функционала накопления воспользуемся теоремой о виде функционала накопления, построенного на траекториях управляемого полумарковского процесса [13, 14]:
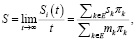(21)
где si , mi < ∞ определены равенствами выше, а πk – стационарные вероятности распределения состояний вложенной цепи Маркова, то есть нормированное решение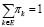 
алгебраической системы уравнений
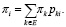(22)
При решении системы получаем: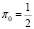 
, 
, 
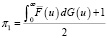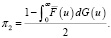
Выражение для функционала накопления имеет следующий вид:
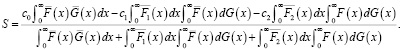(23)
Отметим, что по теореме о максимуме дробно-линейного функционала, если существует максимум дробно-линейного функционала [14], то он достигается на множестве вырожденных распределений, то есть оптимальная стратегия управления ищется в классе детерминированных стратегий:
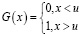. (24)
При подстановке вырожденного распределения в получившийся функционал получаем
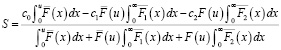. (25)
Таким образом, задача сводится к определению максимума функции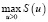 
и точки u0, в которой достигается этот максимум. Значение точки максимума определяет, через какое время следует назначать ремонтные работы.
Рассмотрим поиск оптимальной стратегии для различных классических моделей надежности.
В экспоненциальной модели надежности интенсивность отказов является постоянной величиной: λ(t) = λ = const, λ > 0, а время до наступления отказа считается непрерывной случайной величиной, которая распределена по экспоненциальному закону. Вероятностная функция отказа записывается в виде Q(t) = 1 – e–λt.
Несложная зависимость между показателями надежности, а также возможность элементарного расчета сложных систем являются основными преимуществами экспоненциальной модели. Например, ей отдается предпочтение, если производится сортировка брака перед поступлением товара в продажу.
В модели надежности Рэлея время до наступления отказа – непрерывная случайная величина, которая распределена по закону Рэлея:
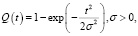(26)
где σ – это определенный коэффициент распределения, у которого временная размерность. Из характерной формы интенсивности определяются условия для применения данной модели – это отказы систем механики (из-за сил трения интенсивность постоянно растет) или моделирование процессов износа.
В модели надежности Вейбулла время до отказа – это непрерывная случайная величина, имеющая распределение Вейбулла:
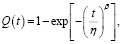(27)
η, β > 0, где β – безразмерный параметр формы, η – параметр масштаба, измеряемый в единицах времени (часах).
Форменный параметр β в большей степени влияет на характер функций плотности и интенсивности отказов: при β > 1 происходит монотонное возрастание функции интенсивности, а функция плотности имеет характерный «горб»; при β < 1 происходит монотонное убывание функции интенсивности и функции плотности отказов.
Своеобразная простота модели надежности Вейбулла сделала ее профессиональным стандартом качества в области надежности. Она имеет свои недостатки, но при этом широко применяется для анализа и расчета надежностных показателей технических систем.
Для примера нахождения оптимальной стратегии рассмотрим несколько вариантов распределений рассматриваемой системы.
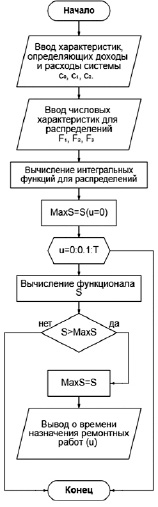
Блок-схема алгоритма решения для поиска оптимальной стратегии в технической системе с мгновенной индикацией отказа
Для модели с мгновенной индикацией отказа полагаем, что функция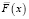 
имеет распределение Вейбулла, вероятность безотказной работы которого равна
,
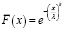где коэффициент масштаба λ = 1 (интенсивность отказов не меняется во времени), а коэффициент формы k = 2. Функци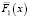и 
и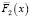 
имеют показательное распределение, для которого вероятность безотказной работы имеет вид 
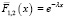, с интенсивностью λ = 2, λ = 3 соответственно.
В качестве показателей, определяющих расходы и доходы системы, выберем следующие произвольные числовые значения в условных единицах измерения: доход за единицу времени c0 = 10 у.е., расход за единицу времени c1 = 3 у.е., расход за единицу времени c2 = 2 у.е.
Аналитический вид функционала для данной задачи:
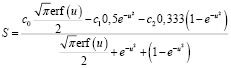. (28)
Таким образом, получен функционал, зависящий от переменной, отвечающей за управление. Далее следует определить максимум функционала по u.
Приведем блок-схему (рисунок) для поиска оптимального значения и созданную по ней программную реализацию. Программная реализация может быть осуществлена по данному алгоритму в любой программной среде.
При заданных показателях при реализации программы в качестве оптимального получено значение u = 6,1, в котором достигается максимум данного функционала 8,5. Следовательно, через это условное время будет целесообразным назначить проведение профилактических работ. Варьируя параметрами c0, c1, c2, можно наблюдать, как меняется значение u. Так, например, для c0 = 20, c1 = 4, c2 = 7 значение u = 5,9.
При рассмотрении модели с мгновенной индикацией отказа, у которой функция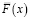 
имеет распределение Рэлея, вероятность ее безотказной работы равна
,
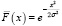с параметром σ = 2. Функци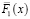и 
и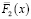 
имеют показательное распределение, для которого вероятность безотказной работы имеет вид 
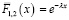, где коэффициент масштаба λ = 2, λ = 3 соответственно.
При подстановке соответствующих распределений получаем аналитический вид функционала:
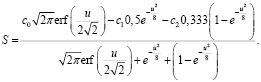(29)
При выборе значений доходов и расходов c0 = 10 у.е., c1 = 3 у.е., c2 = 2 у.е. оптимальное значение достигается при u = 16,9, в котором достигается максимум данного функционала.
Рассмотрим модель с мгновенной индикацией отказа, у которой функция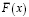 
имеет показательное распределение, вероятность ее безотказной работы равна 
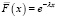, с интенсивностью λ = 0,5. Функци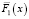и 
и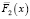 
имеют распределение Вейбула, для которого вероятность безотказной работы имеет вид
,
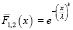где коэффициент масштаба λ = 2, λ = 3, коэффициенты формы k = 3, k = 2.
При подстановке соответствующих распределений получаем аналитический вид функционала:
.
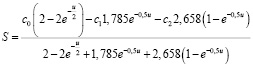При выборе значений доходов и расходов c0 = 10 у.е., c1 = 3 у.е., c2 = 2 у.е. в результате вычислений получаем значение u = 74,9, в котором достигается максимум данного функционала, равный 3,15. В случае отклонения от оптимальной стратегии и выбора другого значения переменной выбранный показатель эффективности работы системы снижается. Так, например, при выборе значения u = 5 значение показателя будет равно 2,94.
В случае отклонения от оптимальных стратегий управления показатель эффективности работы системы снижается вне зависимости от вариантов выбранных распределений рассматриваемой системы.
Заключение
Получена аналитическая формула функционала дохода технической системы с мгновенной индикацией отказа, на ее основе возможно нахождение оптимальной стратегии управления временем проведения ремонтных работ в зависимости от выбранных функций распределения, а также показателей дохода и расходов системы, которые могут варьироваться.
Используя теорию управляемых полумарковских процессов, можно исследовать различные задачи оптимального технического обслуживания систем, как с учетом их структуры, так и без него. При этом для каждой технической системы на этапе ее разработки и конструирования должны быть регламентированы правила технического обслуживания, позволяющие функционировать системе максимально эффективно.
Библиографическая ссылка
Кондрашова Е.В., Шепелев А.С. О ПОИСКЕ ОПТИМАЛЬНЫХ СТРАТЕГИЙ УПРАВЛЕНИЯ ТЕХНИЧЕСКИМИ СИСТЕМАМИ // Современные наукоемкие технологии. – 2024. – № 1. – С. 47-54;URL: https://top-technologies.ru/ru/article/view?id=39907 (дата обращения: 19.05.2024).