Для анализа особенностей распространения сигналов в информационных каналах различного назначения часто используется модель канала с бесконечной кривизной [1; 2; 3, c. 15; 4, с. 21]. Данное приближение в ряде случаев вполне оправдано и существенно упрощает расчет характеристик сигнала путем введения декартовой системы координат. Между тем известны задачи, когда учет конечной кривизны канала имеет принципиальное значение. Например, при распространении сигналов на космических трассах необходимо принимать во внимание кривизну поверхности Земли, сферичность околосолнечной и межзвездной среды.
Эффективным методом расчета характеристик сигналов в информационных каналах является приближение геометрической оптики [5, c. 140]. При кажущейся простоте и наглядности геометрической оптики решение лучевых дифференциальных уравнений в возмущенных условиях вызывает затруднение даже в случае бесконечного радиуса кривизны канала. Тем более не представляется возможным получить точное аналитическое решение системы нелинейных дифференциальных уравнений первого порядка в канале с конечной кривизной. Между тем решение лучевых уравнений можно найти путем их численного интегрирования каким-либо из хорошо апробированных численных методов [6, с. 237]. Применение численного интегрирования в ряде случаев оказывается более продуктивным по сравнению с использованием упрощенных аналитических расчетов. Более того, с помощью численных расчетов можно визуализировать зависимости характеристик сигнала в широком диапазоне начальных параметров задачи.
Цель настоящей работы заключается в создании эффективной вычислительной схемы расчета рефракционных искажений сигнала в возмущенном информационном канале с конечной кривизной.
Основные аналитические соотношения
Для расчета траекторных характеристик и рефракционного ослабления потока энергии сигнала в возмущенном информационном канале использовалась расширенная система лучевых дифференциальных уравнений [5, с. 159]:
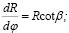
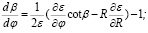
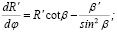(1)
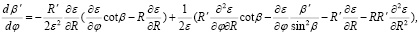
где R, φ – радиальная и угловая координаты луча; β – угол рефракции; ε(R,φ) – диэлектрическая проницаемость канала;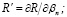 
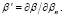
Рефракционное ослабление потока энергии сигнала оценивалось с помощью фактора фокусировки:
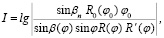(2)
где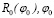 
– радиальная и угловая координаты луча при распространении в невозмущенном информационном канале.
Для тестирования численных расчетов важно иметь аналитическое решение системы (1) в некотором частном случае. Проводя в системе (1) замену переменных: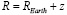 
, 
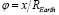и выполняя предельный переход 
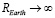, получаем систему дифференциальных уравнений в плоском случае. Эта система допускает точное аналитическое решение для модели диэлектрической проницаемости вида
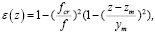(3)
где fcr – критическая частота; zm – высота минимума диэлектрической проницаемости;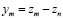 
– полутолщина слоя; zn – высота начала слоя. С учетом закона Снеллиуса [5, с. 153]:
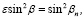– (4)
решение системы (1) имеет вид
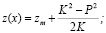
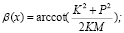
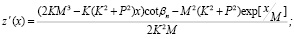(5)
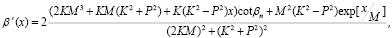
где βn – начальный угол излучения,
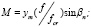
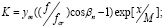
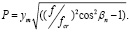(6)
Решения (5), (6) получены в случае, когда источник сигнала находился в канале на высоте zn.
Тестирование вычислительной схемы
Тестирование численных расчетов было выполнено при начальных условиях:
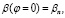
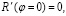
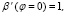
угол βn изменялся в секторе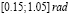 
. Источник сигнала находился в точке 
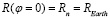. Высота минимума диэлектрической проницаемости 
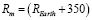км, критическая частота fcr = 9 МГц. Результаты моделирования представлены на рис. 1, откуда следует, что при распространении сигнала в слоистом информационном канале кривые, рассчитанные с помощью численной схемы и по аналитическим формулам (5), (6), совпадают с хорошей точностью.
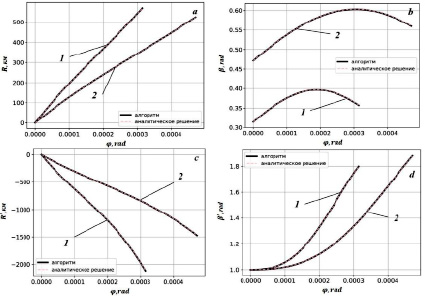
Рис. 1. Сравнение численных и аналитических расчетов рефракционных характеристик сигнала: a – R(φ); b – β(φ); c – R′(φ); d – β′(φ), – при различных значениях прицельного параметра βn: 0.314 rad (1) и 0.473 rad (2)
Моделирование показало, что порядок расхождения кривых на рис. 1 составляет в среднем 10–4 rad. Таким образом, численная схема расчета системы обыкновенных дифференциальных уравнений первого порядка может быть использована для математического моделирования рефракционных характеристик сигналов в возмущенных информационных каналах с более сложными аналитическими функциями диэлектрической проницаемости.
Численные эксперименты
С использованием предложенной схемы расчета были поставлены численные эксперименты. Прежде всего, был рассмотрен канал передачи сигнала в околоземном пространстве. На основе (1), (2) рассчитывались зависимости фактора фокусировки сигнала на различных рабочих частотах. Модель диэлектрической проницаемости возмущенного канала задавалась в виде [7, с. 480]:
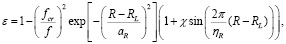(7)
где RL – радиальная координата максимума ионизации ионосферы; aR – полутолщина ионосферного слоя; χ, ηR – интенсивность и длина волны (в км) возмущения соответственно. Результаты расчетов фактора фокусировки представлены на рис. 2.
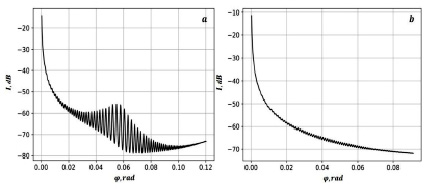
Рис. 2. Динамика фактора фокусировки сигнала в ионосферном канале на различных рабочих частотах:f1 = 13 МГц (a) и f2 = 19 МГц (b). fcr = 9 МГц; RL = 6721 км; aR = 290 км; χ = 0.5; ηR = 10; βn = 0.66 rad
Из рис. 2 следует, что в зависимости от рабочей частоты сигнала в ионосферном канале возникают особенности в распределении значений фактора фокусировки. В случае более низкой частоты (рис. 2, а) хорошо видны осцилляции амплитуды, связанные с колебаниями критической частоты ионосферы, вызванные волнообразным возмущением электронной плотности. Глубина этих осцилляций определяется близостью возмущенных траекторий к траекториям в свободном пространстве. Для более высокой рабочей частоты сигнала (рис. 2, б) отмечается малая глубина осцилляций амплитуды, что связано с уменьшением воздействия волнообразного возмущения на распространение сигнала. Следует заметить, что в рассматриваемых случаях осцилляции амплитуды связаны именно с колебаниями критической частоты ионосферы, а не с образованием областей фокусировок. Расчеты, проведенные на основе уравнений (1), (2), показали отсутствие участков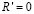 
на траекториях сигнала.
Другой численный эксперимент был поставлен для канала просвечивания околосолнечной плазмы в условиях коронального выброса массы (КВМ) [8]. Модель диэлектрической проницаемости возмущенного канала задавалась в виде
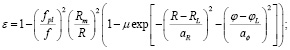(8)
где fpl – плазменная частота на некотором расстоянии Rm = 5Rs от центра Солнца; Rs – радиус Солнца; μ – безразмерный параметр полости КВМ; RL, φL – радиальная и угловая координаты центра КВМ; aR, aφ – радиальный и угловой масштабы коронального возмущения соответственно.
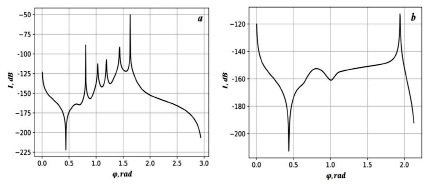
Рис. 3. Фактор фокусировки сигнала в канале просвечивания околосолнечной плазмы для f1 = 25 МГц (a) и f2 = 35 МГц (b) fpl = 19 МГц; μ = 1.7; RL = 5Rs; φL = 0.4 rad; aR = 0.15Rs; aφ = 0.63 rad; βn = –0.42 rad
На рис. 3 представлены результаты расчетов на основе (1), (2) фактора фокусировки сигнала в околосолнечной плазме на различных рабочих частотах. На более низкой частоте f = 25 МГц (рис. 3, а) видны последовательные осцилляции фактора фокусировки, связанные с волноводным распространением сигнала в полости КВМ. Волноводный механизм распространения сигнала возможен на низких рабочих частотах, когда воздействие окружающей плазмы значительно. На более высоких частотах (рис. 3, б) можно отметить участок, связанный с проникновением сигнала в полость КВМ и выходом из нее. Между тем рефракционного волновода в таких условиях не возникает. Следует также отметить, что пути распространения сигналов в возмущенном канале на различных рабочих частотах существенно отличаются.
Также был поставлен численный эксперимент для канала распространения сигнала в межзвездной среде в окрестности массивных гравитационных объектов. Одним из следствий общей теории относительности (ОТО) [9, с. 172] является то, что процесс распространение волн в искривленном (римановом) пространстве можно приближенно представить как процесс распространения волн в эвклидовом пространстве с эффективным показателем преломления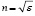 
, учитывающим гравитационный потенциал объекта. Для расчета влияния гравитационного поля на рефракционные характеристики сигнала в канале в межзвездной среде, использовалась модель диэлектрической проницаемости вида
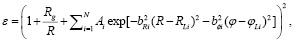(9)
где Rg – гравитационный радиус основного объекта; N – количество дополнительных объектов;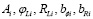 
– соответственно доля вклада, координаты локализации и масштабы возмущения показателя преломления, вызванного i-м объектом.
На рис. 4 представлены результаты расчета фактора фокусировки сигнала на основе уравнений (1), (2). В определенных диапазонах начальных углов излучения нетрудно заметить появление ряда осцилляций. Такие осцилляции возникают вследствие влияния системы гравитационных объектов. В результате образующегося гравитационного волновода существенно возрастает путь сигнала в канале межзвездного пространства. Также существуют диапазоны начальных углов излучения сигнала, в которых эффекты влияния гравитационного поля группы объектов относительно малы, что соответствует распространению сигнала вблизи одного из объектов.
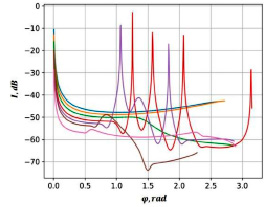
Рис. 4. Результаты расчетов фактора фокусировки сигнала при распространении в межзвездной среде в окрестности группы гравитационных объектов
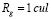(cul – условная единица длины);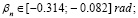
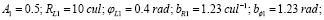
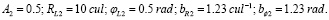
Заключение
Приведены результаты математического моделирования траекторных характеристик и рефракционного ослабления потока энергии сигнала в возмущенном информационном канале с конечной кривизной. Численные расчеты выполнены в лучевом приближении и основаны на интегрировании обыкновенных дифференциальных уравнений первого порядка. Для простой слоистой модели диэлектрической проницаемости канала получены аналитические решения для траекторных характеристик и лучевой расходимости сигнала. Проведена проверка результатов математического моделирования путем их сравнения с результатами аналитических расчетов. Проверка показала высокую точность численного интегрирования дифференциальных уравнений. Предложенная численная схема расчета достаточно универсальна и допускает включение дополнительных дифференциальных уравнений для расчета групповой и фазовой задержек сигнала. Представлены примеры реализации вычислительной схемы для решения задач распространения сигналов в возмущенных каналах с конечной кривизной. С помощью численных расчетов выявлены особенности рефракционных искажений трансионосферных сигналов под воздействием волнообразных ионосферных возмущений, показана возможность наземного наблюдения сигнала залимбового радиоисточника в случае образования в солнечной короне области пониженной электронной плотности и рассчитана сложная интерференционная картина поля сигнала при его распространении в гравитационном поле группы гравитационных объектов в межзвездной среде.
Библиографическая ссылка
Ким Д.Б., Афанасьев Н.Т., Лукьянцев Д.С., Ситов И.С., Танаев А.Б., Чудаев С.О. РЕФРАКЦИОННЫЕ ИСКАЖЕНИЯ ХАРАКТЕРИСТИК СИГНАЛА В ВОЗМУЩЕННОМ ИНФОРМАЦИОННОМ КАНАЛЕ С КОНЕЧНОЙ КРИВИЗНОЙ // Современные наукоемкие технологии. – 2023. – № 12-2. – С. 203-209;URL: https://top-technologies.ru/ru/article/view?id=39882 (дата обращения: 20.05.2024).