Ввиду очевидной важности математики в современном мире математика должна изучаться, осваиваться и быть понятой учащимися. Однако результаты обучения математике в школах и в вузах все еще не оптимальны, о чем можно судить по количеству обучающихся, испытывающих трудности в изучении математики.
На решение математических задач влияет множество факторов, вызывающих у студентов затруднения. Одним из таких факторов являются ошибки студентов при решении задач по математике. Трудности в решении математических задач неотделимы от ошибок, которые студент совершает. Ошибки – это отклонения от правильных действий, которые носят различный характер, в том числе случайный. К систематическим ошибкам можно отнести ошибки, которые носят устойчивый характер [1]. В то время как случайная ошибка – это ошибка, которая не обусловлена уровнем усвоения материала, а вызвана другими причинами, например небрежностью, меньшей аккуратностью при чтении или счете, поспешностью в работе и т.д.
Цель обучения математике состоит не столько в приобретении методов, позволяющих обучающимся по известным алгоритмам решать примеры и задачи, сколько в том, чтобы обучение приводило к пониманию обучающимися математики. В качестве инструментов для анализа когнитивных процессов, посредством которых учащиеся развивают математическое мышление, служат различные теории, направленные на создание условий для осмысленного обучения. Для нашего исследования представляет интерес теория APOS, которая позволяет изучать процессы структуризации математических понятий в сознании обучающегося, определять и классифицировать ошибки. Основная цель теории APOS – выявить, как математическая концепция структурируется в сознании человека. Ментальные структуры, сформированные на основе рефлектирующей абстракции [2], были названы в теории APOS Action (Действие), Process (Процесс), Object (Объект), Scheme (Схема). Эта теория впервые была проверена на исследовании понятия смежных классов в теории групп [3], получила продолжение в теории моделирования и экономике [4] и в других областях.
Теория APOS концентрируется на построении этапов, разъясняющих происходящие у обучающегося ментальные процессы, когда он пытается понять ту или иную математическую концепцию. Арнон и др. [5, с. 10] полагают, что «APOS – это теория того, как математические понятия могут быть выучены». Подробная информация по использованию теории APOS в обучении математике содержится в обзорной работе [6].
Большие трудности в понимании у студентов вызывает как понятие функции вообще, так и понятие тригонометрической функции в частности. Выбор в качестве предмета применения теории APOS тригонометрических функций обусловлен их значимостью в математике, физике и широким использованием в инженерном деле. Тригонометрические функции вводятся в практику обучения тремя способами, а именно: через соотношения в прямоугольном треугольнике, через использование единичной окружности, а также аналитически через степенные ряды. Такая множественность в определении накладывает свой отпечаток в понимании и вызывает трудности, приводящие к разнообразным ошибкам [7]. Для преодоления этих трудностей предлагаются методологические подходы, например метод проблемного обучения [8], а также создаются различные методы решения типовых тригонометрических уравнений и их применений в геометрии [9].
В большинстве работ по методике преподавания математики основное внимание уделяется внешнему плану в восприятии обучающимися математического понятия, хотя очевидно, что чрезвычайно важной является изучение структур, сформированных в сознании обучающегося в процессе познания математического понятия. Важность проблемы мониторинга динамики развития индивидуальных качеств обучающихся подчеркивал и В.А. Гусев [10]. В этом направлении в последние годы увеличивается число работ (особенно зарубежных, например обзор [6]), из отечественных отмечена работа [11].
Основная идея предлагаемой работы заключается в том, чтобы использовать теорию APOS к исследованию формирования ментальных структур обучающихся на примере тригонометрических функций, что позволит выделить этапы восприятия студентом математического понятия, исследовать природу и характер ошибок, совершаемых студентами на каждом этапе.
Цель предлагаемого исследования состоит в классификации математических ошибок (на примере тригонометрических функций) с использованием теории APOS. Для достижения указанной цели необходимо решение следующих задач:
− описание на основе теории APOS восприятия студентами понятия тригонометрической функции;
− анализ ошибок, допускаемых студентами, и их классификация в рамках теории APOS.
Материалы и методы исследования
В данной работе теория APOS, развитая Э. Дубинским с коллегами [5, с. 12], рассматривается в качестве теоретической основы.
Теория Action – Process – Object – Schema (APOS) представляет собой адаптацию идей Пиаже [2] о рефлектирующей абстракции для моделирования построения учащимися ментальных структур, необходимых для понимания математики (подробнее [5, с. 17]). В APOS Действие – это преобразование ранее построенного математического объекта, которое индивид воспринимает как внешнее. Действия основаны на правилах и алгоритмах, отрабатываемых многократно и проводимых под руководством преподавателя, но привязанных к конкретным объектам. В случае тригонометрических функций студент должен уметь отличать тригонометрические функции от других функций, вычислить значение тригонометрической функции в какой-то точке.
Когда действие повторяется, а индивид реагирует на него, оно может интериоризироваться в Процесс, то есть переходить из внешнего плана во внутренний. Он будет иметь содержательные связи с другими математическими знаниями, что позволит обучающемуся представить себе Процесс и предвидеть результаты, не выполняя его в явном виде. На стадии Процесса вычисления значений функции для любого угла студент делает без посторонней помощи.
При изменении контекста, в котором индивид конструирует Процесс, он может почувствовать необходимость в выполнении действий над процессом, чтобы осмыслить новые проблемные ситуации. Для этого индивид должен воспринимать процесс как целостность, как сущность саму по себе. Когда обучающийся способен выполнять действия над процессом или представлять себе действия над процессом, можно сказать, что процесс инкапсулирован [5, с.18] в Объект. В случае тригонометрических функций это означает, что студент может выделить, например, интервалы возрастания и убывания функций.
Действия, процессы, объекты и другие, ранее созданные ментальные структуры, связанные с конкретным математическим понятием, могут быть организованы в целостную структуру, называемую схемой. Схема приводится в действие в ответ на проблемную ситуацию, которую индивид воспринимает как проявление конкретного математического понятия.
Исследование авторов в соответствии с теорией APOS направлено на сбор и анализ данных с последующим разбором ошибок, демонстрируемых студентами на каждой из стадий, рекомендациями по их исправлению. В данной работе принято в соответствии с исследованиями [6] ошибки подразделять на концептуальные и процессуальные. Такой подход к анализу ошибок с применением теории APOS при изучении темы «Дифференцирование», как показано, например, в работе [12], оказался весьма эффективным.
Концептуальные ошибки свидетельствуют о неспособности понять смысл задачи, неспособности оценить взаимосвязи в задаче, а также отношения между понятиями. Концептуальное понимание становится основой для решения математических и контекстуальных задач. Уровень понимания концепции относится к способности человека всесторонне понимать идеи, процедуры и факты, которые образуют сеть мышления с разнообразными взаимосвязями. Процессуальные ошибки возникают, когда учащиеся не выполняют манипуляции или алгоритмы, они показывают неспособность обучающегося правильно проводить преобразования технического, формального характера, даже если концепции понятны.
Концептуальное понимание в нашем случае означает, что студент свободно владеет различными представлениями тригонометрических функций (алгебраическими, графическими, понимает тригонометрические соотношения в прямоугольном треугольнике), может легко переходить от одной формы к другой и знает связи между различными тригонометрическими формулами. К концептуальным ошибкам можно отнести непонимание понятия функции, неумение распознавать свойства сложных тригонометрических функций на основе знаний свойств основных элементарных тригонометрических функций.
Эмпирический этап исследования был проведен на базе Казанского государственного архитектурно-строительного университета. В нем приняли участие 102 студента из групп первого курса направления подготовки «Строительство». Все респонденты на момент участия в исследовании были проинформированы о цели исследования и выразили готовность к сотрудничеству. Исследование проводилось поэтапно. На первом этапе (теоретическом) были уточнены концептуальные вопросы исследования, научно обоснованы и разработаны основные разделы опросника, позволяющие проверить готовность студентов к пониманию и оценить стадии понимания математических объектов согласно теории APOS. Применялись методы системного анализа литературы по обозначенной проблеме, методы статистической обработки информации. На втором этапе (экспериментальном) производился опрос, в котором респондентам предлагалось выполнить задания разработанного на первом этапе опросника, направленного на выявление ошибок и уяснения того, на какой стадии понимания понятия находится тот или иной студент.
Третий этап включал количественную и качественную обработку результатов (с применением методов аналитической группировки, контент-анализа и математической статистики) и их систематизацию и интерпретацию.
Результаты исследования и их обсуждение
Анализ письменных работ, проведенных в рамках эксперимента, позволил сформулировать методические «пустоты» в изучении соответствующего раздела математики. Авторами представлены ошибки, совершаемые студентами, отдельно по каждой стадии APOS, по вопросам, разработанным для каждой стадии.
Для выяснения ошибок на уровне Action stage были заданы два вопроса: «1. Напишите чему равно: sin(π/2), sin(π/3), sin30°. 2. Запишите в порядке возрастания чисел sin115°, sin250°, sin370°». При этом, как показал опрос, проведенный авторами статьи, эти знания студентами поняты и освоены хорошо, ошибки преимущественно носят процессуальный характер. Студенты справились с заданиями этой стадии преимущественно без ошибок, особенно при работе с табличными значениями (98,2 и 77,4 % опрошенных по каждому вопросу соответственно). 0,9 и 17,6 % допустили процессуальные ошибки по двум вопросам соответственно. Концептуальные ошибки совершили 0,9 и 7 % по каждому из двух вопросов.
Process stage возникает при изучении тригонометрических функций, когда вводится понятие единичного круга, с помощью которого изучаются некоторые свойства этих функций. Стадия Process представлена тремя вопросами: «1. Для каких x функция синус убывает, почему? 2. Верна ли формула sin(x + y) = sinx ∙ siny ? Если нет, напишите правильную формулу. 3. Покажите на единичном круге решение уравнений: sinx = 0.5, sinx = 1, sinx = 1,5». На этой стадии количество концептуальных ошибок выросло по сравнению с предыдущей стадией. Авторами установлено, что хуже всего студенты владеют свойствами функции синуса и формулами, связывающими тригонометрические функции, эти вопросы сопровождаются и концептуальными, и процессуальными ошибками. Так, 6,8; 33,6 и 32,3 % соответственно по каждому вопросу этой стадии имеют концептуальные ошибки, 8,9 и 25,5 % имеют ошибки процессуальные, т.е. технического характера.
Стадия Object представлена тремя заданиями: «1. Опишите своими словами функцию sinx. 2. Существуют ли x ∈ R, решения неравенства sinx ≥ 1/2 ? Если нет, объясните почему. 3. Что означает периодичность функции sinx и какой у нее период? Какой период функции sin2x?» Опрос по стадии Object показал, что задачи, связанные с применением свойств тригонометрических функций, сопровождаются повышением концептуальных ошибок. На первый вопрос наибольшее количество процессуальных ошибок (90,2 %), это свидетельствует о том, что студенты плохо владеют понятием функция, у них не сформировалось концептуальное понимание этого математического объекта и слабо развиты способности к обобщению и систематизации. В среднем процент концептуальных ошибок составляет 59,8 (от 44,2 до 90,2 %). Процессуальные ошибки на данной стадии возникают лишь в тех задачах, где имеется процесс вычисления, небольшого преобразования, последовательности формальных действий, например, задачи решения неравенств, определения соответствия. Наибольшие трудности возникли у студентов в области теоретического понимания объекта тригонометрической функции, что сопровождается значительным количеством концептуальных ошибок, поэтому, авторы статьи могут утверждать, что данная стадия наиболее слабо представлена в процессе обучения математике.
Стадия Schema связана с глубинным пониманием математического объекта, способностью обобщения полученных результатов, поэтому на этом этапе были предложены вопросы: «1. Чему равно sin2x + cos2x и почему? 2. Постройте график функции y = a ∙ sinx, выразите постоянную a. И на том же графике изобразите график функции y = a ∙ sin3x». Результаты ответа на первый вопрос показывают, что большинство студентов ни показать, ни доказать основное тригонометрическое тождество не могут (84,3 % концептуальных ошибок). Такая же картина вырисовывается и с графическим представлением функции синуса (55,9 % концептуальных ошибок). Тем самым показано, что понятие тригонометрических функций у чуть более чем половины выпускников школ, поступивших в технический вуз, не освоено, преимущественно преобладают концептуальные ошибки, а незначительное число процессуальных ошибок связано с описками технического характера. Последняя стадия, Schema, связана с применением математических понятий для построения новых задач, теоретических или практических, например трансформация графика или вывод формул. Для решения задач этой стадии студент должен не только знать основные свойства объекта, но и применять их. Опрос показал, что доля концептуальных ошибок на этой стадии наибольшая среди остальных стадий и составляет 70,1 %. Процессуальные ошибки присутствуют лишь в задаче, связанной с построением графика, и соответствуют в основном небольшим погрешностям и неаккуратности чертежа.
По результатам исследования приведена общая диаграмма распределения ошибок, относящихся ко всем стадиям APOS (рисунок).
Из рисунка видно, что лучше всего студенты в школе освоили табличные значения, работа с тригонометрическими функциями на окружности ими также освоена и поведение синуса в первой четверти тоже известно.
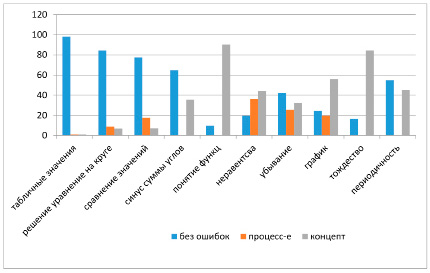
Диаграмма ошибок
Но тригонометрические формулы они знают плохо, только те, что часто использовались в простых задачах по тригонометрии, на это и указывает рост концептуальных ошибок. Однако с теоретическим пониманием функции вообще и функции синуса в частности, у студентов наблюдаются трудности.
Теория APOS, опирающаяся на поэтапное исследование когнитивного процесса, дает возможность преподавателю определить действия обучающихся на каждом этапе познавательного процесса. Подавляющее большинство студентов (в среднем 87,8 %) в изучении тригонометрических функций находится на стадии Action, то есть они способны выполнять простейшие операции с тригонометрическими функциями, знают базовые формулы и табличные значения и способны с помощью преподавателя выполнить задание, требующее применения базовых формул. В результате обработки данных эксперимента установлено, что при переходе от стадии к стадии в среднем число студентов, владеющих пониманием сути понятия тригонометрических функций, снижается. Так, на стадии Action в среднем 87,8 % опрошенных, Process – в среднем около 64 %, Object – 28,1 %, Schema – 20,5 %.
Как показали эксперименты, причиной ошибок является неточное понимание студентами определения функции, неумение делать алгебраические преобразования, плохое и зачастую формальное понимание свойств тригонометрических функций, неумение связать символьную и визуальную области (подтверждает результаты, полученные в работе [13]). Использование теории APOS в данной работе показало, что с помощью этой теории можно не только выявить ошибки, но выделить этапы познавательного процесса и уточнить характер затруднений.
Выводы
Результаты, полученные в данном исследовании, позволяют сделать следующие выводы.
1. Теория APOS дает эффективную возможность выявить и исследовать трудности в понимании математических понятий. Выводы, связанные со снижением от стадии к стадии числа студентов, хорошо знающих математику, подтверждают результаты других работ [12].
2. Ошибки, носящие концептуальный и процессуальный характер, совершаемые студентами в ходе обучения на разных стадиях теории APOS, отличаются своей концентрацией: наиболее часто концептуальные ошибки совершаются на стадиях Object и Schema, а процессуальные – на стадиях Action и Process. Теория APOS позволяет на каждом этапе выявить характер совершаемых студентами ошибок и дает ориентацию на проведение соответствующих методических мероприятий по устранению появившихся трудностей с учетом индивидуальности обучающегося.
3. Практическая значимость исследования, как показано в работе, заключается в том, что с помощью теории APOS можно оценить уровень владения математическими понятиями каждого студента, что дает возможность сделать обучение более продуктивным и в комплексе с другими методами позволяет повысить эффективность образовательного процесса.
Материалы статьи могут быть использованы как школьными учителями математики, так и преподавателями вузов.
Библиографическая ссылка
Туктамышов Н.К., Горская Т.Ю. ОПЫТ КЛАССИФИКАЦИИ МАТЕМАТИЧЕСКИХ ОШИБОК С ИСПОЛЬЗОВАНИЕМ ТЕОРИИ APOS // Современные наукоемкие технологии. 2023. № 12-1. С. 177-182;URL: https://top-technologies.ru/ru/article/view?id=39879 (дата обращения: 14.02.2026).
DOI: https://doi.org/10.17513/snt.39879



