Проведение научных исследований в сфере экономики, финансов, социально-экономических процессов и других смежных отраслей сопряжено с необходимостью анализа больших массивов статистической информации. Трудоемкость данного этапа научных исследований является ключевым фактором, определяющим необходимость использования для решения широкого круга задач анализа статистической информации современных цифровых технологий. В ряде случаев общую картину анализа данных дополняют разработанные математические модели, позволяющие оценивать тенденции динамики исследуемых показателей на протяжении длительного интервала времени, определять количественные характеристики, выявлять и анализировать тесноту связи между различными явлениями и процессами. В ряде научных публикаций авторов разработаны прикладные модели, характеризующие особенности развития различных социально-экономических процессов, с использованием информационных технологий [1, 2].
Одним из популярных языков, широко используемым при решении широкого круга задач анализа данных и машинного обучении, является высокоуровневый язык программирования Рython, возможности которого дополнены фреймворками, значительно расширяющими сферы применения данного языка программирования.
Целью исследования является разработка методики поэтапного анализа и построения математических моделей в среде Рython для решения широкого круга задач анализа статистических данных.
Материалы и методы исследования
В качестве материалов исследования использовались официальные статистические данные, характеризующие развитие Центрального федерального округа за 2005–2022 гг. Методами исследования послужили специальные методы статистического анализа данных в среде Рython, такие как трендовый и корреляционно-регрессионный анализ, метод выборочного наблюдения, сводки и группировки, а также комплексный системный анализ социально-экономических процессов.
Результаты исследования и их обсуждение
При анализе различных социально-экономических процессов достаточно часто возникает необходимость исследования корреляционной зависимости между экономическими показателями и выявления форм их функциональной зависимости. На современном этапе развития информационных технологий большую роль играет грамотное использование не только существующего математического аппарата, но и применение актуальных цифровых инструментов, осуществляющих автоматизацию трудоемкого процесса выполнения большого объема расчетов. Одним из наиболее часто используемых языков программирования является Python, который в силу своей универсальности, а также наличию специализированных библиотек и пакетов, разработанных для всесторонней обработки данных (Pandas, NumPy и Matplotlib), позволяет строить и анализировать различные модели социально-экономических процессов и явлений.
Рассмотрим анализ взаимосвязи важнейших экономических показателей, характеризующих социально-экономическое положение Центрального федерального округа, такие как валовой региональный продукт (ВРП) (млрд руб.), располагаемые доходы населения ЦФО (руб.), объем инвестиционных вложений в основной капитал (млн руб.), численность малых и средних предприятий региона (тыс.), число занятых в производстве ЦФО (тыс. чел.), оборот малых и средних предприятий (млрд руб.), суммы бюджетных субсидий для интенсификации развития сферы малого и среднего предпринимательства (млрд руб.). В качестве результативного показателя (Y) для проведения исследований была выбрана величина валового регионального продукта (ВРП) (млрд руб.), все остальные показатели рассматривались в качестве факторных признаков (Xi). Таким образом, получим следующий набор переменных:
Y – валовой региональный продукт (ВРП) ЦФО (млрд руб.);
X1 – объем инвестиционных вложений в основной капитал (млн руб.);
Х2 – располагаемые доходы населения ЦФО (руб.);
Х3 – численность малых и средних предприятий округа (тыс.);
Х4 – число занятых в производстве ЦФО (тыс. чел.);
Х5 – оборот малых и средних предприятий ЦФО (млрд руб.);
Х6 – суммы бюджетных субсидий для интенсификации развития сферы малого и среднего предпринимательства (млрд руб.).
Для корректной обработки данных в первую очередь необходимо установить все библиотеки, необходимые для работы с массивами данных:
!pip install pandas numpy matplotlib seaborn statsmodels scikit-learn
Далее осуществляется загрузка файла со статистическими данными, предварительно преобразовав его в датафрейм с использованием соответствующей функции:
df = pd.read_excel(‘/content/drive/ MyDrive/Colab Notebooks/ Экономические показатели РФ.xlsx’)
Проверка корректности загрузки и типы данных осуществлены следующим образом:
df.head(5)
Для возможности дальнейшего анализа временных рядов столбец «Годы» преобразован во временной формат:
df[‘Годы’] = pd.to_datetime(df[‘Годы’])
Расчет основных статистических характеристик исходных данных (среднее значение, стандартное отклонение, границы квартилей) осуществлен, используя коды:
df.describe()
Анализ статистических характеристик показателей помогает оценить однородность и характер распределения исследуемых данных, позволяет сделать предположения о наличии и характере выбросов (аномальных наблюдениях).
Для более качественного анализа статистических данных и построения математических моделей необходимо выполнить загрузку библиотек визуализации. Библиотеки позволяют наглядно представлять результаты однофакторного анализа признаков и делать предположения о наличии и характере связи между признаками.
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
Для оценки силы связи между показателями традиционно осуществляется построение и анализ тепловой карты (матрицы корреляций) признаков (рисунок):
cor_matr = df.corr()
plt.figure(figsize=(8, 6))
sns.heatmap(cor_matr, annot=True, cmap=’coolwarm’, linewidths=0.6)
plt.show()
Анализ матрицы корреляции позволяет выявить факторы, оказывающее наиболее сильное влияние на результативный показатель Y (ВРП субъекта исследования).
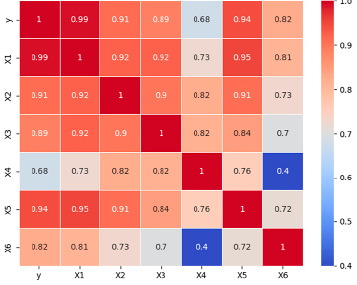
Матрица (тепловая карта) коэффициентов парных корреляций Источник: составлено авторами по [3, 4]
В представленной матрице корреляций практически все анализируемые признаки достаточно тесно связаны с результативным признаком, причем эта связь положительная. Наибольшее влияние на результативный признак Y (ВРП) оказывает фактор-регрессор Х1 «объем инвестиционных вложений в основной капитал», что подтверждается значением коэффициента парной корреляции, равным 0,99. По данным расчетов наименьшее влияние на величину результативного признака Y оказывает фактор-регрессор Х4 «число занятых в производстве ЦФО», что свидетельствует о наличии ряда других факторов, в большей степени определяющих инновационные векторы развития экономики субъекта исследования.
Важным этапом статистического исследования является проверка временных рядов исследуемых показателей на стационарность. Для проверки стационарности временных рядов по каждому показателю воспользуемся соответствующей функцией:
result = adfuller(df[‘y’])
print(‘AD-статистика: %f’ % result[0])
print(‘p-уровень: %f’ % result[1])
for key, value in result[4].items():
print(key, value)
Эта функция позволяет оценить стационарность исследуемых рядов при помощи теста Дики – Фуллера и, в зависимости от полученных показателей (если значение р-уровня меньше заданного уровня значимости), сделать вывод о возможности построения надежных моделей и дальнейшего прогнозирования.
Если первоначальный ряд данных по результатам исследования не является стационарным, то существует возможность его преобразования путем исключения тренда и сезонной компоненты для получения стационарного ряда остатков.
По результатам исследования нестационарными оказались все временные ряды исследуемых показателей, за исключением временных рядов признаков Х4 (численность занятых) и Х6 (суммы бюджетных субсидий).
Для приведения признаков к стационарному виду путем исключения тренда и сезонной составляющей могут быть использованы следующие функции:
df[‘y_без_тренда’] = df[‘y’] – df[‘y’].rolling(window=2).mean()
df[‘y_стационарные’] = df[‘y_без_тренда’].diff()
В результате описанных выше действий исходный датасет был дополнен столбцами «Y_без тренда» и «Y_стационарные», которые могут быть использованы в дальнейшем для более детального анализа исследуемых показателей без учета наличия временного тренда у результативного признака.
Для построения временного ряда, характеризующего изменение результативного показателя во времени, была использована модель ARIMA:
from statsmodels.tsa.arima.model import ARIMA
model1 = ARIMA(df[‘y’], order=(1, 1, 1))
model1_fit = model1.fit()
print(model1_fit.summary())
Фрагмент результатов построения модели ARIMA представлен в табл. 1.
В результате расчетов получено следующее уравнение тренда:
Y(t) = 1 – 0.9854 t + e (t). (1)
Таблица 1
Результаты построения модели ARIMA
================================================================
Dep. Variable: y No. Observations: 17
Model: ARIMA(1, 1, 1) Log Likelihood -157.224
================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------------------------------------------
ar.L1 1.0000 0.003 292.902 0.000 0.993 1.007
ma.L1 -0.9954 0.328 -3.033 0.002 -1.639 -0.352
sigma2 1.806e+07 1.76e-08 1.03e+15 0.000 1.81e+07 1.81e+07
================================================================
Примечание: получено авторами.
Следующим этапом анализа является получение уравнений регрессии результативного признака от каждого факторного признака (построение моделей парных регрессий) и построение уравнения множественной регрессии, позволяющей учесть совместную вариативность всех факторных признаков на результативный признак. Для построения регрессионной модели была выбрана модель OLS() из библиотеки statsmodels.
Построение уравнения регрессии Y (ВРП) от объема инвестиционных вложений в основной капитал (Х1) осуществлено следующим образом:
import statsmodels.api as sm
y = df[‘y’]
x = df[[‘X1’]]
x = sm.add_constant (x)
model2 = sm. OLS (y, x). fit ()
print(model2. summary ())
OLS Regression Results
Результаты построения однофакторной регрессии представлены в табл. 2.
Таким образом, модель парной регрессии показателей Y (ВРП) и X1 (объем инвестиционных вложений в основной капитал) имеет вид
Y (t) = – 0,000114 + 3,3683 X1 (t). (2)
По результатам, представленным в сводке регрессионной статистики, для уравнения однофакторной регрессии p-значение, равное 0,005, меньше табличного значения 0,05, следовательно, построенная модель признается статистически значимой, и можно принять, что Х1 (объем инвестиционных вложений в основной капитал) значимо определяет вариацию и значение результативного признака Y (ВРП ЦФО) [5]. Значение R-квадрата регрессионного уравнения, равное 0,977, свидетельствует о том, что 97,7 % вариации результативного признака может быть объяснено влиянием факторного признака Х1. F-статистика, равная 645,9, свидетельствует об общей статистической значимости построенной регрессионной модели [6, 7].
Таблица 2
Результаты регрессионной статистики однофакторной модели
================================================================
Dep. Variable: y R-squared: 0.977
Model: OLS Adj. R-squared: 0.976
Method: Least Squares F-statistic: 645.9
================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------------------------------------------
const -1.14e+04 3479.036 -3.277 0.005 -1.88e+04 -3983.967
X1 3.3683 0.133 25.414 0.000 3.086 3.651
================================================================
Примечание: получено авторами.
Таблица 3
Сводка многофакторного регрессионного анализа
================================================================
Dep. Variable: y R-squared: 0.984
Model: OLS Adj. R-squared: 0.974
Method: Least Squares F-statistic: 101.9
================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------------------------------------------
const 1.274e+05 1.81e+05 0.704 0.497 -2.76e+05 5.3e+05
X1 3.6840 0.949 3.883 0.003 1.570 5.798
X2 0.0006 0.001 0.680 0.512 -0.001 0.003
X3 -1269.1818 1421.491 -0.893 0.393 -4436.460 1898.097
X4 1.8913 2.709 -0.698 0.501 -7.926 4.144
X5 0.0043 0.330 -0.013 0.990 -0.740 0.731
X6 20.1143 191.075 0.105 0.918 -405.627 445.855
================================================================
Примечание: получено авторами.
Данные характеристики уравнения однофакторной регрессии свидетельствуют о высокой надежности модели и возможности ее использования для целей прогнозирования результативного признака.
Для построения модели множественной регрессии воспользуемся возможностями статистических библиотек:
y = df[‘y’]
x = df[[‘X1’,’X2’,’X3’,’X4’,’X5’, ‘X6’]]
x = sm.add_constant(x)
model3 = sm.OLS(y, x).fit()
print(model3.summary())
В результате получим сводку модели множественной регрессии, фрагмент которой представлен в табл. 3.
Уравнение многофакторной регрессии величины Y (ВРП) от социально-экономических факторов региональной экономики (Х1 – Х6) имеет вид
Y (t) = 1,274e+05+3,684 X1(t)+0,0006 X2(t) –
– 1269,1818 X3(t) + 1,8913 X4(t) +
+ 0,0043X5(t) + 20,1143 X6(t). (3)
Уравнение множественной регрессии признается статистически значимым по критерию Фишера, равному 101,9, и имеет высокий уровень качества, оцениваемый коэффициентом детерминации R-квадрат, равным 0,984. Данные характеристики свидетельствуют о надежном построенном уравнении множественной регрессии, которое с высокой степенью достоверности может быть использовано для разработки прогнозов с целью принятия управленческих решений.
Заключение
Построение математических моделей с использованием современных информационных технологий позволяет автоматизировать трудоемкий и сложный процесс обработки больших массивов статистических данных при проведении научных исследований. Разработанная методика поэтапного построения и анализа массива статистических показателей с использованием многоуровневого языка программирования Рython и специализированных библиотек позволяет создать универсальные формы, которые путем изменения адресации на массивы данных могут быть использованы для анализа различных показателей социально-экономической и смежных сфер деятельности при проведении научных исследований и выработке перспективных планов развития.
Библиографическая ссылка
Березняк И.С., Гусарова О.М., Попова В.В. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ С ИСПОЛЬЗОВАНИЕМ ЦИФРОВЫХ ТЕХНОЛОГИЙ В РЕШЕНИИ ПРИКЛАДНЫХ ЗАДАЧ АНАЛИЗА ДАННЫХ // Современные наукоемкие технологии. 2023. № 12-1. С. 10-15;URL: https://top-technologies.ru/ru/article/view?id=39853 (дата обращения: 05.01.2026).
DOI: https://doi.org/10.17513/snt.39853



