Современные тенденции развития общества требуют от человека быть грамотным. Грамотность составляет основу базовых навыков XXI в. [1]: функциональная грамотность, финансовая грамотность, цифровая грамотность, ИКТ-грамотность, культурная и гражданская грамотность, естественнонаучная грамотность, читательская грамотность, математическая грамотность. Данные навыки есть неотъемлемая составляющая образованности всего общества и основа успешного будущего страны.
Мониторинговая международная программа по оценке образовательных достижений учащихся (Programme for International Student Assessment, PISA), показывает, что уровни сформированности некоторых видов грамотности у российских подростков в возрасте 15 лет за последние 20 лет оказываются недостаточно высокими. Процентное отношение не превышает 50 % от максимального числа баллов (рис. 1) [2].
Приведенная статистика говорит в том числе о недостаточном уровне сформированности у современных российских школьников понимания ценности и значимости математики для решения задач реальной жизни. Большинство из них видят математику лишь как бесконечные формулы и теоремы, оторванные от реальности. Например, как следует из результатов проведенных нами бесед с учащимися, модуль (абсолютная величина) числа для них воспринимается как абстрактное понятие, не связанное ни с одной сферой жизнедеятельности человека, а необходимость умения решать уравнения с модулем на уроках математики – как цель, которая не соответствует задачам действительности.
Это восприятие усугубляется тем, что в школьном курсе математики понятие модуля встречается на протяжении всего обучения в основной и старшей школе при изучении разных учебных тем. Например, в восьмом классе учащиеся сталкиваются с модулем числа при изучении свойств арифметического квадратного корня. В девятом классе при изучении степеней с рациональным показателем также используется понятие модуля числа. На протяжении изучения всей функциональной линии вплоть до конца одиннадцатого класса учащиеся нередко обращаются к понятию модуля числа и его свойствам.
Само понятие модуля (абсолютной величины) числа формируется у учащихся на начальных этапах основной школы, хотя пропедевтика его изучения происходит еще на ступени начальной школы. В шестом классе учащиеся впервые напрямую сталкиваются с понятием модуля числа. В этот период важно следить за правильным формированием этого понятия у учащихся. Неправильно сформированное понятие влечет за собой трудности в его дальнейшем использовании при решении связанных с ним задач. Например, при решении уравнений с модулем, которые встречаются на протяжении всего курса алгебры средней школы.
Овладение учащимися умениями решать уравнения, содержащие переменную под знаком модуля, как правило, является достаточно проблемным для многих учащихся [3]. Причин этому несколько.
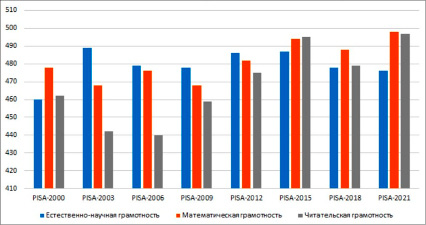
Рис. 1. Результаты России в PISA по 1000-балльной шкале
1. Как было сказано выше, в школьном курсе математики имеет место разброс уравнений с модулем по разным темам в контексте изучения разных видов уравнений: линейных, дробно-рациональных, квадратных, показательных, логарифмических, тригонометрических и др.
2. Неоднозначность раскрытия темы «Модуль числа» в учебниках разных авторов. Например, понятие модуля определяется как расстояние от точки, представляющей число, до начала отсчета (Н.Я. Виленкин), как длина вектора (П.М. Эрдниев), как число «без знака» (Г.В. Дорофеев) и др.
3. В разных учебниках имеют место разные типы задач на применение понятия модуль числа и его свойств, в том числе направленные на обучение учащихся разным методам решения уравнений с модулем.
4. Непонимание учащимися целесообразности изучения уравнений с модулем, практичности использования таких уравнений в реальной жизни.
На основе анализа научно-методической и педагогической литературы один из способов устранения последней причины видится нам в условиях контекстного обучения учащихся. Организация контекстного обучения математике позволяет решать предметные задачи в условиях разного контекста: личного, профессионального, социального и научного (как подразумевает PISA), а также экономического, образовательного и др. Основным средством обучения учащихся в этом случае являются контекстные задачи.
Целью исследования стало определение алгоритма составления контекстных задач по математике и использование в обучении учащихся решению уравнений с модулем контекстных задач, составленных в соответствии с этим алгоритмом.
Материалы и методы исследования
В ходе исследования использовались эмпирические методы (сбор теоретических данных, их сравнение и изучение, беседы с учащимися и учителями) и теоретические методы (анализ и синтез теоретических сведений, абстрагирование от несущественных для данного исследования фактов, идеализация педагогического опыта учителей математики, моделирование). Материалы исследования будут интересны учителям математики и преподавателям педвузов и имеют возможность тиражирования.
Результаты исследования и их обсуждение
Контекст, как основополагающее понятие для контекстной задачи, в научной литературе определяется как «система внутренних и внешних условий жизни и деятельности человека, влияющая на процесс и результаты восприятия, понимания и преобразования человеком конкретной ситуации действия и поступка» [4, с. 124]. Различают два вида контекста:
− внутренний контекст, как индивидуально-психологические особенности, знания и опыт человека;
− внешний контекст, как информационные, предметные, социокультурные, пространственно-временные и иные характеристики ситуации, в которой действует субъект.
В таком случае содержание контекстных задач должно аккумулировать в себе оба вида контекста и потому создавать условия для практической интерпретации результатов, полученных при решении задачи, на языке той или иной сферы жизнедеятельности субъекта с учетом имеющихся у него теоретических знаний.
Отсюда большинством авторов контекстная задача в обучении учащихся определяется как задача, в которой описывается определенная жизненная ситуация, связанная с уже имеющимися знаниями и социокультурным опытом школьников и требующая анализа, осмысления и объяснения учащимся данной ситуации. Результатом решения такой задачи всегда является осознание учащимися личной, профессиональной или общественной значимости некоторой учебной проблемы [5].
В контекстных задачах по математике можно выделить некоторый контекст задания (который представляет собой элементы знакомой обучающимся окружающей среды, такие как общественная жизнь, личная жизнь, образование или профессиональная деятельность, научная деятельность) и собственно математическое содержание (которое включает в себя основные типы математических задач, встречающихся в повседневной жизни: пространственные и плоскостные задачи, задачи на изменение и зависимость, количественные задачи, задачи на работу с данными и др.).
Контекстная задача не является задачей в традиционном понимании. Но в ней также имеют место основные структурные компоненты задачи (условие, требование, решение, базис решения), обладающие своей специфичностью.
Условие контекстной задачи – есть исходные практико-ориентированные факты, сведения, данные и отношения между ними. Фабула контекстной задачи включает в себя описание некоторой практической ситуации, для понимания и разрешения которой необходимо применять знания не только из различных предметных областей (одной или нескольких), но и из повседневного жизненного опыта человека. Такую ситуацию можно охарактеризовать как предметную (ее разрешение требует применения предметных знаний) или как межпредметную (она описывается на языке одной предметной области, но предполагает решение с использованием знаний другой предметной области).
Требование контекстной задачи – получение некоторых практических выводов на основе анализа описываемой ситуации. Предметный смысл требования задачи, как правило, бывает скрыт от решающего. Очевидным он становится только в ходе моделирования указанной ситуации на языке предметной области.
Решение контекстной задачи предполагает интерпретацию описываемой практической ситуации с использованием специального терминологического аппарата той или иной предметной области. Базисом решения контекстной задачи выступают не только предметные знания, умения и навыки решающего, но и его практический, жизненный опыт.
Отличительными признаками контекстной задачи является содержание в ней:
− реальных объектов, с которыми связано описание некоторой реальной ситуации, ее рассмотрение и исследование с обоснованным использованием предметного аппарата и методов;
− разнообразных форм предъявления контекста с целью использования при решении разных механизмов восприятия информации и приемов ее интерпретации;
− непредметных, но познавательных фактов и сведений, которые отражают некоторый аспект жизненной ситуации, доступны для понимания учащимися и мотивируют их на познавательную и исследовательскую деятельность;
− серии обязательных вопросов или заданий, которые помогают учащемуся лучше осмыслить приведенную в тексте информацию, сосредоточиться на конкретных аспектах описанной ситуации и направляют его на правильный путь в решении, а также позволяют увидеть ценность предметной области и ее значимость в реальном мире.
Как показывает проведенный нами анализ научно-методической и учебной литературы, а также интернет-источников, при необходимости использования в обучении контекстной задачи по математике учитель может воспользоваться готовыми ресурсами [6], а может составить такую задачу сам. Некоторыми авторами в своих работах описываются технологии создания контекстных задач (в том числе и обучающимися), а также их корректировки со стороны учителя и решения со стороны учащихся [7; 8]. Наш опыт показывает, что алгоритм составления контекстных задач по математике может быть, к примеру, таким:
1) определить требование (цель) задачи на языке предметной области – математики;
2) перевести требование задачи с языка математики на язык реальной ситуации – для этого определить научный, общественный, учебный, социальный, культурный или иной аспект возможной реальной ситуации, носящий мотивационный и познавательный характер;
3) сформулировать основную цель исследования ситуации в контексте выполнения требования задачи на языке предметной области математики;
4) смоделировать (описать) ситуацию с учетом выбранных одного или нескольких ее аспектов и поставленной цели;
5) добавить вопросы и задания, направленные на более глубокий и расширенный анализ смоделированной ситуации, в том числе с использованием математических методов и приемов.
Приведем пример трансформации традиционной математической задачи 1 по рассматриваемой нами учебной теме «Модуль числа» в контекстную задачу 2 как результат использования приведенного алгоритма.
Задача 1 (математическая). Решите уравнение 2 ∙ |6700 – х| = |х – 4300|.
Задача 2 (контекстная). Иван Иванович и Петр Петрович решили 10 августа отправиться в гости на одну неделю к своему другу Семену Семеновичу, который живет в другом городе. Чтобы осуществить свою поездку, друзья решили воспользоваться услугой каршеринга.
Салон для аренды автомобилей «Автопрокат», куда отправились друзья для выбора автомашины, располагал разными видами транспорта. Цены на аренду легкового автомобиля зависели от его класса – эконом, средний или бизнес. В рамках одного класса цены на разные марки авто тоже разнились. Например, аренда Volkswagen Tiguan составляла 6700 рублей в сутки, а аренда Audi А3 – 4300 рублей в сутки. Посовещавшись, друзья выбрали Skoda Oktavia. Разница между арендой Skoda Oktavia и Volkswagen Tiguan была в 2 раза ниже, чем разница между Skoda Oktavia и Audi А3.
1. Определите, во сколько рублей обойдется друзьям аренда выбранного автомобиля.
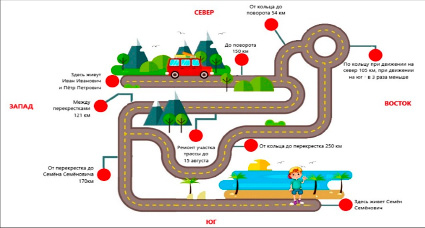
Рис. 2. Схема проезда до города Семена Семеновича
Технические характеристики автомобиля Skoda Oktavia
|
Время разгона, 0–100 км/ч, с |
Мощность, л/с |
Объем топливного бака, л |
Расход топлива л/100 км |
|
8,1 |
150 |
50 |
5,4 |
2. Рассчитайте, сколько километров проедут Иван Иванович и Петр Петрович до Семена Семеновича и обратно, если выберут для поездки кратчайший путь (воспользуйтесь рис. 2).
3. Найдите, сколько литров топлива понадобится друзьям для поездки, если они будут использовать арендованный автомобиль только для того, чтобы добраться до друга и вернуться обратно (воспользуйтесь таблицей).
Представленная контекстная задача 2 не только направлена на развитие у учащихся умения решать уравнения с модулем, в том числе в нестандартной ситуации, но и на формирование у них отдельных навыков XXI в., которые мы указывали выше, – математической грамотности, читательской грамотности и др.
Заключение
Итак, контекстные задачи по математике способствуют привлечению внимания учащихся к учебному предмету и помогают им применять предметные математические знания в реальной жизни, обеспечивая для этого соответствующие условия. Они оказывают влияние на понимание школьниками значимости математики в разрешении практических жизненных ситуаций через их моделирование с использованием математического аппарата.
Контекстные задачи можно составлять по любой теме школьного курса математики. Не исключением является и тема «Модуль числа». В этом случае контекстные задачи способствуют более успешному пониманию учащимися понятия модуль, осознанному осуществлению действий по использованию свойств модуля в решении задач (как математических, так и встречающихся в реальной жизни), а также овладению разными способами решения уравнений с модулем, что особенно важно в подготовке к сдаче ВПР, ОГЭ и ЕГЭ. Использование контекстных задач в обучении учащихся решению уравнений с модулем также позволяет успешно формировать у школьников разные навыки XXI в. и проверять уровень их сформированности.
Для выбора контекстных задач учитель может воспользоваться готовым банком заданий, а может составить их сам, придерживаясь специального алгоритма.
Библиографическая ссылка
Ульянова И.В., Ейкина М.Г., Журавлёва А.А. ПРИМЕНЕНИЕ КОНТЕКСТНЫХ ЗАДАЧ В ОБУЧЕНИИ УЧАЩИХСЯ РЕШЕНИЮ УРАВНЕНИЙ С МОДУЛЕМ // Современные наукоемкие технологии. 2023. № 11. С. 214-219;URL: https://top-technologies.ru/ru/article/view?id=39846 (дата обращения: 17.02.2026).
DOI: https://doi.org/10.17513/snt.39846



