Актуальность теории массового обслуживания и постоянно растущий интерес к совершенствованию ее математического аппарата обусловлены объективными потребностями современного общества, заключающимися в том числе в активизации телекоммуникаций всевозможного характера. Весьма значительное внимание исследователей привлекают немарковские системы. Они используются как модели для описания ряда технических, технологических, экономических объектов. В качестве примеров таких СМО можно привести системы организационного управления, когда влияющая на принятие решений информация имеет ограниченное время актуальности [1, 2]. И хотя теория немарковских систем активно развивается, их моделирование зачастую сталкивается с трудностями, заключающимися, с одной стороны, в затруднительности достаточно полного описания объекта в терминах математической модели, а с другой – в невозможности аналитического решения [3]. Для изучения поведения таких систем применяется аппарат имитационного (алгоритмического) моделирования – способа, максимально соответствующего степени развития современных программных технологий [4].
В данной публикации представлена имитационная модель немарковской системы массового обслуживания с групповым входным потоком заявок, имеющих ограниченное время жизни и обрабатываемых индивидуально в случайные моменты времени. Полагается, что эффективность функционирования системы может быть повышена путем формирования управляющего воздействия, приложенного к ней в некоторый выбранный заранее момент времени. Целью исследования является отыскание этого момента и величины управляющего воздействия, достаточных для достижения желаемого эффекта. Настоящая работа продолжает исследования стационарного случая, опубликованные в статье [5], устраняя вырожденность предыдущего варианта рассмотрением случайного потока обслуживания.
Материалы и методы исследования
Предметом исследования является СМО с групповым входным потоком требований. Заявки имеют ограниченное время жизни, одинаковое для всех элементов потока. Каждое требование обслуживается отдельно в случайный момент времени и имеет одинаковую для всех стоимость обработки. Полагается также, что при средней интенсивности потока обслуживания ниже некоторого значения группа не может быть обработана полностью за указанное время жизни. Количество требований, которое будет обслужено за период, равный времени жизни заявок, будем именовать далее суммарной базовой стоимостью обработки. Ставится задача изучения возможности интенсификации процесса обслуживания, за счет снижения стоимости обработки каждой заявки в отдельности, что позволит обслужить за то же время большее число заявок и обеспечить большую суммарную стоимость по сравнению с базовой.
Для построения модели требуется решить комплекс следующих задач: установить закон распределения случайной величины – времени между моментами обслуживания заявок; определить набор входных параметров, разработать алгоритм имитации потока обслуживания, оценить валидность модели.
Для апробации модели в качестве закона распределения вероятностей случайной величины выбран нормальный закон распределения N(λ, σ2).
В качестве входных параметров модели используются: Q – количество поступивших заявок в составе группы, tend – время жизни заявки, λ – среднее количество времени между моментами обслуживания заявок, σ – среднеквадратичное отклонение, P1 – стоимость обработки каждой заявки, λ2 = f(λ1, P1, P2) – среднее количество времени между моментами облуживания заявок со сниженной стоимостью обработки. Следует отметить, что продолжительность обслуживания в рамках модели не влияет на значение целевой функции – стоимости обработки всех заявок за время их жизни, поэтому не рассматривается как характеристика процесса.
Модельное время определяется моментом прихода группы заявок и временем их жизни и измеряется в минутах. Весь временной диапазон процесса имитации разбивается на интервалы определенной протяженности, которая зависит от значений входных параметров. На каждом из этих интервалов по алгоритму Марсальи генерируются случайные промежутки времени между моментами обслуживания заявок, распределенные по нормальному закону с заданными значениями λ и σ. Сумма обслуженных заявок на всех рабочих интервалах имеет смысл общего количества обработанных требований, которое умножается на стоимость обработки одной заявки, что позволяет получить величину базовой стоимости обработки всех заявок. Входные параметры задаются таким образом, что все заявки группы не могут получить обслуживание до истечения времени жизни.
Модельное время разбивается на два отрезка точкой, в которой реализуется решение об удешевлении стоимости обработки заявки, что в рассматриваемой модели равнозначно интенсификации процесса обработки. Единица измерения момента принятия решения зависит от масштаба характеристик процесса и, как будет показано в дальнейшем, влияет на устойчивость решения. В первый временной отрезок попадают сгенерированные на предыдущем этапе временные интервалы, суммарная длительность которых не превосходит времени принятия решения. На втором временном отрезке генерирование случайных величин происходит заново, с другими параметрами. Очевидно, что возможны различные комбинации входных параметров и разнообразные зависимости λ2 = f(λ1, P1, P2). В примерах, следующих ниже, они будут представлены. Замечание: в рассматриваемой модели, независимо от остальных характеристик процесса, при перестроении функции распределения принято неизменяемым значение коэффициента вариации.
Разработанный алгоритм реализован на языке программирования С#.
Результаты исследования и их обсуждение
Для проведения первого имитационного эксперимента заданы следующие входные параметры:
Q = 1000 штук; tend = 8дней; λ1 = 7.5 минут;
σ1= 1 (2, 3, 4); λ2 = λ1 × (P2 / P1)2; v1 = v2, P1 = 100.
Таблица 1
Лучшие результаты одного эксперимента для зависимости λ2 = λ1 × (P2 / P1)2
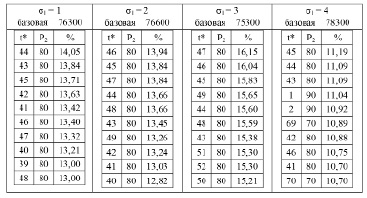
Таблица 2
Результаты 1000 экспериментов для зависимости λ2 = λ1 × (P2 / P1)2
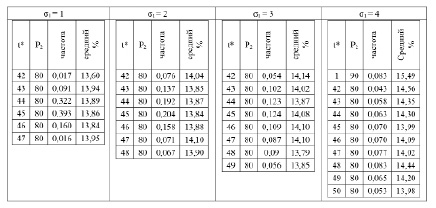
Поиск точки принятия решения осуществляется в часах. Рабочий интервал принят 12-часовым.
Десять лучших результатов одного эксперимента для разных значений σ1 в порядке снижения процента роста базовой суммарной стоимости обработки всех требований представлены в табл. 1. Здесь P2 – стоимость обслуживания заявки после момента времени t* % – процент увеличения базовой суммарной стоимости обработки всех требований.
После проведения 1000 экспериментов для каждого значения σ1 получены результаты, приведенные в табл. 2.
Данные табл. 2 показывают, что однозначно определена величина управляющего воздействия – P2 = 80. А точка принятия решения принадлежит сплошному временному диапазону, локализованному в окрестности момента времени с наивысшей частотой. Определить границы окрестности точки принятия решения позволяет анализ результатов нескольких одиночных опытов. В большинстве решений лучшие пять точек дают процент увеличения базовой суммарной стоимости, отличающийся от максимального не более чем на 0,5 %. Поэтому можно считать, что интервал точек принятия решения определяется моментом времени с наивысшей частотой и радиусом окрестности равным 2. Заметим, что такое решение допустимо и в случае σ1= 4, так как частоты точек (1, 90) и (48, 80) совпадают, но вторая является центром сплошного временного интервала с фиксированной новой стоимостью обслуживания заявки и поэтому является предпочтительней.
Следующий опыт проведен для тех же входных параметров, но другой зависимости:
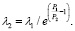
Результаты 1000 опытов для каждого значения σ1 приведены в табл. 3.
Анализируя приведенные результаты, можно сделать вывод, что для σ1 очевидным решением является временной интервал (87, 88). Чтобы убедиться, что для значений среднеквадратичного отклонения, равных 2 и 3, ответ тот же, проведена тысяча экспериментов по выявлению трех лучших точек в каждом опыте. Эти тройки чисел позволяют утверждать, что процент увеличения базовой суммарной стоимости отличается от максимального значения не более чем на 0,5 %. Из материалов таблицы видно также, что для σ1 = 2 в каждой тройке присутствует по крайней мере одна из точек (87, 40), (88, 40), а для σ1 = 3 тройки, не содержащие ни одной из них, составляют 3,2 % от общего числа, что можно интерпретировать как приемлемую статистическую погрешность. В случае σ1 = 4 допущение снижение максимума до 1 % позволяет оперировать уже не тройками, а пятерками лучших значений. В этих условиях уже три точки (87, 40), (88, 40), (89, 40) будут составлять решение задачи, так как частота их появления в результирующих пятерках составляет 95 %.
Считаем важным отметить, что входные параметры для описанных здесь имитационных экспериментов заданы такими же, как и в статье [5], и их результаты, практически полностью совпадают с теми, где функция интенсивности обслуживания заявок была задана аналитически и являлась константой. Это, в свою очередь, свидетельствует о валидности модели и надежности аппарата имитационного моделирования как инструмента ее получения.
Для реализации последнего из представленных в настоящей работе имитационных экспериментов были заданы следующие входные параметры:
Q = 1000 штук; tend = 365 дней;
λ1 = 600 минут; σ1= 100; v1 = v2, P1 = 100000.
Отличительной особенностью этой задачи является порядок входных параметров. После многочисленных опытов удалось установить внутренние характеристики модели, пригодные для получения значимых результатов: снижение стоимости обработки заявки кратно 20000, рабочий интервал (промежуток времени, на котором генерируются интервалы между фактами обработки заявок) составляет 30 дней, поиск решения осуществляется в днях.
В результате 1000 опытов для зависимости λ2 = λ1 × (P2 / P1)2 для всех значений σ1 зафиксирована новая стоимость P2 = 80000. Частоты появления решений в этих опытах изображены на рис. 1.
Таблица 3
Результаты 1000 экспериментов для зависимости 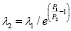
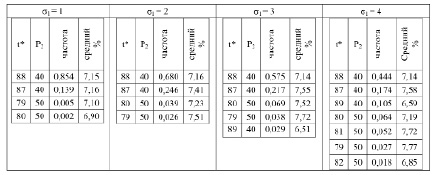
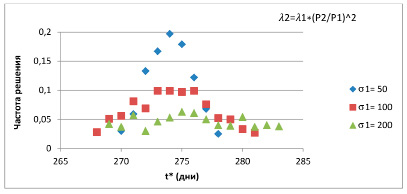
Рис. 1. Частоты появления решений в 1000 опытах для квадратичной зависимости
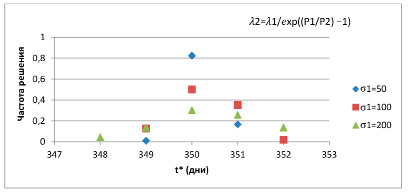
Рис. 2. Частоты появления решений в 1000 опытах для экспоненциальной зависимости
В результате 1000 опытов для зависимости
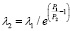
для всех значений σ1 зафиксирована новая стоимость P2 = 40000. Частоты появления решений в этих опытах изображены на рис. 2.
Анализ полученных данных позволяет сделать вывод о том, что, во-первых, более устойчивый результат дает экспоненциальная зависимость, хотя в этом случае средний процент увеличения базовой суммарной стоимости почти в два раза ниже, чем в опытах с квадратичной зависимостью. Во-вторых, локализация точки принятия решения и величина управляющего воздействия в значительной степени определяются видом зависимости и выбором входных параметров. Руководствуясь изложенными выше результатами имитационных экспериментов и их обсуждением, авторы считают, что имеются основания высказать предположение, что в настоящее время указать универсальную процедуру решения подобных задач не представляется возможным. Каждая из них требует индивидуального подхода с обязательным учетом особенностей предметной области.
Заключение
В работе рассмотрена имитационная модель задачи администрирования системы массового обслуживания с групповым входным потоком заявок, имеющих ограниченное время жизни и обрабатываемых индивидуально в случайные моменты времени. Повышение показателя эффективности функционирования системы является целью процесса управления. Для достижения цели построена имитационная модель и проведено большое количество экспериментов с разной комбинацией входных параметров, которыми, в частности, являются вид плотности распределения вероятностей случайной величины, ее характеристики, вид функциональных зависимостей внутренних управляющих величин. В каждом конкретном случае найдены точки приложения управляющего воздействия и его величина, дающие повышение показателя эффективности функционирования СМО. Проведен анализ результатов ряда имитационных экспериментов. Предложено обобщенное решение в виде непрерывного временного интервала, содержащего точку принятия решения, и выбора величины управляющего воздействия на этом промежутке времени для получения результата, наиболее близкого к оптимальному.
Библиографическая ссылка
Шайдуллина Н.К., Печеный Е.А., Нуриев Н.К. МОДЕЛИРОВАНИЕ ПРОЦЕССА АДМИНИСТРИРОВАНИЯ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ЖИЗНИ ЗАЯВОК // Современные наукоемкие технологии. 2023. № 11. С. 81-86;URL: https://top-technologies.ru/ru/article/view?id=39824 (дата обращения: 17.02.2026).
DOI: https://doi.org/10.17513/snt.39824



