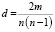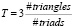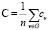В наши дни количество интернет-пользователей стремительно увеличивается. В связи с этим растёт и объем мирового трафика. Согласно прогнозу компании Cisco, в 2023 году число интернет-пользователей превысит отметку в 5 миллиардов. В то же время прогнозируемый объём трафика достигнет отметки в 4.8 зеттабайта [1]. Такой рост активности в Интернете также влечёт за собой увеличение нагрузки на дата-центры. С каждым годом число облачных распределенных вычислительных систем растёт, т.к. крупные компании работают над обеспечением доступности своих продуктов при возникновении высоких нагрузок. Один из способов повышения степени доступности – это использование технологий балансировки нагрузки, что определяет актуальность данной работы. Целью представленного исследования является подход, позволяющий осуществлять балансировку нагрузки распределенной вычислительной системы, представленной графовой моделью, путем разрезания графа на подграфы при помощи алгоритма Кернигана-Лина. Программные системы балансировки нагрузки призваны решить данную проблему, обеспечив качественный доступ пользователей к ресурсам.
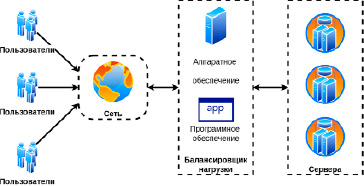
Рис. 1. Общая архитектура балансировщика нагрузки
Балансировщик нагрузки
Процесс балансировки нагрузки заключается в распределении задач между несколькими устройствами (например, серверами [2; 3]) с целью оптимизации использования ресурсов, отказоустойчивости, а также сокращения времени обслуживания запросов [4]. В облачных распределенных вычислительных системах балансировщик нагрузки распределяет нагрузку между узлами сети (облака) [5; 6]. На рисунке 1 представлена общая архитектура балансировщика нагрузки.
Согласно сетевой модели OSI, различные сетевые устройства могут взаимодействовать друг с другом на семи уровнях. В свою очередь, балансировка нагрузки происходит на уровнях 4 и 7: транспортный и прикладной уровни соответственно [7].
На транспортном уровне балансировщик нагрузки занимается отслеживанием сетевой информации о портах и протоколах (UDP и TCP). Доставка трафика происходит при помощи использования ряда алгоритмов балансировки. На прикладном уровне балансировщик нагрузки активно используется в связке с протоколами HTTP/HTTPS. На этом уровне происходит проверка всего трафика [8].
Для улучшения качества доступа используются методы и алгоритмы балансировки нагрузки:
- хэш-подход;
- алгоритм наименьшего времени;
- липкий метод;
- метод наименьшего количества подключений;
- метод циклического перебора.
Представленные алгоритмы определяют наиболее подходящие серверы для приема входящих клиентский запросов.
Целью исследования является экспериментальная проверка возможности балансировки распределенной высоконагруженной системы с использованием алгоритма Кернигана-Лина.
Графовая модель распределенной системы
Программная подсистема балансировки нагрузки должна обрабатывать входную схему сети и представлять её в виде модели графа. В таком случае проблема балансировки рассматривается как задача разрезания графа на подграфы.
Разрезание графа на подграфы – представление исходного графа G = {X,U} в виде множества подграфов, таких что
,
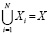где N – количество вершин в исходном графе. Таким образом, все вершины исходного графа должны быть распределены по подграфам. Также следует определить два условия:
‒ 
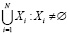: ни один подграф не должен быть пустым;
‒ 
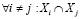: одна и та же вершина не может входить в разные подграфы.
Для задачи разрезания графа не важна структура графа: граф может быть неориентированный или ориентированный, взвешенный или невзвешенный.
Для решения полученной задачи разбиения графа предлагается воспользоваться алгоритмом Кернигана-Лина [9]. Данный алгоритм отлично подходит для обработки взвешенных неориентированных графов. Помимо этого, данный подход позволяет нам напрямую управлять процессом разбиения, оперируя параметром C. Данный параметр отвечает за максимальное количество обменов пар вершин для получения новых вариантов разбиения.
На рисунке 2 представлена схема алгоритма Кернигана-Лина.
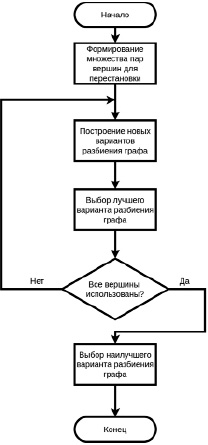
Рис. 2. Схема алгоритма Кернигана-Лина
Алгоритм Кернигана-Лина:
Шаг 1. Формирование множества пар вершин для перестановки. Из незадействованных на данной итерации вершин формируются все возможные пары (при этом в каждой паре должно присутствовать по одной вершине из каждой части имеющегося разбиения).
Шаг 2. Построение новых вариантов разбиения графа. Для получения множества новых вариантов деления производится поочередный обмен пар вершин между частями имеющегося разбиения графа.
Шаг 3. Выбор лучшего варианта разбиения графа. Выбирается лучший вариант среди множества новых делений графа (сформированного на шаге 2). Подходящий вариант далее используется как новое текущее разбиение графа. Соответствующая выбранному варианту пара вершин считается использованной на текущей итерации алгоритма.
Шаг 4. Проверка использования всех вершин. При наличии в графе не использованных вершин (не участвовавших в перестановках) выполнение итерации алгоритма снова продолжается с шага 1. В противном случае, если перебор графа завершен, то следует приступить к шагу 5.
Шаг 5. Выбор наилучшего варианта разбиения графа. Среди всех разбиений графа выбирается наилучший вариант разбиения.
Шаг 6. Конец алгоритма.
Результат работы алгоритма
Для оценки качества разбиения графа необходимо выделить ряд графовых метрик. В таблице представлены метрики для анализа [10].
Метрики оценки качества разбиения графа
|
Метрика |
Формула |
|
Среднее количество внешних рёбер |
- |
|
Средний вес внешних рёбер |
- |
|
Плотность |
|
|
Транзитивность |
|
|
Средний коэффициент кластеризации |
|
|
Обозначения: n – количество узлов, m – количество ребер, #triangles – количество треугольников в графе, #triads – количество триад в графе, cv – коэффициент кластеризации для узла v |
|
Для демонстрации работы алгоритма Кернигана-Лина проведен эксперимент, в ходе которого случайный граф был разрезан на 128 частей. Значение параметра C равно 16 (таким образом, потребуется 16 перестановок пар вершин для определения нового разбиения). Рассматриваемый алгоритм и модель сети были реализованы на языке программирования Python.
Перед проведением эксперимента был выдвинут ряд предположений о качестве полученного разбиения:
- при увеличении количества разбиений количество внешних рёбер уменьшается;
- при увеличении количества разбиений средний вес внешних рёбер уменьшается;
- при увеличении количества разбиений плотность подграфов растёт.
На рисунке 3 продемонстрировано изменение количества внешних связей при увеличении количества разбиений. Исходя из результатов, показанных на рисунке 3, можно сделать вывод о правильности первого предположения о качестве разбиений графа.
Аналогичная ситуация наблюдается и при измерении зависимости среднего веса внешних рёбер от количества разбиений, что наглядно представлено на рисунке 4.
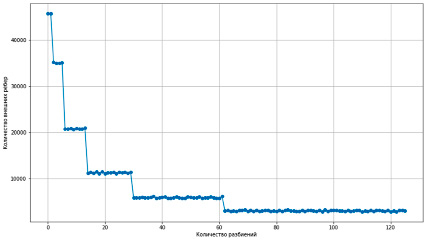
Рис. 3. График зависимости количества внешних связей от количества разбиений
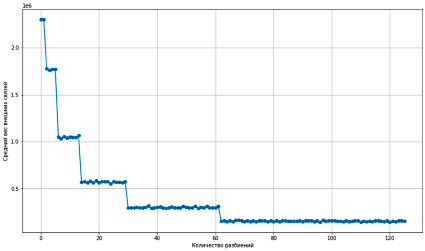
Рис. 4. График зависимости среднего веса внешних рёбер от количества разбиений
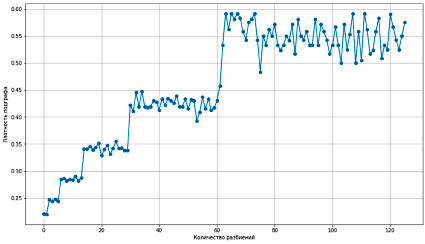
Рис. 5. График зависимости плотности разбиений от количества разбиений
Действительно, при увеличении количества подграфов средний вес внешних связей уменьшается, что и подтверждает второе предположение о качестве разбиения.
Иная картина наблюдается относительно плотности графов. График зависимости плотности разбиений от количества разбиений представлен на рисунке 5.
Исходя из результатов, представленных на рисунке 5, можно судить о том, что средняя плотность подграфов растет пропорционально количеству разбиений.
По результатам эксперимента видно, что алгоритм Кернигана-Лина для разбиения графа позволяет обеспечить качество разбиения, как и ожидалось. Все предположения, выдвинутые перед экспериментом, оказались верны.
Заключение
В работе представлена графовая модель распределенной системы, а также алгоритм, позволяющий решить поставленную задачу разрезания графа.
Предложенный подход позволяет разбить сеть на подсети с учётом представленных ограничений (например, минимальное количество узлов в сети). Также особенностью предложенного подхода является возможность тонкой настройки процесса разбиения при помощи параметра алгоритма Кернигана-Лина. Данный факт позволяет проводить серию разбиений с различными параметрами с целью выявления оптимального разбиения сети на подсети.
Библиографическая ссылка
Трамов И.Б., Ерёмин О.Ю., Степанова М.В., Шульман В.Д. БАЛАНСИРОВКА РАСПРЕДЕЛЕННОЙ ВЫСОКОНАГРУЖЕННОЙ СИСТЕМЫ С ИСПОЛЬЗОВАНИЕМ АЛГОРИТМА КЕРНИГАНА-ЛИНА // Современные наукоемкие технологии. – 2023. – № 11. – С. 62-66;URL: https://top-technologies.ru/ru/article/view?id=39821 (дата обращения: 21.11.2024).