Рассматривается компьютерная обработка последовательности оцифрованных данных биржевых валютных торгов. Для определенности выбраны данные Forex на бирже finam [1]. Котировки скачиваются и сохраняются в файл формата .csv. Файл преобразуется во входную числовую последовательность и отображается в графическом формате. Выполняется сортировка этой последовательности. Используется устойчивая адресная сортировка слиянием по матрицам сравнений [2] (ниже сортировка). Такая сортировка имеет временную сложность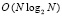 
, в параллельном варианте – 
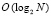, устанавливает взаимно однозначное соответствие входных и выходных индексов сортируемых элементов, что позволяет с единственностью идентифицировать одновременно все локально экстремальные элементы любой числовой последовательности в произвольно фиксированном радиусе локализации [3, 4]. Экстремум идентифицируется по своему значению и местоположению (индексу) во входной последовательности (в одномерном числовом массиве), что приводит к следующей постановке вопроса. Можно ли с помощью сортировки выделить те экстремальные элементы последовательности оцифрованных данных, которые позволяют распознать и идентифицировать динамическое положение целевого объекта, представленного последовательностью? Применительно к данным биржевых (валютных) торгов вопрос сводится к распознаванию тренда и идентификации его разворота. Ниже рассмотрена возможность прогнозирования разворота тренда и его продолжения на краткосрочный период. Аналогично можно ставить вопрос о прогнозировании на среднесрочный и долгосрочный период. Согласно [5] краткосрочный тренд – от нескольких часов до месяца, среднесрочный – от месяца до года, долгосрочный – более года (средняя продолжительность долгосрочного тренда 2–2,5 года).
Цель работы – раскрыть возможности применения сортировки для распознавания и идентификации целевых объектов по информационно существенным локально экстремальным элементам последовательности представляющих их оцифрованных данных. Исследование выполняется на примере последовательности данных валютных торгов. В основу подхода полагается иерархическое выделение из входной последовательности локальных экстремумов, информационно существенно связанных с искомым объектом (в данном случае – с трендом и его разворотом).
Описание метода. Свойства сортировки, включая взаимно однозначное соответствие индексов входных и выходных элементов, детально описаны в [3, 4]. Для представления требуемых свойств и программных механизмов с целью применения непосредственно ниже c незначительной модификацией воспроизводится пример из [3]. Для сокращения текста сортировка слиянием эквивалентно заменена сортировкой подсчетом.
Пример 1. Следующая программа (Delphi) идентифицирует все локально минимальные и локально максимальные элементы массива из раздела описания констант.
program LokMinMaxIII;
{$APPTYPE CONSOLE}
uses
SysUtils;
label 2, 22, 222;
const nn=12;
type vect=array [1..nn] of extended; vect0=array [1..nn] of integer;
const b: vect =
(1.20888884+0.00000000000001, 1.20888884-0.00000000000001, 1.20888884, -6.304, 1.404,
-1.904, 9.504, 1.504, 14.604, 1.704, -11.804, -11.804-0.00000000000001);
var i,k,l,n: integer; a,c: vect; e: vect0;
procedure sort (var n: integer; var a,c: vect; var e: vect0);
var i,j,k: integer;
begin
for i:=1 to n do
begin
k:= 0; for j:=1 to i do
if a[j]<=a[i] then k:=k+1;
for j:=i+1 to n do
if a[j]<a[i] then k:=k+1;
c[k]:=a[i]; e[k]:=i;
end; end;
begin
n:=nn; for i:=1 to n do
a[i]:=b[i]; writeln; writeln; writeln (‘ ‘:6, ‘massiv a’);
for i:=1 to n do
write (‘ ‘:6, a[i]); writeln; writeln; writeln;
sort (n,a,c,e);writeln; writeln; writeln (‘ ‘:6, ‘massiv c’);
for i:=1 to n do
write (‘ ‘:6, c[i]); writeln; writeln; writeln;
writeln (‘ ‘:6, ‘min eps0=1’); writeln; writeln;
k:=1; while k<= n do
begin
for L := 1 to k-1 do if abs(e[k]-e[k- L]) <= 1 then goto 2;
writeln (‘ ‘,c[k],’ ‘,e[k]);
2: k:=k+1;
end; writeln; writeln; writeln (‘ ‘:6, ‘max eps0=1’); writeln;
k:=1; while k<= n do
begin
for L := 1 to n-k do if abs(e[k]-e[k+ L]) <= 1 then goto 22;
writeln (‘ ‘,c[k],’ ‘,e[k]);
22: k:=k+1;
end; writeln; writeln; writeln (‘ ‘:6, ‘min eps0=3’); writeln;
k:=1; while k<= n do
begin
for L := 1 to k-1 do if abs(e[k]-e[k- L]) <= 3 then goto 222;
writeln (‘ ‘,c[k],’ ‘,e[k]);
222: k:=k+1;
end; writeln; writeln; writeln (‘ ‘:6,’podstanovka indeksov’); writeln;
for i:=1 to n do write (‘ ‘:2, ‘ ‘, i); writeln; writeln ;
for i:=1 to n do write (‘ ‘:2, ‘ ‘, e[i]);
readln;
end.
Результат работы программы:
massiv a
1.20888884000001E+0000 1.20888883999999E+0000 1.20888884000000E+0000
-6.30400000000000E+0000 1.40400000000000E+0000 -1.90400000000000E+0000
9.50400000000000E+0000 1.50400000000000E+0000 1.46040000000000E+0001
1.70400000000000E+0000 -1.18040000000000E+0001 -1.18040000000000E+0001
massiv c
-1.18040000000000E+0001 -1.18040000000000E+0001 -6.30400000000000E+0000
-1.90400000000000E+0000 1.20888883999999E+0000 1.20888884000000E+0000
1.20888884000001E+0000 1.40400000000000E+0000 1.50400000000000E+0000
1.70400000000000E+0000 9.50400000000000E+0000 1.46040000000000E+0001
min eps0=1
-1.18040000000000E+0001 12
-6.30400000000000E+0000 4
-1.90400000000000E+0000 6
1.20888883999999E+0000 2
1.50400000000000E+0000 8
max eps0=1
1.20888884000000E+0000 3
1.20888884000001E+0000 1
1.40400000000000E+0000 5
9.50400000000000E+0000 7
1.46040000000000E+0001 9
min eps0=3
-1.18040000000000E+0001 12
-6.30400000000000E+0000 4
podstanovka indeksov
1 2 3 4 5 6 7 8 9 10 11 12
12 11 4 6 2 3 1 5 8 10 7 9
Операторы
k:=1; while k<= n do
begin
for L := 1 to k-1 do if abs(e[k]-e[k- L]) <= eps0 then goto 2; writeln (‘ ‘,c[k],’ ‘,e[k]);
2: k:=k+1; end;
k:=1; while k<= n do
begin
for L := 1 to n-k do if abs(e[k]-e[k+ L]) <=eps00 then goto 22; writeln (‘ ‘,c[k],’ ‘,e[k]);
22: k:=k+1; end;
идентифицируют все локально минимальные элементы (в дальнейшем локальные минимумы) с радиусом локализации eps0 (радиус измеряется числом отсчетов) в цикле по элементам с входным индексом e[k], а также все локально максимальные элементы (в дальнейшем локальные максимумы) в цикле по элементам с входным индексом e[k] с радиусом локализации eps00. Эти операторы (ниже операторы идентификации экстремумов) работают после однократного выполнения сортировки с любым количеством повторений для любого произвольно заданного радиуса локализации. Взаимно однозначное соответствие входных и выходных индексов устанавливается в процессе сортировки операторами c[k]:=a[i]; e[k]:=i. Экстремум идентифицируется по определению. Смысл оператора идентификации в том, что во входном массиве в окрестности радиуса eps0 индекса e[k] отсортированного элемента с[k]=а[e[k]] не должен находиться индекс ни одного меньшего элемента, отсортированного по неубыванию массива, то есть элемента с индексом e[k-L], иначе говоря, элемента с[k-L]=а[e[k-L]]. Аналогично во входном массиве в окрестности радиуса eps00 индекса e[k] отсортированного элемента с[k]=а[e[k]] не должен находиться индекс ни одного большего элемента отсортированного по неубыванию массива, то есть элемента с индексом e[k+L], иначе говоря, элемента с[k+L]=а[e[k+L]]. Отношение «больше» понимается в смысле упорядочения по неубыванию: элемент тем больше, чем больше его номер в отсортированном массиве. В частности, это так для равных элементов, сортировка устойчива и сохраняет их порядок. Аналогично элемент тем меньше, чем меньше его номер в отсортированном массиве. Сортировка сравнивает, но не преобразует элементы, поэтому не вносит погрешность в предложенную идентификацию экстремумов. Очевидно, что не вносит погрешность и операция вычитания индексов. В результате экстремумы идентифицируются алгоритмически и арифметически безошибочно, причем одновременно все для любого фиксированного радиуса локализации. Так, в примере 1 на входе даны элементы 1.20888884+0.00000000000001, 1.20888884-0.00000000000001, 1.20888884, первый и третий из которых идентифицируются как максимумы, второй – как минимум. При этом экстремумы идентифицируются, как отмечалось, по своему значению и своему местоположению (индексу) во входном массиве, в распечатке индекс указан в строке справа от значения. Существенно используемая в дальнейшем особенность идентификации экстремумов заключается в том, что наибольший элемент в окрестности радиуса eps00 идентифицируется как максимум, даже если он расположен в начале или в конце входного массива. Аналогично в конце или в начале массива идентифицируется минимум в окрестности радиуса eps0. В примере 1 максимален первый элемент 1.20888884+0.00000000000001, минимален последний –11.804-0.00000000000001.
В общем случае изложенным способом идентифицируются все экстремумы числового массива
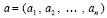(1)
по массиву индексов, полученному после выполнения сортировки массива (1)
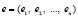, (2)
Условие идентификации максимумов с радиусом локализации ε0 можно представить в виде соотношения [3, 4]
,
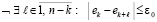означающего, что неравенство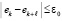 
не должно выполняться ни при одном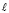 
из отрезка 
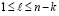. Условие идентификации минимумов имеет вид
, –
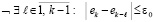неравенство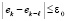 
не должно выполняться ни при одном 
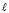из отрезка 
.
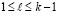Пусть теперь все идентифицированные с некоторым радиусом локализации rmax=eps00 индексы локальных максимумов массива (1) в порядке неубывания во входном массиве обозначены
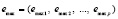, (3)
а все идентифицированные с радиусом локализации rmin=eps0 индексы локальных минимумов этой последовательности в порядке неубывания во входном массиве обозначены
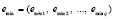. (4)
С помощью (3), (4) (элементы-индексы используются как адреса элементов-значений во входном массиве (1)) формируется новый входной массив для сортировки и идентификации именно на основе индексов экстремумов с некоторым новым радиусом локализации. Процесс формирования нового входного массива из локализованных экстремумов включает, во-первых, запись индексов локальных максимумов (3) и индексов локальных минимумов (4) в один новый массив индексов вида
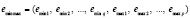;(5)
во-вторых, восстановление исходного порядка следования индексов (по возрастанию) из массива (5) в виде нового массива
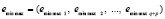; (6)
в-третьих, на основе индексов (6) формируется массив значений экстремальных элементов с данным расположением индексов в массиве (1) (элементы (6) используются как адреса элементов-значений в (1)):
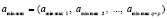. (7)
После преобразований (5)–(7) массив экстремумов (7), расположенных в исходном порядке, принимается за новый входной массив для сортировки и последующей идентификации в нем локальных максимумов (минимумов). Конечная цель таких преобразований – фильтрация экстремумов для выделения существенно информативных максимумов и минимумов последовательности (1). Эту и последующую фильтрацию можно выполнять итерационно до заданного числа повторений количества экстремумов на группе последовательных итераций. Чтобы выделенные экстремумы были существенно информативны в смысле искомой характеристики, в данном случае – в смысле идентификации и разворота тренда, надо применить правильный способ выбора радиуса локализации. Таким образом, имеется в виду следующая конкретная цель рассматриваемых преобразований: она состоит в нахождении радиуса локализации всех существенно информативных экстремумов. Такой способ заимствуется из [6], он использовался также в [7] и заключается в итерационном подходе к выделению экстремумов с автоматизированным программным выбором радиуса локализации. В этом способе за условие остановки последовательных итераций принимается совпадение количества минимумов (максимумов) на каждой из априори заданного количества последовательных итераций. Итерации начинаются с малого значения радиуса локализации, например с rmin = 30. Идентифицируется и запоминается текущее количество минимумов. Затем в исходном массиве (1) с помощью индексов (2) снова идентифицируются минимумы, но уже с увеличенным радиусом локализации, например с rmin = 31, и снова запоминается текущее количество минимумов. При этом радиусы локализации отсчитываются именно относительно входных индексов (2) во входном массиве (1). Процесс итеративно продолжается с увеличением радиуса локализации минимумов на каждой итерации до тех пор, пока не произойдет совпадение количества минимумов, запомненных подряд на нескольких последовательных итерациях. Для рассматриваемого процесса идентификации трендов и их разворотов используются эвристически подобранные для данной предметной области числа последовательных совпадений количества идентифицированных локальных минимумов массива (1). На рассматриваемой стадии преобразований выбрано число итераций с совпадением количества минимумов равное 3. Аналогичный оператор автоматизированного программного подбора радиуса локализации применяется к оператору идентификации локальных максимумов. После достижения априори заданного числа совпадений (в данном случае 3) количества экстремумов итерации останавливаются. На выходе данного применения операторов локализации экстремумов в совокупности с оператором автоматического подбора радиуса локализации получаются значения экстремумов и места (индексы) их расположения во входной последовательности, которые предварительно принимаются за существенно информативные.
Для последующей идентификации трендов и точек разворота тенденций предварительно описанные итерации повторяются с приводимыми ниже конкретными преобразованиями массивов. Именно на первой итерации на вход поступает одномерный массив цены закрытия валютной пары вида (1) с одноминутным таймфреймом. Выполняется его сортировка для получения массива индексов вида (2). Затем выполняется идентификация экстремумов во входном массиве с оператором автоматического программного подбора радиуса локализации. В качестве параметра остановки итераций подбора радиуса выступает трехкратное совпадение количества локальных максимумов (минимумов) на каждой из подряд идущих итераций. В результате получаются массивы индексов вида (3) и (4). В соответствии с последующими преобразованиями полученные результаты обозначаются как
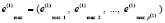(8)
и
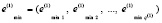(9)
соответственно. Новый входной массив вида (7) обозначается как
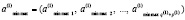.(10)
Далее, относительно (8)–(10) процесс повторяет описанное предварительное выделение существенных экстремумов с той разницей, что имеются три принципиальных отличия. Именно, во-первых, радиус локализации теперь отсчитывается не по индексам входного массива (1), а по индексам сформированного массива (10) (элементы массивов (8), (9) перемещаются в процессе сортировки и используются как адреса идентифицированных элементов входного массива (1)). Во-вторых, начальный радиус в этих итерациях задается равным единице: rmin = 1, rmax = 1. В-третьих, в качестве параметра остановки итераций принимается двукратное совпадение количества локальных максимумов (минимумов) на подряд идущих итерациях. На выходе этого процесса получаются сформированные массивы индексов локальных максимумов
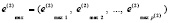(11)
и индексов локальных минимумов
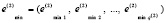, (12)
а также формируется новый входной массив
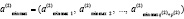.(13)
К массивам (11)–(13) повторно применяется в точности та же, только что описанная, процедура фильтрации с оператором автоматического подбора радиуса локализации (параметр остановки итераций равен 2) локальных максимумов. На выходе получается массив индексов локальных максимумов
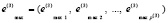(14)
и индексов локальных минимумов
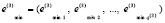, (15)
а также формируются два новых входных массива – массив максимумов
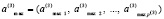(16)
и массив минимумов
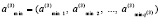. (17)
На этом завершается идентификация существенно информативных экстремумов. На выходе представленных итерационных процессов для дальнейшего анализа и идентификации точек разворота тенденции имеются все требуемые данные: значения и индексы существенно информативных локальных экстремумов входной последовательности (14)–(17). Для идентификации тренда и точек его разворота к полученным массивам (14) и (16) применяется оператор локализации максимумов, но уже без итеративного оператора подбора радиуса локализации. Радиус локализации задается фиксированно, непосредственно равным 2. В результате сформируются массивы, содержащие информацию о направлении и развороте тренда. Именно, массив индексов
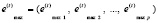(18)
будет содержать точки разворота с подъема тренда на его спуск. Аналогично сформируется массив
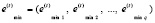, (19)
содержащий точки разворота тренда со спуска на его подъем.
В значениях элементов с индексами (18), (19) спуск от максимума означает нисходящий тренд, подъем от минимума – восходящий тренд. Если такие экстремумы идентифицировались вблизи входного индекса последнего элемента массива (1), они указывают разворот тренда. Если такой экстремум – максимум, тренд развернется вниз. Если такой экстремум – минимум, тренд развернется вверх.
Ниже приводится фрагмент программы определения тренда и разворота на исторических данных биржевых котировок валютных торгов Forex на бирже Finam. Программа написана на языке программирования Python [8], версии 3.10, с использованием дополнительных библиотек: matplotlib [9] – для визуализации результата работы программы; numpy [10] и pandas [11] – для работы с историческими данными котировок, подающимися на вход в файле формата .csv. Во фрагменте программы в роли оператора автоматического подбора радиуса локализации выступает функция coincident(num_iter), которая в качестве параметра принимает число (num_iter) последовательно идентифицированных количеств локальных экстремумов, функции max_extremum(index, eps) и min_extremum(index, eps) выступают в роли операторов идентификации локальных максимумов и минимумов принимают в качестве параметров: массив индексов (index) и значение радиуса локализации (eps) соответственно:
# первый этап
index_1 = merge_arg_sort(close_1)
# остановка подбора радиуса локализации при трехкратном совпадении количества максимумов
max_index_1, max_eps_1 = coincident(3)(max_extremum)(index=index_1, eps=30)
# остановка подбора радиуса локализации при трехкратном совпадении количества минимумов
min_index_1, min_eps_1 = coincident(3)(min_extremum)(index=index_1, eps=30)
# второй этап
index_temp_2 = np.sort(np.hstack((min_index_1, max_index_1)), kind=”mergesort”)
close_2 = close_1[index_temp_2]
index_2 = merge_arg_sort(close_2)
# остановка подбора радиуса локализации при двукратном совпадении количества максимумов
max_index_2, max_eps_2 = coincident(2)(max_extremum)(index=index_2, eps=1)
# остановка подбора радиуса локализации при двукратном совпадении количества минимумов
min_index_2, min_eps_2 = coincident(2)(min_extremum)(index=index_2, eps=1)
# третий этап
index_temp_3 = np.sort(np.hstack((min_index_2, max_index_2)), kind=”mergesort”)
close_3 = close_2[index_temp_3]
index_3 = merge_arg_sort(close_3)
# остановка подбора радиуса локализации при двукратном совпадении количества максимумов
max_index_3, max_eps_3 = coincident(2)(max_extremum)(index=index_3, eps=1)
# остановка подбора радиуса локализации при двукратном совпадении количества минимумов
min_index_3, min_eps_3 = coincident(2)(min_extremum)(index=index_3, eps=1)
# Определение точек разворота тренда (с понижения на подъем)
min_eps_trend = 2
min_index_temp_trend = np.sort(min_index_3, kind=”mergesort”)
min_close_temp_trend = close_3[min_index_temp_trend]
min_index_trend = merge_arg_sort(min_close_temp_trend)
# определение точек разворота тренда с заданным радиусом локализации
min_index_trend_point = min_extremum(index=min_index_trend, eps=min_eps_trend)
min_values_fourth = min_close_temp_trend[min_index_trend_point]
# Определение точек разворота тренда (с подъема на понижение)
max_eps_trend = 2
max_index_temp_trend = np.sort(max_index_3, kind=”mergesort”)
max_close_temp_trend = close_3[max_index_temp_trend]
max_index_trend = merge_arg_sort(max_close_temp_trend)
# определение точек разворота тренда с заданным радиусом локализации
max_index_trend_point = max_extremum(index=max_index_trend, eps=max_eps_trend)
max_values_trend_point = max_close_temp_trend[max_index_trend_point]
Результат работы полной программы графически отображен на рисунке.
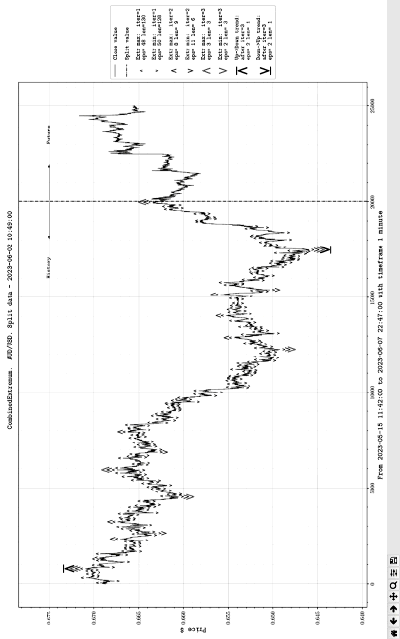
Идентификация трендов и разворотов тенденций
Работа программы соответствует описанному алгоритму. Программа применялась к историческим данным биржевых котировок валютной пары AUD/USD за период с 2023-05-15 11:42 по 2023-06-07 22:47 с таймфреймом равным 1 мин. Для моделирования работы в реальном времени, входные данные разделены на исторические (History) и будущие (Future). На рисунке это разделение обозначено штрихпунктирной вертикалью (Split value), слева от нее исторические, справа – будущие данные. Пояснительная информация отражена на легенде справа от графика. Входные данные цены закрытия валютной пары обозначены непрерывной линией (Close value). На первой итерации идентифицировано 130 существенно информативных максимумов (на графике отмечены символом ˄) с автоматически подобранным радиусом локализации eps=48 и 128 минимумов (на графике отмечены символом ˅) с автоматически подобранным радиусом локализации eps=50. На легенде это отображено соответственно как ˄Extr max: iter = 1 eps = 48, len = 130 и ˅Extr min: iter = 1 eps = 50, len = 128 с соответствующими маркерами. После второй итерации ˄Extr max: iter = 2 eps = 8, len = 9 и ˅Extr min: iter = 2 eps = 11, len = 6 (на графике полученные экстремумы отмечены теми же символами, но большего размера: ˄, ˅). Третья итерация оставила только существенно информативные значения и места расположения в исходном массиве локальных максимумов (минимумов) – ˄Extr max: iter = 3 eps = 3, len = 3 и ˅Extr min: iter = 3 eps = 2, len = 3 (на графике экстремумы отмечены соответственно увеличенными символами ˄ и ˅).
После проведенной фильтрации на выделенных существенно информативных экстремумах (14), (15) и их значениях (16), (17) программно идентифицированы точки разворота тенденций (18) и (19). Разворот с подъема на понижение (на графике отмечен символом ˄) идентифицирован как точка разворота после третьей итерации ˄ Up->Downtrend: after iter = 3 eps = 2 len = 1. Разворот тренда с понижения на подъем (на графике отмечен символом ˅) идентифицирован как точка разворота после третьей итерации ˅ Down->Uptrend: after iter = 3 eps = 2 len = 1.
Результаты исследования и их обсуждение
Согласно рисунку, на краткосрочный период (Future) спрогнозировано продолжение тренда с понижения на подъем. Предложенный метод правильно прогнозирует тренд и точки разворота в целом, с достаточно высокой достоверностью. Подсчет вероятности правильного прогноза является предметом самостоятельного исследования, однако на большом количестве численных экспериментов метод почти всегда дает правильный результат. Его применение целесообразно в случае обработки данных большого числа биржевых котировок. На основании экспериментов метод с большой вероятностью дает достоверные результаты при прогнозировании на среднесрочные и долгосрочные периоды, в этом случае он соответственно модифицируется. В частности, необходимо изменить таймфрейм входных данных. Так, для прогноза на среднесрочный период таймфрейм выбирается равным 15–30 мин, на долгосрочный – от часа до суток. Изложенный подход может иметь значение для оценок сугубо экономического состояния предприятия на основе показаний биржевых торгов акциями предприятия. Если дополнить метод соответственными трактовками конкретной предметной области, то на его основе можно выделять, распознавать и идентифицировать целевые объекты, в частности, по оцифрованной последовательности локационных сигналов. Апробация численных и программных экспериментов в некоторых из данных аспектов представлена в [12, 13], конструктивное применение сортировки для распознавания образов описано в [14, 15].
Заключение
Подход к компьютерной обработке оцифрованных данных биржевых валютных торгов представлен на примере обработки данных Forex на бирже Finam. Устойчивая адресная сортировка одномерного массива данных позволяет с единственностью идентифицировать одновременно все локальные экстремумы с любым радиусом локализации по значению и индексу местоположения. Выделяются наиболее информативные экстремумы, идентифицирующие тренд и его разворот на краткосрочный период. С соответственным видоизменением подход допускает применение сортировки для распознавания и идентификации целевых объектов по существенно информативным локально экстремальным элементам последовательности оцифрованных данных.
Библиографическая ссылка
Ромм Я.Е., Турилин А.С. ИДЕНТИФИКАЦИЯ ТРЕНДОВ БИРЖЕВЫХ КОТИРОВОК НА ОСНОВЕ УСТОЙЧИВОЙ АДРЕСНОЙ СОРТИРОВКИ // Современные наукоемкие технологии. – 2023. – № 11. – С. 52-61;URL: https://top-technologies.ru/ru/article/view?id=39820 (дата обращения: 21.11.2024).