Разработка автоматического управления обогатительной фабрики (ОФ) регламентируется нормативными документами, тем не менее прогнозирование оценки эффективности работы ОФ фактически отсутствует в литературных источниках [1].
Подход к решению повышения производительности мельниц обогатительной фабрики, с внедрением информационно-управляющей системы, при изменении гранулометрического состава питающей руды базируется на нейро-нечетких сетевых моделях и методах оценки параметров технологического процесса измельчения. Автоматизация управления производственным процессом дробления и измельчения руды влияет на снижение себестоимости обработки готового концентрата и потребляемых ресурсов [2, 3].
Одним из эффективных методов исследования для разработки информационно-управляющей системы для управления производственным процессом дробления и возможность спрогнозировать поведение элементов при изменении гранулометрического состава питающей руды является метод дискретного элемента, который применяется для моделирования сложноструктурных породных массивов. Этот численный метод состоит в выявлении взаимосвязи дискретных элементов, взаимодействующих как между собой, так и с составляющими дробительного оборудования, и обеспечивает способность прогноза параметров процесса дробления руды, что важно для формирования математических моделей измельчительного оборудования [4].
В различных исследованиях для разработки прогнозных моделей применялись как стандартные методы математической обработки данных, так и методы интеллектуального анализа данных. Но эти подходы не включают такие важные этапы, как очистка данных, проверка данных на необходимость и возможность их кластеризации, так как они зависят от состава входящей руды, который меняется с течением времени [5, 6].
Актуальность задачи прогнозирования изменения эффективности работы оборудования ОФ при изменении гранулометрического состава входного сырья определяется его значимыми изменениями в случае перехода на разработку нового шельфа и отсутствием в настоящее время полноценных и адекватных методов ее решения.
Технологический процесс измельчения руды – сложная, многофакторная и слабо формализуемая система. Предлагается использовать различные математические модели для прогнозирования изменения производительности мельниц при полноценном анализе изменения гранулометрического состава питающей руды на этапах обработки.
Цель исследования – повышение точности оценки эффективности работы мельниц обогатительной фабрики, используя схему исследования слабоструктурированных производственных данных гранулометрического состава питающей руды.
Материалы и методы исследования
Многокомпонентный подход базируется на применении методов математического статистического, интеллектуального анализа и совокупности предварительно построенных различных прогнозных моделей, дополняющих и верифицирующих друг друга. Подход позволит провести максимально адекватную оценку характера и степени влияния физико-химических характеристик входного сырья на производительность обогатительной фабрики.
Входными показателями прогнозных математических моделей выступают основные технологические показатели, характеризующие гранулометрический состав питающей железной руды. Выходные показатели – оценка ожидаемой производительности мельниц обогатительной фабрики, что позволит повысить качество управления производственным процессом.
В данном исследовании с использованием сформированных имитационных моделей в программе MATLAB R2021a смоделировано изменение производительности мельниц при изменении гранулометрического состава питающей руды на Белгородском ГОКе за 2019–2022 гг. и ожидаемых значений на период 2023 г. [5].
Первоначальный массив данных был представлен основными технологическими показателями, собранными за сутки. Размерность многомерного массива данных 432×28, где 28 соответствует суточным показателям для всех временных периодов 2019–2023 гг., с разбиением в 1 год (4 секции). Для первоначальной обработки и качественного анализа данные были взяты из набора показателей (соответствующих периодам разбиения). Наблюдалось нормальное распределение, и для исключения отклонений были отброшены данные, у которых суммарное время работы всех мельниц соответствовало 95 % от максимально возможного.
Для проведения оценки степени влияния показателей гранулометрического состава питающей руды на производительность с использованием комплексного подхода была сформирована имитационная модель оценки эффективности производительности валковых мельниц обогатительной фабрики. Для этого сформирована суммарная база данных показателей гранулометрического состава входного сырья, рассортированных по временным периодам с 29.12.2019 по 18.01.2022. Период разбиения данных был выбран с учетом требований и равен трем секциям (приблизительно одному году) [6].
Для очистки данных и дальнейшей проверки на возможность их кластеризации, составлен расширенный набора факторов математической модели и построены матрицы корреляций. В соответствии с матрицами корреляций отобраны значения показателей руды с результирующим фактором, имеющим нулевую корреляцию: «Дайка»», «С-актинол», «Класс-0,45» (массовая доля класса «минус 0,045 мм» в концентрате руды).
Используя предсказательные модели: деревья решений Fine, Medium и Сoarse Tree и линейную регрессию, и анализируя среднюю квадратическую величину (σ), выбрали наилучшую точность предсказания (σ = 27,4), что соответствовало линейной регрессионной зависимости. График остатков показан на рис. 1.
Анализ графика остатков линейной регрессии показал, что интервал отклонений данных ± 20 (~ 60 % всех данных), а ± 60 – 3 % данных. Для формирования многофакторной модели регрессоров, 3 % суточных набора данных фактической производительности были отброшены. Поиск адекватного вида математической регрессионной модели и проверка ее на содержание избыточных переменных требовал определить по методу дерева решений с помощью функции plotPredictorImportance характеристики важности показателей руды (рис. 2).
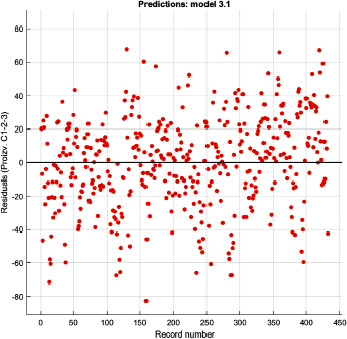
Рис. 1. График остатков линейной регрессии
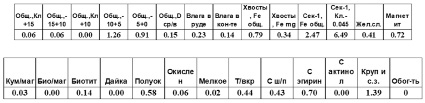
Рис. 2. Показатели многофакторной модели предикторов
Построенная матрица парных корреляций позволила выделить мультикоррелирующие факторы. Посчитанные усредненные оценки значимости были пронормированы по максимальному значению по 100-балльной шкале. На рис. 3 показаны данные усредненных оценок важности факторов по данным периодов 1, 2 и 3.
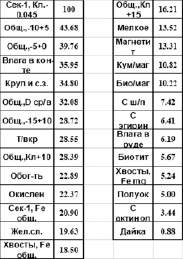
Рис. 3. Усредненная оценка важности факторов
Факторы, имеющие тесную связь, исключены из модели: «Kл+15», «Kл-15+10», «Kл+10», «Kл-5+0», «D с/в», «Магнетит», «Обогатимость», «T/вкр» и факторы, не оказывающие влияния на эффективность: «C эрегин», «Дайка», «Биотит», «Влага в руде», «C ш/п», «C актинол», «Хв. Fe общ», «Полуок». Для поиска наиболее значимых факторов, влияющих на производительность, построена еще одна матрица парных корреляций из сводной базы данных на рис. 4.
После анализа матрицы парных корреляций наиболее значимых факторов из сводной БД были окончательно отобраны наиболее влияющие факторы на регрессионную функцию: «Общ. -5+0», «Влага в кон-те», «Хвосты, Fe общ.», «Сек-1, Кл.-0.045», «Жел.сл.», «Кум/маг», «Био/маг», «Окислен», «Мелкое», «Круп и с.з.».
Исходные данные были разбиты на три секции, но в связи с тем, что у нас однотипный технологический процесс, с целью формирования единой базы данных важно убедиться в однородности массива данных. Метод кластеризации позволил объединить группы данных по однотипной связи, реализованный программными средствами прикладного пакета Matlab методами: «kmeans», с помощью алгоритмов ‘CalinskiHarabasz’ , ‘gap’ (ожидаемое количество классов 1÷10); «gmdistribution», используя алгоритм ‘DaviesBouldin.
Таким образом были выделены семь показателей, влияющих на производительность мельниц обогатительной фабрики при изменении гранулометрического состава питающей руды.
Результаты исследования и их обсуждение
Для формирования имитационной модели прогнозирования изменения в приложении Matlab была разработана программа c функцией Lsqnonlin() (нелинейной аппроксимирующей функцией), с помощью которой построена оптимальная полиномиальная регрессионная модель, найдены доверительные области, в окрестности значений единицы, которые в большей степени удовлетворяют искомой степени факторов и их регрессионным коэффициентам для минимизации среднеквадратичной разности фактических и прогнозных значений.
Оптимальная полиноминальная регрессионная модель:
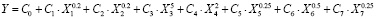 (1)
(1)
где Y – это результирующий фактор, т.е. производительность в т/час;
1 – «Кл Общ.,-5+0», X2 – «Хвосты, Fe общ.», X3 – «Окислен», X4 – «Мелкое», X5 – «Круп и с.з.», X6 – «Сек-1, Кл.-0.045», X7 – «Кум/маг».
С учетом стремления к росту степеней факторов X6 , X7 и малой значимости коэффициента перед фактором «Кум/маг» была сформирована следующая оптимальная регрессионная модель:
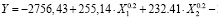
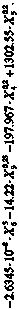 (2)
(2)
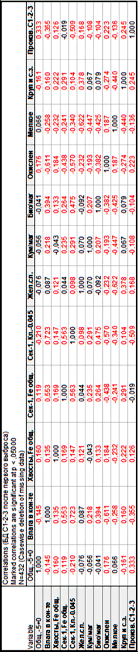
Рис. 4. Матрица парных корреляций наиболее значимых факторов из сводной БД
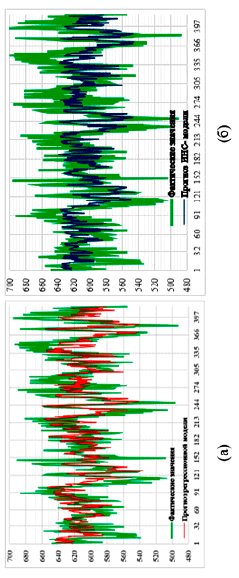
Рис. 5. Графики среднесуточных значений (фактические и прогнозные) производительности, полученных по регрессионной модели (а), по ИНС-модели (б)
Данная зависимость имеет следующие показатели качества: множественный коэффициент корреляции R – 0,67, коэффициент детерминации R2 – 0,454; нормированный R2 – 0,443; стандартная ошибка – 27,26. Среднее абсолютное отклонение прогноза этой модели от фактических значений составляет 21,34, что в пределах статистической ошибки не отличается от значения этого показателя для предыдущей модели, включающей семь факторов.
Таким образом, можно заключить, что построенная модель является оптимальной, ее показатели практически не отличаются от модели, включающей в себя еще фактор «Кум/маг», значимость которого не влияет на достоверность адекватности модели. В связи с этим предлагается применять в равной степени модель (1) и модель (2).
С целью визуализации полученных результатов проведена верификация качества построенной прогнозной модели искусственной нейронной сети (ИНС), сформированы графики, показанные на рис. 5.
Регрессионная и ИНС-модели показывают схожую динамику изменения величины показателя прогнозирования производительности при соответствующих изменениях значений показателей, входящих в суточный набор данных, входящих в суммарную базу данных.
Таким образом, при нахождении среднего фактического значения в диапазоне от 560 до 650 т/ч точность прогнозирования изменения производительности мельниц обогатительной фабрики при изменении гранулометрического состава питающей руды выше в ±8 %.
Коэффициент R2 = 0,45 при адекватности регрессионной модели показывает, что на изменение результирующего показателя значимое влияние оказывают неучтенные в прогнозной модели факторы за короткий период (сутки). Поэтому целесообразно использовать для прогнозирования средних значений производительности за более длительный период.
Заключение
В результате исследования сформирован многокомпонентный подход решения проблемы оценивания ожидаемой производительности мельниц обогатительной фабрики при изменении гранулометрического состава питающей руды. Схема исследования, построенная с использованием математических и интеллектуальных методов анализа и применением различных дополняющих и верифицирующих друг друга прогнозных моделей, показала свою эффективность, а уровень достоверности полученных с ее помощью результатов позволяет ее использовать для оценки ожидаемых изменений искомого показателя при вариации входных параметров.
Библиографическая ссылка
Иващук О.Д., Федоров В.И., Игрунова С.В., Нестерова Е.В., Константинов И.С., Иващук О.О., Удовенко И.В. ПРОГНОЗИРОВАНИЕ ИЗМЕНЕНИЯ ПРОИЗВОДИТЕЛЬНОСТИ МЕЛЬНИЦ ОБОГАТИТЕЛЬНОЙ ФАБРИКИ ПРИ ИЗМЕНЕНИИ ГРАНУЛОМЕТРИЧЕСКОГО СОСТАВА ПИТАЮЩЕЙ РУДЫ // Современные наукоемкие технологии. 2023. № 11. С. 33-38;URL: https://top-technologies.ru/ru/article/view?id=39817 (дата обращения: 17.02.2026).
DOI: https://doi.org/10.17513/snt.39817



