Современное развитие цифрового телевидения и киноиндустрии приводит к серьезному росту объема видеосигналов, связанных во многом с повышением качества передаваемого изображения и усложнением содержания самого сигнала с точки зрения его обработки и трансляции. В результате до сих пор остается актуальной проблема разработки математической модели обработки, очистки и сжатия такого рода сигналов при обязательном требовании сохранения качества транслируемой видеоинформации. В настоящее время представлены различные методы сжатия и обработки видеосигналов, основанные на многообразных математических базах, таких как ряды Фурье, вейвлеты и фракталы. Наибольший интерес представляют методы, использующие современную математическую основу, базирующуюся на применении вейвлетов и фракталов. Формирование математической модели обработки сигнала позволяет создавать универсальную систему работы с различными видами радиосигналов независимо от их сложности построения и содержания передаваемой информации. Правильно выбранный математический аппарат формирует простоту и удобство обработки различных сигналов в зависимости от особенностей постановки конкретной задачи. Современные системы передачи сигналов требуют разработки математических моделей анализа и обработки цифровых и детерминированных дискретных сигналов. Наибольший интерес на данном этапе развития представляет модель предиктивного сжатия сигналов с регулированием шага кодирования. В предыдущей работе [1] авторами была представлена и апробирована на конкретных сигналах одна из возможных математических моделей такого метода сжатия, продемонстрировавшая достаточно приемлемые результаты. Данная модель базируется на рекурсивном способе сжатия, при котором предсказание и выбор шага сжатия определялись интегральной зависимостью накапливаемой погрешности обработки сигнала. Анализ методов лифтинговой схемы продемонстрировал возможность уменьшения количества базисных коэффициентов сжатия при возможности сохранения качества информации на основе применения вейвлетов второго поколения. Таким образом, использование данной схемы позволит улучшить качество подбора шага сжатия, тем самым обеспечивая более высокий уровень уменьшения объема данных при сохранении качества исследуемого сигнала.
Цель исследования – улучшение модели предиктивного метода обработки и сжатия различных радиосигналов на основе модификации лифтинговой схемы, обеспечивающей увеличение шага сжатия с целью уменьшения объема занимаемой информации при сохранении основных параметров сигнала.
Материалы и методы исследования
Рекурсивные методы задания дискретных сигналов, представленные в [1], естественным образом связаны с лифтинговой схемой сжатия сигналов и конструированием так называемых вейвлетов второго поколения, обладающих рядом дополнительных по отношению к вейвлетам первого поколения полезных свойств. Одна из отличительных особенностей вейвлетов второго поколения состоит в том, что формальное их описание, так же как и описание рекурсивных методов представления дискретных сигналов, проводится во временной области.
Поясним связь лифтинговой схемы сжатия с предиктивными методами представления дискретных сигналов. Лифтинговая схема базируется на итерационной процедуре усечения исходной выборки. Составляющим этапом такой процедуры является рекурсивное восстановление «пропущенных» отсчетов, основанное на аппроксимации функции-сигнала, заданной в узлах [2].
В предиктивных методах обычно применяют кусочно-линейную экстраполяцию. В этом случае на каждой итерации проводится оперативное (in-place) вычисление i-отсчета по значениям предыдущих отсчетов с номерами (i – 2) и (i – 1). Однако и в лифтинговой схеме на каждом шаге декомпозиции сигнала при уменьшении вдвое числа отсчетов некоторой исходной выборки используется полиномиальная интерполяция, в простейшем случае – также кусочно-линейная.
Общей задачей лифтинговой схемы является «декорреляция» исходного сигнала, т.е. представление сигнала меньшим числом отсчетов, что эквивалентно увеличению интервала дискретизации. При этом необходимо контролировать точность аппроксимации, сопоставляя эту точность с допустимой мерой погрешности. Естественно, что при этом желательно использовать такие аппроксимирующие процедуры, которые снижают ошибку приближения, не увеличивая при этом в значительной степени количества вычислительных операций.
Пусть задана выборка {xij}, где i = 0,1,2… – номер отсчета, j = 0, –1, –2… – номер шага в лифтинговой схеме. Первый индекс пересчитывает шаги декомпозиции, так, что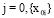 
соответствует исходной выборке, а 
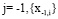– следующему шагу декомпозиции сигнала. После этапа разбиения исходной выборки число отсчетов уменьшается вдвое, при этом остаются только четные отсчеты 
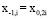. Преобразование, в процессе которого исходная выборка {x0i} декоррелируется путем расщепления на четные и нечетные отсчеты, порождает вейвлеты Лейзи (Lazy wavelet).
Лифтинговая схема преобразования сигнала, согласно рисунку 1, включает в себя три части: разбиение (S), предсказание (P) и обновление (U). Поскольку собственно лифтинговая схема достаточно подробно обсуждается в оригинальных работах [3, 4], далее здесь приводится только описание модификации этапа предсказания. Предлагаемая в данном исследовании модификация (P)-этапа традиционной лифтинговой схемы основана на применении полиномов Бесселя, которые не являются интерполяционными в строгом смысле, но позволяют повысить точность аппроксимации по сравнению с обычной кусочно-квадратичной интерполяцией.
Для получения обратимого компактного представления выборки необходимо построить процедуру восстановления «пропущенных» нечетных отсчетов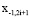 
. Самый простой вариант такого восстановления – кусочно-линейная интерполяция по «оставшимся» четным отсчетам-узлам. Такая кусочно-линейная интерполяция проводится по формулам, приведенным для адаптивного предсказания в предыдущем нашем исследовании [1]. Повысить точность восстановления пропущенного отсчета можно с помощью интерполирования движущимся полиномом Pm фиксированной степени выше первой m > 1. Однако при этом нецелесообразно стремиться к дальнейшему увеличению степени интерполяционного полинома, устанавливая, например, m > 3.
Разумным выбором для аппроксимации сигнала на интервале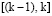 
является использование интерполяционных полиномов второй степени m = 2, симметрично скомбинированных в полином Бесселя:
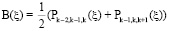, (1)
где
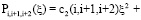
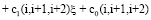
индексы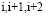 
соответствуют номерам левых и правых симметричных узлов (отсчетов), ближайших к обрабатываемому интервалу 
: 
.
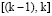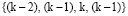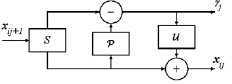
Рис. 1. Лифтинговая схема преобразования сигнала во временной области; xj+1,i – исходная выборка, xj,i – прореженная выборка (один шаг декомпозиции сигнала), yj – коэффициенты компактного представления сигнала (вейвлет-коэффициенты)
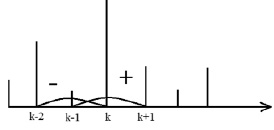
Рис. 2. Расположение узлов для обработки отсчетов на интервале [(k–1),k] при использовании полинома Бесселя второго порядка. Знаком (–) обозначена тройка левых узлов {(k – 2), (k – 1), k}; знаком (+) обозначена тройка правых узлов {(k – 1), k, (k+1)}
На рисунке 2 показано расположение узлов для построения полинома Бесселя второго порядка, аппроксимирующего отсчет в интервале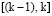 
.
Строго говоря, полином Бесселя не является интерполяционным, поскольку в нашем случае имеет второй порядок m = 2, использует 4 узла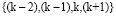 
и при этом совпадает с исходными отсчетами только в двух точках, соответствующих номерам отсчетов (k – 1) и k. Благодаря симметричному относительно отрезка 
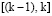расположению узлов 
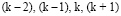погрешность приближения оказывается меньше, чем в случае простой квадратичной интерполяции. В [4] приведена следующая оценка погрешности для полинома Бесселя второго порядка
,
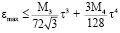где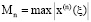 
.
При обработке граничных интервалов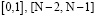 
сигнала длины N следует использовать не полином Бесселя, а обычные интерполяционные полиномы второго порядка [5], построенные по ближайшим к границам узлам {0,1,2} и 
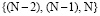. При обработке внутренних интервалов 
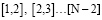следует использовать полином Бесселя. Коэффициенты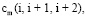 
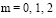
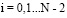интерполяционных полиномов, формирующих полином Бесселя, определяются по стандартным алгоритмам.
Различные степени аппроксимации исходного сигнала могут быть достигнуты, если при реконструкции сигнала использовать не весь набор вейвлет-коэффициентов dj,k, а всего лишь часть их, опуская маленькие коэффициенты, не превышающие некоторого заданного порогового значения ε.
Такое ограничение набора вейвлет-коэффициентов позволяет решать три задачи: экономить вычислительные ресурсы, обеспечить сжатие сигнала, очистить сигнал от шумов. Если суммирование ведется только по коэффициентам |dj,k| > ε и число отброшенных коэффициентов равно n0, то аппроксимирующая функция fε отличается по норме от исходного сигнала f(x) следующим образом:
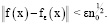(2)
Для гладкого сигнала, существенно изменяющегося только на очень малых интервалах, большое число вейвлет-коэффициентов мало, и потому можно выбирать малые пороговые значения ε при сохранении высокой точности в аппроксимации f(x).
Вместо этой процедуры – так называемого жесткого сжатия – иногда используют пороги с мягким сжатием, когда после выбрасывания всех коэффициентов, не достигших порога по своему абсолютному значению, сдвигают все оставшиеся коэффициенты к их общему началу, т.е. заменяют все невыброшенные dj,k на значения
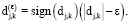(3)
Данный подход приводит к оптимальным оценкам. Коэффициенты разложения определяются с помощью быстрого вейвлет-преобразования, поскольку коэффициенты s0,k заданы дискретными значениями f(x). Однако в итерационных схемах ошибка накапливается, и точность может оказаться недостаточной. Намного лучшей точности удается добиться с использованием интерполяционных вейвлетов. В этом случае значения функции на однородной решетке f(k) принимаются за s-коэффициенты для интерполяционного базиса, а начальные значения s0,k находятся в виде некоторых их линейных комбинаций, коэффициенты в которых определяются из решения уравнений, зависящих от вида выбранных вейвлетов.
Результаты исследования и их обсуждение
Применение полиномов Бесселя и вейвлетов второго порядка для оценки накопленной ошибки шага рекурсивной экстраполяции сигнала позволило существенно улучшить методику оценки данной ошибки, тем самым дало возможность увеличить шаг сжатия при сохранении качества сигнала и уменьшении объема занимаемой информации. Наличие в сигнале шума существенно усложняет модель обработки и сжатия сигнала, что увеличивает погрешность сжатия, приводящую к уменьшению интервала шага и тем самым – к росту объема данных. Применение полиномов Бесселя и вейвлетов второго порядка позволило повысить точность экстраполяции и уменьшить накопленную ошибку, что продемонстрировано на рисунке 3.
Разработанная модель продемонстрировала существенное уменьшение накопленной погрешности сжатия и отсутствие зависимости ошибки от зашумленности сигнала, что видно на изображении третьей зависимости на графике. Вместе с тем очень часто нельзя с уверенностью предполагать аддитивный характер шума.
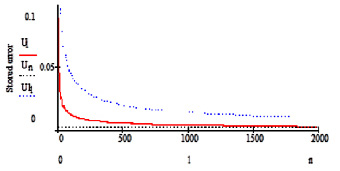
Рис. 3. Зависимость накопленной ошибки в зависимости от метода сжатия сигнала
В таком случае эффективность методов пороговой очистки сигнала, а по существу – методов вейвлет-аппроксимации сигнала, базирующихся на основной модели аддитивного шума, оказывается под вопросом. И первой задачей, которую следует решить в процессе разработки критериев пороговой очистки сигнала с мультипликативными шумами, является корректное сравнение эффективности очистки сигнала с аддитивным шумом и сигнала с мультипликативными шумами. Предложенная модель выбора шага обработки показала ее существенную независимость от вида шума, что позволяет применять данную модель при наличии в сигналах шумов разной природы.
Выводы
1. Произведена модернизация алгоритма пошагового предсказания на основе использования полиномов Бесселя и вейвлетов второго порядка, что позволило уменьшить погрешность выбора шага кодирования. Данная модернизация дала возможность обеспечить сжатие сигналов с улучшенным качеством содержания при уменьшении физического объема данных.
2. Разработанная модернизация пошаговой рекурсии сигнала создала систему улучшения выбора шага обработки сигнала, исключающую зависимость накопленной ошибки от вида сигнала и природы шумов в радиосигналах, что существенно повышает эффективность алгоритма предиктивного сжатия сигналов с регулированием шага кодирования.
Библиографическая ссылка
Андреев К.В., Быков А.А., Михалёв А.С. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МОДИФИКАЦИИ ЛИФТИНГОВОЙ СХЕМЫ РЕКУРСИВНОГО ПРЕДСТАВЛЕНИЯ РАДИОСИГНАЛОВ НА ОСНОВЕ ВЕЙВЛЕТОВ ВТОРОГО ПОКОЛЕНИЯ // Современные наукоемкие технологии. – 2023. – № 11. – С. 16-20;URL: https://top-technologies.ru/ru/article/view?id=39814 (дата обращения: 20.05.2024).